本文主要是介绍一场椭圆曲线的寻根问祖之旅 | FISCO BCOS密码学探究,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

本文介绍密码学中常见的椭圆曲线以及他们之间的关系,介绍不同标准体系的命名规则,尝试描述椭圆曲线之间的家族演义关系。文章试图讲清椭圆曲线相关概念和功能,不涉及复杂的数学证明和推理,欢迎感兴趣的同学阅读。笔者主要参考Wikipedia和相关组织网站的信息进行整理,不排除出现纰漏的可能,欢迎专家批评指正。
一个可能你没关心过的问题
在《一个数字引发的探索——ECDSA解析》(加链接)中提到一个椭圆曲线secp256k1,它有一些特性,可以快速计算出recoveryID。
这个secp256k1为什么如此命名?
不怕各位笑话,我在弄清楚它之前,经常拼写错,写成sec256pk1,seck256p1等😅
咬文嚼字secp256k1
搞清楚secp256k1的命名含义其实很简单,搜索引擎可以快速为你定位到答案,它出自一个密码协议标准,每一个字母和数字都代表着特定含义,我们来逐一解析。

(1)密码协议标准
第一部分是「sec」,sec是Standards for Efficient Cryptography 的简称,是SECG发布的一种密码学协议标准。
SECG发布的「SEC 1」和「SEC 2」两个关于椭圆曲线的协议标准,在「SEC 2」中有详细说明secp256k1以及其他曲线的参数定义。
除了「sec」,还有众多其他关于椭圆曲线的协议标准,从「SafeCurve」中可以看到有下列不同类型的标准。

「SafeCurve」此处较久没有更新,有些标准已经更新了多次,例如NIST关于数字签名的标准 FIPS 186目前在用的是第四版,第五版也在起草中了,从「NIST」官网中可见。
NIST是美国的国家标准技术研究所(National Institute of Standards and Technology),因此,NIST的标准也是美国标准。

「NIST FIPS 186-4」标准中定义了若干椭圆曲线标准,例如NIST P-256、NIST P-384等,其中开头NIST也代表密码协议标准的名字。后续描述都是围绕这两个标准来解析。
(2)有限域
第二部分是「p」,p表示该椭圆曲线是基于素数有限域Fp。有限域是离散数学中的概念,此处不做展开,简单来说,它是一个由有限数量元素组成的集合,元素之间可以进行加法和乘法计算,具备一些独特的属性。
密码学中使用椭圆曲线都是基于有限域的,除了素数有限域Fp之外,还有另一种特征为2的有限域F2m (因输入格式问题,全文2m应为2的m次方,下同),Fp的大小(元素个数)为p,F2m的大小为2m。
基于Fp的椭圆曲线为:

基于F2m的椭圆曲线为:
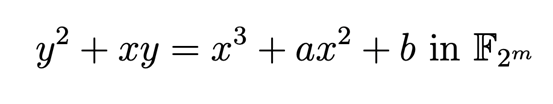
在「SEC 2」中还定义了sect163k1、sect163r1等曲线,其中,t表示的是该曲线基于F2m。在「NIST FIPS 186-4」中定了P-256、B-163等曲线,P-表示基于Fp,B-表示基于F2m。
(3)有限域大小
每个椭圆曲线E都有若干关键参数,包括阶为n的基点G和系数h等,其中,n为一个大素数,n*h为椭圆曲线上点的数量。为了计算效率考虑,h通常设置为1、2或4。
通俗地讲,如果椭圆曲线上的点数量越多,那么这条椭圆曲线的安全度就越高,因此n的取值是影响曲线安全的关键。
椭圆曲线又都是基于有限域的,曲线上的点都是有限域中的元素,因此,有限域大小决定了曲线安全度。
第三部分「256」就是有限域大小的表现形式,还有更多其他如192、224、384等,在「NIST FIPS 186-4」中有个表格展现了Fp 和F2m两个域的各种不同大小配置。

SEC标准在这块的设置和NIST标准类似,我们会看到p系列的曲线有p192、p224、p256(secp256k1就是其中一种)、p384和p521,t/B系列有t163/B-163、t233/B-233等。
(4)Koblitz Curve
第四部分「k」表示该曲线是Koblitz Curve,从「SEC 2」中可以看到还有此处标记为r的曲线(如secp256r1),r表示该曲线是伪随机曲线Pesudo-Random Curve。
Koblitz Curve命名源自数学家「Neal Koblitz」,它是一种特殊的曲线,它的一些参数是精心挑选设置的。Koblitz Curve具有自同态的性质,可以通过优化大幅提升计算效率。
相比之下,Pesudo-Random Curve的对应参数是通过随机种子计算出来的,有标准的检验算法可以检测所有参数是随机种子产生而来。
对应「(2)有限域」中的两个椭圆曲线,Koblitz Curve分别简化为


例如,secp256k1对应的曲线b=7,即曲线表示为

在「NIST FIPS 186-4」中Koblitz Curve曲线以「K-」标记开头,分别有K-163、K-233等。
(5)末位标记
到了第五部分「1」,这是代表在前4个条件下提供了多种推荐参数设置,在SEC标准中大部分该位都是1,即只提供一种推荐参数,sect163r2是一个例外。
下面把SEC和NIST两个标准推荐的曲线分别列一下,二者有较大部分是相同的参数设置。
| SEC | NIST |
| secp192r1 | P-192 |
| secp224r1 | P-224 |
| secp256r1 | P-256 |
| secp384r1 | P-384 |
| secp521r1 | P-521 |
| secp192k1 | |
| secp224k1 | |
| secp256k1 | |
| sect163k1 | K-163 |
| sect163r1 | |
| sect163r2 | B-163 |
| sect233k1 | K-233 |
| sect233r1 | B-233 |
| sect239k1 | |
| sect283k1 | K-283 |
| sect283r1 | B-283 |
| sect409k1 | K-409 |
| sect409r1 | B-409 |
| sect571k1 | K-571 |
| sect571r1 | B-571 |
上述表格中,同一行中SEC和NIST都出现的,两个曲线虽然名字不同,但参数完全相同,也就是说其实一样的。
橙色底纹的几个SEC曲线没有对应的NIST曲线,因此SEC标准包含的曲线比NIST多一些,本文开头提到的secp256k1就是SEC单独存在的。
说到这里,不得不提一个正经八卦。据说,NIST推荐的Pesudo-Random Curve,也就是P和B系列,并没有公布随机数挑选规则,外界存在一种疑虑,可能NSA(美国国家安全局)掌握了后门,能够轻易破解这些密码协议。有兴趣的同学可以搜索「Dual_EC_DRBG后门」,更大的八卦是据说中本聪选择secp256k1作为比特币签名算法的曲线,而没有选择更常用的secp256r1,也是因为这个潜藏的风险。
椭圆曲线族谱
调研发现,「Standard curve database」记录了比「SafeCurve」更为详细的标准和曲线,感觉这可以算是椭圆曲线族谱了。翻阅该网站记录的所有曲线,发现绝大部分还是基于「(2)有限域」中的曲线,推荐的参数不同而已。
但是,在「other」中存在几种例外,E-222采用Edward Curve,Curve25519采用Montgomery Curve,Ed448采用Twisted Edward Curve。
Edward Curve是什么?Montgomery Curve又是怎样的?Edward与Twisted Edward Curve又有什么关系?
上述问题再一次触碰到我的知识盲区,所以接下来只好以截图为主,内容源自Wikipedia,如果觉得看着有点晕,可直接跳过看结论。
「Edward Curve」定义如下:

「Montgomery Curve」定义如下:

「Twisted Edward Curve」定义如下:

「Curve25519」定义如下:

「Ed25519」的定义如下:
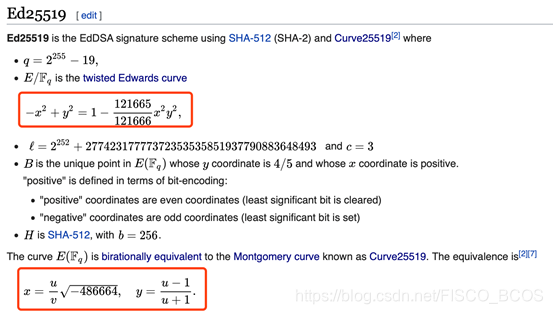
根据Wikipedia,大概可以整理出这么几个信息:
- Edward Curve是Twisted Edward Curve中的一种
- Twisted Edward Curve和Montgomery Curve可以互相转换
- Edward Curve和Montgomery Curve这两种曲线都具有特殊属性,例如能够为计算加速
- Curve25519是一种曲线,Ed25519是一种签名算法
- Curve25519又是精选的Montgomery Curve,具有更高的计算效率
- Curve25519和Ed25519采用的曲线是一致的,一个是Montgomery表现形式,一个是Twisted Edward Curve表现形式
- 25519的取名来自于该曲线的有限域参数p=2255-19
在阅读Wikipedia的过程中发现一个名字「Weierstrass equation」,原来它才是这些曲线的鼻祖,在一个域k上的任何一个平面曲线,都可以表示成Weierstrass equation。
![]()
不难发现,前面提到过的各个公式都是Weierstrass equation的一种演化版本(Twisted Edward Curve看起来不是,但是它可以转换到Montgomery Curve,本质上也一样)
到此,为椭圆曲线寻根问到祖,并且从「STD」也获知了椭圆曲线家族的族谱。「STD」中罗列了多个其他标准,例如Brainpool曲线系列、BN曲线系列、MNT曲线系列等,这些系列的背后都代表了一种独特的曲线生成哲学,或是为了提供可验证的随机数,或是为了提供满足Paring的特性,或是为了提高抗攻击的能力等等,每一份精心选择的参数都是一群数学家们巧夺天工的设计。
后话
古有拆文解字,参透汉字玄机,道破人生天机;
而今咬文嚼字,摸清椭圆原理,揭开曲线家谱。
始于名字,解码secp256k1,厘清标准;
终于名字,问祖weierstrass,致敬大神。
通过了解椭圆曲线之间的内在关系,对其设计有了更多一点的理解。知道的更多了,不知道的也更多了,那些特殊曲线的数学原理是什么?为什么具有更高的计算效率?性能能提升多少?…
又是一个深夜,拥抱最新的收获,夹杂更多的困惑。电脑中正好在播放“把太细的神经割掉,会不会比较睡得着…“
参考资料
SEC1:SEC2:https://www.secg.org/sec1-v2.pdf
SEC2:https://www.secg.org/sec2-v2.pdf
NIST:https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.186-4.pdf
STD:Home | Standard curve database
SafeCurves:https://safecurves.cr.yp.to
Koblitz Curves:https://link.springer.com/content/pdf/10.1007%2F3-540-46766-1_22.pdf
Weierstrass Equation:LMFDB - Weierstrass equation or model (reviewed)
Montgomery Curve wiki:https://en.wikipedia.org/wiki/Montgomery_curve
Twisted Edward Curve wiki:https://en.wikipedia.org/wiki/Twisted_Edwards_curve
Edward Curve wiki:https://en.wikipedia.org/wiki/Twisted_Edwards_curve
ECDSA wiki:https://en.wikipedia.org/wiki/EdDSA#Ed25519
Curve25519 wiki:https://en.wikipedia.org/wiki/Curve25519
Curve25519 paper:http://cr.yp.to/ecdh/curve25519-20060209.pdf
Ed25519 paper:http://ed25519.cr.yp.to/ed25519-20110926.pdf
了解更多干货内容,请关注FISCO BCOS开源社区公众号,访问FISCO BCOS代码仓库可下载项目所有源代码:https://github.com/FISCO-BCOS/FISCO-BCOS,欢迎点击页面右上角star收藏,获取最新版本。
这篇关于一场椭圆曲线的寻根问祖之旅 | FISCO BCOS密码学探究的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






