2022.9.19西瓜书3.3对数几率回归编程

题目： 编程实现对数几率回归，并给出西瓜数据集3.0α上的结果。

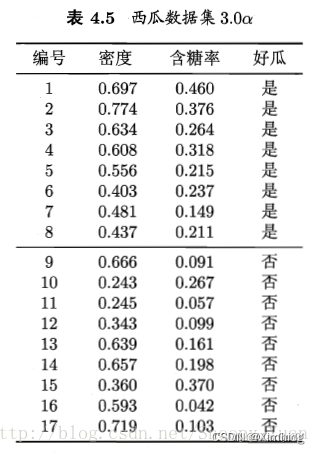
  代码转自：西瓜书——第三章课后习题，本文就代码进行了解读和注释。

import numpy as np
import math
import matplotlib.pyplot as plt#导入数据到变量data_x和data_y
data_x = [[0.697, 0.460], [0.774, 0.376], [0.634, 0.264], [0.608, 0.318], [0.556, 0.215], [0.403, 0.237],[0.481, 0.149], [0.437, 0.211],[0.666, 0.091], [0.243, 0.267], [0.245, 0.057], [0.343, 0.099], [0.639, 0.161], [0.657, 0.198],[0.360, 0.370], [0.593, 0.042], [0.719, 0.103]]
data_y = [1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]#定义combine函数表示beta*x，beta=(w,b),w和b是我们要求的参数，在这道题中我们要求的是一个二元（横轴密度和纵轴含糖率）函数的两个参数
def combine(beta, x):x = np.mat(x + [1.]).T #.T表示转置return beta.T * x#定义sigmoid函数，将beta*x带入到原来的x中
def predict(beta, x):return 1 / (1 + math.exp(-combine(beta, x)))def p1(beta, x):return math.exp(combine(beta, x)) / (1 + math.exp(combine(beta, x)))beta = np.mat([0.] * 3).T#beta是一个三行的0列矩阵#迭代次数为50，此题采用牛顿法
steps = 50 for step in range(steps):    #循环50次param_1 = np.zeros((3, 1))  #创建一个三行一列的0矩阵for i in range(len(data_x)):  #data_x的行数为17，循环17次x = np.mat(data_x[i] + [1.]).T  #选取data_x的第i行加上元素1后进行转置变成3行一列的矩阵param_1 = param_1 - x * (data_y[i] - p1(beta, data_x[i]))  #课本公式3.30param_2 = np.zeros((3, 3))for i in range(len(data_x)):x = np.mat(data_x[i] + [1.]).Tparam_2 = param_2 + x * x.T * p1(beta, data_x[i]) * (1 - p1(beta, data_x[i]))  #课本公式3.31last_beta = betabeta = last_beta - param_2.I * param_1   #课本公式3.29，.I函数可以求矩阵的逆if np.linalg.norm(last_beta.T - beta.T) < 1e-6:  #对括号里的矩阵求二范数print(step)        breakfor i in range(len(data_x)):if data_y[i] == 1:plt.plot(data_x[i][0], data_x[i][1], 'ob')  #参数o表示圆形，b表示蓝色else:plt.plot(data_x[i][0], data_x[i][1], '^g')  #参数^表示上三角形，g表示绿色
w_0 = beta[0, 0]  # 取出参数
w_1 = beta[1, 0]  # 取出参数
b = beta[2, 0]    # 取出参数
print(w_0, w_1, b)
x_0 = -b / w_0 #(x_0, 0)
x_1 = -b / w_1 #(0, x_1)
plt.plot([x_0, 0], [0, x_1])  #绘制(x_0, 0)到(0, x_1)的曲线，斜率为-w_0/w_1
plt.show()

结果如下：

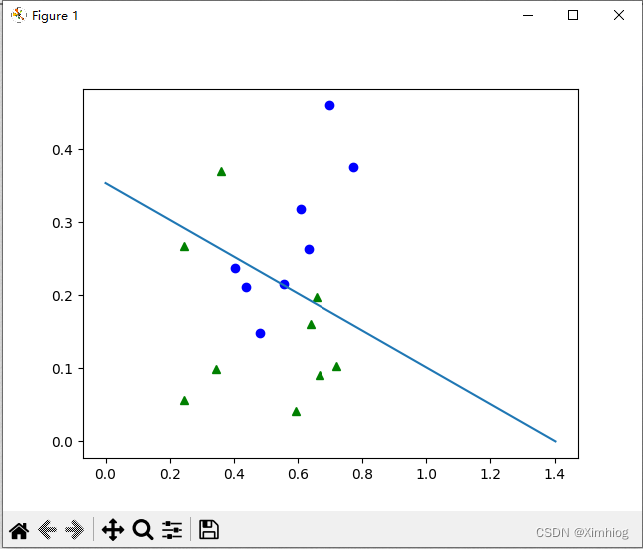
.plot函数参考文章：Python直接使用plot()函数画图