常见混沌序列的生成及分布展示（合集、含代码）

2023-11-22 12:40
文章标签 代码 分布 常见 展示 生成 序列 合集 混沌

本文主要是介绍常见混沌序列的生成及分布展示（合集、含代码），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

分别列举很多种常见的混沌序列，并绘制出其散点图、直方图，这两种图就能直观的观察没种混沌序列的分布了。另外，有些混沌序列参数初始取值范围需要去看对应混沌序列的分岔图，对于只是使用一下混沌序列而不是深究混沌系统的朋友们来说，生成分岔图的步骤就多次一举了，可以直接用我给出的参数。不过分岔图的生成可以考虑后期再补上（20223.6.8日画饼）。在最后会有一个生成整数混沌序列的代码，经过测试效果很不错。

一、混沌序列

百度百科这样介绍混沌序列：混沌序列是一种确定系统中出现的无规则的运动。混沌的离散情况常常表现为混沌序列，混沌序列是由混沌模型生成的具有混沌特性的序列，混沌序列中蕴涵着系统丰富的动力学信息，混沌序列是混沌理论通向现实世界的一个桥梁，是混沌的一个重要应用领域。


做一下个人见解的解释，混沌就是一种无序的状态，而混沌序列就是这种无序状态的数字表现，通常会用一些确定的数学公式去计算得到。


混沌序列可以用来代替随机数生成的，据某篇论文说混沌序列比伪随机数生成器产生的值要好。当然，由于混沌序列的不确定性、无周期性，在密码学方面也有很多的应用，这里我就不太懂了。

本文的混沌序列的公式是在论文和别的网页截的屏（LaTeX用的不太好，公式录入不太熟练），还有一点，可能本文列出的混沌序列的表达式和别的地方不太一样，原因是我参考的论文有些可能是改进变形后的混沌序列，但我会尽量保证使用最经典的或者最常用的来描述。如果有不对的地方，欢迎评论指出。


二、常见混沌序列及其生成


2.1 Logistic 映射


Logistic 映射，又称虫口映射，是最经常用到的一种映射方式：

Z_{k+1}=\mu Z_{k}(1-Z_{k})

其中Z_{0}\notin {0,0.25,0.5,0.75,1.0},\mu \in (3,4]

Matlab代码如下:

% 产生Logistic 混沌序列
x0 = 0.2983;    % 据本人经验，初始值至少取到小数点后三位效果才更好
len = 1000;
squence = zeros(1,len);
xn = x0;
for i=1:lenxn = 4*xn*(1-xn);squence(i) = xn;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
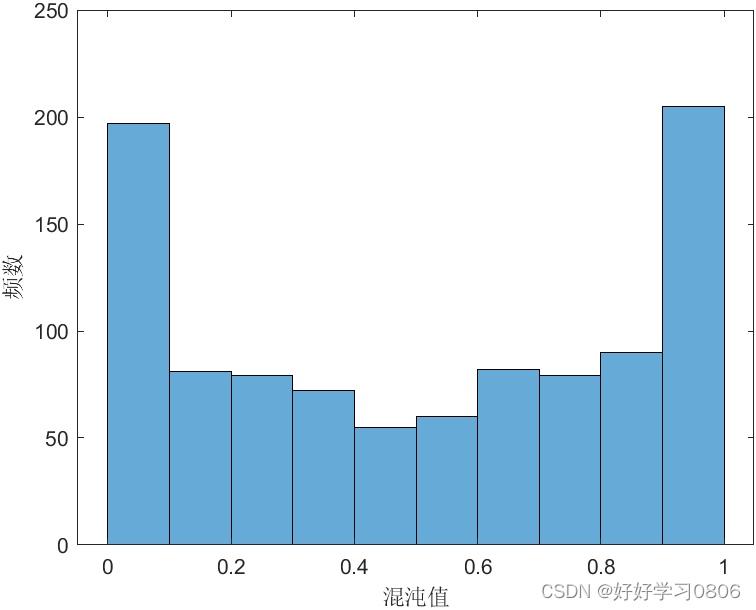
ylabel('频数')

效果图如下：

 

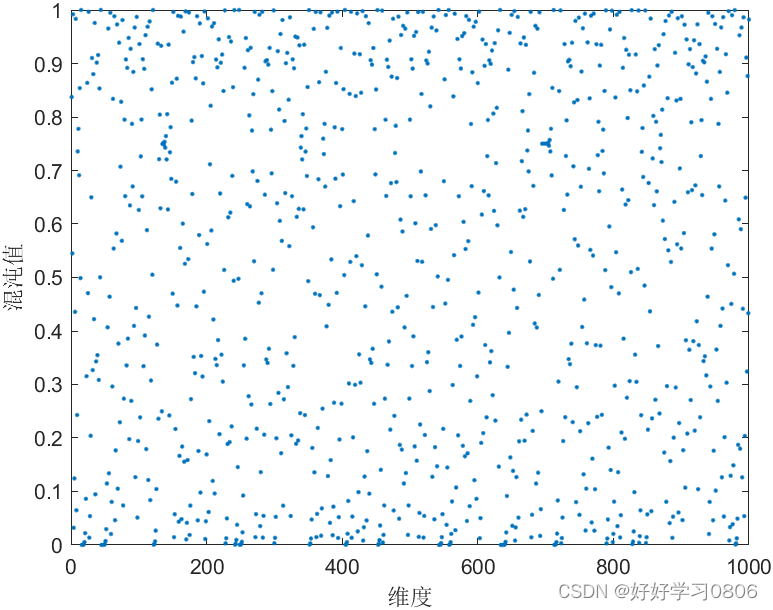
2.2 PWLCM 映射

这个用在图像加密的多些，分布很均匀。表达式如下：

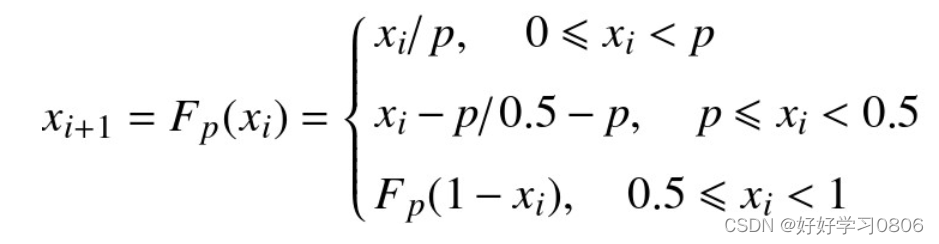
 其中：p是参数取值范围为(0,0.5),xi∈（0,1)。

 Matlab代码如下：

% 产生PWLCM混沌序列
clc;
clear;
close all;
x0=0.347;
p=0.439;
len=1000;
squence=zeros(1,len);
xn=x0;
for i=1:lenif(xn>=0&&xn<p)xn=xn/p;squence(i)=xn;elseif(xn>=p&&xn<0.5)xn=(xn-p)/(0.5-p);squence(i)=xn;elseif(xn>=0.5&&xn<1)xn=(1-xn);% 懒得写递归了，就这样吧if(xn>=0&&xn<p)xn=xn/p;squence(i)=xn;elseif(xn>=p&&xn<0.5)xn=(xn-p)/(0.5-p);squence(i)=xn;endend
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

效果如下：

2.3 Singer 映射

这个我不太了解，长得很奇怪，其表达式如下：

其中：μ的范围为（0.9,1.08）,Z0的范围为（0,1）。

Matlab代码如下：

z0 = rand;    
len = 1000;
squence = zeros(1,len);
zn = z0;
u=1.07;
for i=1:lenzn=u*(7.86*zn-23.31*zn^2+28.75*zn^3-13.302875*zn^4);squence(i)=zn;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

效果如下：

2.4 Sine 映射

表达式如下:

 其中：初始值x0∈(0,1);混沌系统控制参数μ∈[0,4],当μ在区间(3.48,3.72)和(3.8,4)之内时，系统处于混沌状态。

其matlab代码如下：

x0 = rand;    
len = 10000;
xn=x0;
squence = zeros(1,len);
u=3.999;
for i=1:lenxn=(u/4)*sin(pi*xn);squence(i)=xn;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

 效果如下：

 

2.5 Gaussian映射

就是高斯映射，找了好久的原论文，这个很多人可能搜到的都不一样，我不知道为什么国内的很多论文用的和这个完全不一样，但是名字一样。这个数学表达式如下：

 其中：α的取值范围为：[4.7,17],c的取值范围为[-1,1]。

这个总是没有混沌状态，我不会了。

2.6 Tent映射

又称帐篷映射，其数学表达式如下：

 Matlab代码如下：

z0 = rand;
len = 10000;
zn=z0;
p=0.499;
squence = zeros(1,len);
for i=1:lenif zn<pzn=zn/p;elsezn=(1-zn)/(1-p);endsquence(i)=zn;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

 其效果如下：

 2.7 Bernoulli 映射

这个分布也很均匀，数学表达式如下：

Matlab代码如下：

z0 = rand;
len = 10000;
p=0.479;
zn=z0;
squence = zeros(1,len);
for i=1:lenif(zn>0&&zn<=1-p)zn=zn/(1-p);elsezn=(zn-1+p)/p;endsquence(i)=zn;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

效果如下：

2.8 Chebyshev 映射

数学表达式如下：

 w的取值已经列出了，x0的取值范围为[-1,1]。

其Matlab代码如下：

x0=0.299;
w=3;
len = 10000;
p=0.479;
xn=x0;
squence = zeros(1,len);
for i=1:lenxn=cos(w*acos(xn));squence(i)=xn;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

其效果如下：

 

2.9 Circle 映射

其数学表达式如下：

 其matlab代码如下：

z0=rand;
len=10000;
a=0.5;
b=2.2;
zn=z0;
squence = zeros(1,len);
for i=1:lenzn=zn+a-mod((b/(2*pi))*sin(2*pi*zn),1);squence(i)=zn;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

效果如下：

2.10 Cubic 映射

最常用到之一，其数学表达式如下:

 其中，ρ为控制系数，没有具体的范围，但是对结果影响很大。x0的范围为(0,1)。

其matlab代码如下：

x0=rand;
len=10000;
p=2.595;
xn=x0;
squence = zeros(1,len);
for i=1:lenxn=p*xn*(1-xn^2);squence(i)=xn;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

效果如下：

PS：直方图左低右高，不是一样高。

2.11 Sinusoidal 映射

数学表达如下：

 Matlab代码如下：

z0=0.7;
len=10000;
a=2.3;
zn=z0;
squence = zeros(1,len);
for i=1:lenzn=a*zn^2*sin(pi*zn);squence(i)=zn;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

效果如下：

2.12 ICMIC 映射

无限折叠迭代混沌映射，数学表达式如下：

 Matlab代码如下：

z0=rand;
len=10000;
a=100;
zn=z0;
squence = zeros(1,len);
for i=1:lenzn=sin(a/zn);squence(i)=zn;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

效果图如下：

 

三、 使用某一混沌序列生成指定范围的整数混沌序列

这是我碰到的一个问题，自己写了下面这样的代码，按注释更改后，可以直接用。

以Logistic 混沌序列为例，代码如下：

% 获得5~10范围内的整数Logistic混沌序列
x0 = rand;
len = 10000;
squence = zeros(1,len);
xn = x0;
max=10;             % 所选范围的最大整数
min=5;              % 所选范围的最小整数
chunk=1/(max+1-min);  % 分子表示混沌序列的最大值减最小值，一般的混沌序列都在0~1之间，也就是1-0=1。chunk表示分块大小。
for i=1:lenxn = 4*xn*(1-xn);result=floor(xn/chunk)+min;squence(i) = result;
end
% 绘制散点图
figure
plot(squence,'.')
xlabel('维度')
ylabel('混沌值')
% 绘制直方图
figure
histogram(squence)
xlabel('混沌值')
ylabel('频数')

结果如下：

 本篇文章是边写边学习的，前面可能会有些不太正确的地方，如有错误，不吝赐教。

这篇关于常见混沌序列的生成及分布展示（合集、含代码）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/410212。

相关文章

vscode保存代码时自动eslint格式化图文教程

vscode保存代码时自动eslint格式化图文教程

《vscode保存代码时自动eslint格式化图文教程》：本文主要介绍vscode保存代码时自动eslint格式化的相关资料,包括打开设置文件并复制特定内容,文中通过代码介绍的非常详细,需要的朋友... 目录1、点击设置2、选择远程--->点击右上角打开设置3、会弹出settings.json文件，将以下内
阅读更多...
SQL Server使用SELECT INTO实现表备份的代码示例

SQL Server使用SELECT INTO实现表备份的代码示例

《SQLServer使用SELECTINTO实现表备份的代码示例》在数据库管理过程中,有时我们需要对表进行备份,以防数据丢失或修改错误,在SQLServer中,可以使用SELECTINT... 在数据库管理过程中，有时我们需要对表进行备份，以防数据丢失或修改错误。在 SQL Server 中，可以使用 SE
阅读更多...
Python调用另一个py文件并传递参数常见的方法及其应用场景

Python调用另一个py文件并传递参数常见的方法及其应用场景

《Python调用另一个py文件并传递参数常见的方法及其应用场景》：本文主要介绍在Python中调用另一个py文件并传递参数的几种常见方法,包括使用import语句、exec函数、subproce... 目录前言1. 使用import语句1.1 基本用法1.2 导入特定函数1.3 处理文件路径2. 使用ex
阅读更多...
MybatisGenerator文件生成不出对应文件的问题

MybatisGenerator文件生成不出对应文件的问题

《MybatisGenerator文件生成不出对应文件的问题》本文介绍了使用MybatisGenerator生成文件时遇到的问题及解决方法,主要步骤包括检查目标表是否存在、是否能连接到数据库、配置生成... 目录MyBATisGenerator 文件生成不出对应文件先在项目结构里引入“targetProje
阅读更多...
python实现pdf转word和excel的示例代码

python实现pdf转word和excel的示例代码

《python实现pdf转word和excel的示例代码》本文主要介绍了python实现pdf转word和excel的示例代码,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价... 目录一、引言二、python编程1，PDF转Word2，PDF转Excel三、前端页面效果展示总结一
阅读更多...
在MyBatis的XML映射文件中＜trim＞元素所有场景下的完整使用示例代码

在MyBatis的XML映射文件中＜trim＞元素所有场景下的完整使用示例代码

《在MyBatis的XML映射文件中＜trim＞元素所有场景下的完整使用示例代码》在MyBatis的XML映射文件中,trim元素用于动态添加SQL语句的一部分,处理前缀、后缀及多余的逗号或连接符,示... 在MyBATis的XML映射文件中，<trim>元素用于动态地添加SQL语句的一部分，例如SET或W
阅读更多...
Python使用qrcode库实现生成二维码的操作指南

Python使用qrcode库实现生成二维码的操作指南

《Python使用qrcode库实现生成二维码的操作指南》二维码是一种广泛使用的二维条码,因其高效的数据存储能力和易于扫描的特点,广泛应用于支付、身份验证、营销推广等领域,Pythonqrcode库是... 目录一、安装 python qrcode 库二、基本使用方法1. 生成简单二维码2. 生成带 Log
阅读更多...
Spring常见错误之Web嵌套对象校验失效解决办法

Spring常见错误之Web嵌套对象校验失效解决办法

《Spring常见错误之Web嵌套对象校验失效解决办法》：本文主要介绍Spring常见错误之Web嵌套对象校验失效解决的相关资料,通过在Phone对象上添加@Valid注解,问题得以解决,需要的朋... 目录问题复现案例解析问题修正总结  问题复现当开发一个学籍管理系统时，我们会提供了一个 API 接口去
阅读更多...
使用C#代码计算数学表达式实例

使用C#代码计算数学表达式实例

《使用C#代码计算数学表达式实例》这段文字主要讲述了如何使用C#语言来计算数学表达式,该程序通过使用Dictionary保存变量,定义了运算符优先级,并实现了EvaluateExpression方法来... 目录C#代码计算数学表达式该方法很长，因此我将分段描述下面的代码片段显示了下一步以下代码显示该方法如
阅读更多...
python多进程实现数据共享的示例代码

python多进程实现数据共享的示例代码

《python多进程实现数据共享的示例代码》本文介绍了Python中多进程实现数据共享的方法,包括使用multiprocessing模块和manager模块这两种方法,具有一定的参考价值,感兴趣的可以... 目录背景进程、进程创建进程间通信 进程间共享数据共享list实践背景 安卓ui自动化框架，使用的是
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2