白手起家学习数据科学 ——k-Nearest Neighbors之“维度诅咒”(九)

本文主要是介绍白手起家学习数据科学 ——k-Nearest Neighbors之“维度诅咒”(九)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

维度诅咒(The Curse of Dimensionality)

KNN在高维空间运行会出现”维度诅咒”的问题，那是因为在高维空间太广阔，高维空间的数据点不趋向接近另外的数据点。有一个办法可以证明这一点，随机产生很多对d维度的向量，然后计算每对的向量距离。

产生随机数据点：

def random_point(dim):return [random.random() for _ in range(dim)]

生成每对(num_pairs)向量的距离：

def random_distances(dim, num_pairs):return [distance(random_point(dim), random_point(dim))for _ in range(num_pairs)]

我们会计算维度从1到100，每一维度计算出10000个距离，使用这些距离计算每一维的平均距离和找出最小距离：

dimensions = range(1, 101)avg_distances = []
min_distances = []random.seed(0)
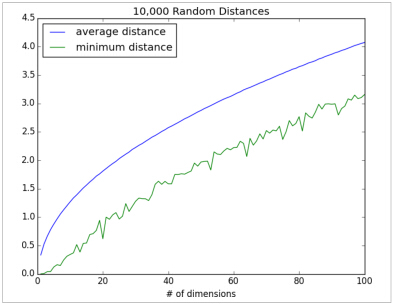
for dim in dimensions:distances = random_distances(dim, 10000) # 10,000 random pairsavg_distances.append(mean(distances)) # track the averagemin_distances.append(min(distances)) # track the minimum

当维度增加时，数据点之间的平均距离也增加，但是更重要的问题是在最近距离与平均距离的比率：

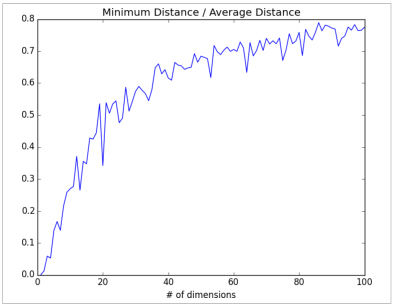
min_avg_ratio = [min_dist / avg_distfor min_dist, avg_dist in zip(min_distances, avg_distances)]

在低维数据集中，最小距离数据点更加接近平均值；在高维数据集中，最小距离数据点不接近平均值，这个意味着最小距离的2个数据点并不是很接近。

解决方案对高维空间进行降维。

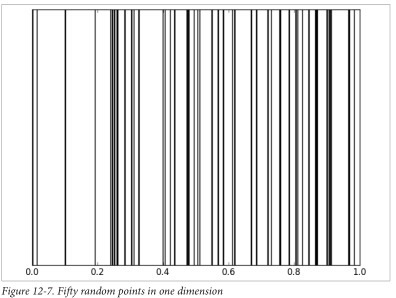
在0到1之间，在一维空间里，你提取50个随机点，你将得到极好的且紧凑的样本：

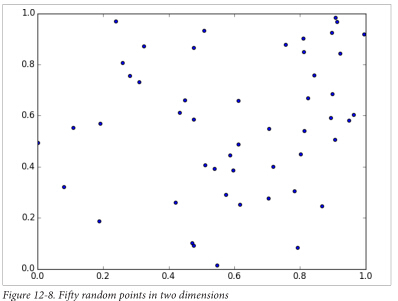
在2维空间里，提取50个随机点，你会发现随机点零散的覆盖在2维空间里：

在3维空间里，你会得到更加零散的随机点：

matplotlib不能画4维空间，这是我们能做的最大限度了，但是这足够发现有很多空的空间，且在随机点周围没有太多的数据点。在更高维空间，除非你得到更加多的数据(指数增加的数据)，否者这些大且空的空间表示没有数据点的区域，你想在你的模型中使用是非常不准确。

所以，如果你正在尝试在高维空间使用最近邻模型，那么一个好的主意是降维。下一章节中我们将要介绍朴素贝叶斯(Naive Bayes)。

这篇关于白手起家学习数据科学 ——k-Nearest Neighbors之“维度诅咒”(九)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---