本文主要是介绍干货分享:游戏场景管理的八叉树算法解析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
转自:https://www.gameres.com/665565.html
八叉树(octree)是三维空间划分的数据结构之一,它用于加速空间查询,例如在游戏中:
1.加速用于可见性判断的视锥裁剪(view frustum culling)。
2.加速射线投射(ray casting) ,如用作视线判断或枪击判定。
3.邻近查询(proximity query),如查询玩家角色某半径范围内的敌方NPC。
4.碰撞检测的粗略阶段(broad phase),找出潜在可能碰撞的物体对。
总括而言,前3个应用都是加速一些形状(frustum、ray、proximity shape如球体)的相交测试(intersection test)。
简单来说,八叉树的空间划分方式是,把一个立方体分割为八个小立法体,然后递归地分割小立方体。

相似地,四叉树把一个正方形空间分割成四个小正方形。由于三维空间较难理解,之后本答案主要以四叉树作图示解释。
四/八叉树有多种变种,先谈一个简化的情况,就是假设所有物体是一个点,这样比较容易理解。
把每点放到正方形空间里,若该正方形含有超过一个点,就把该正方式分割,直至每个小正方形(叶节点)仅含有一个点,就可以得出以下的分割结果:
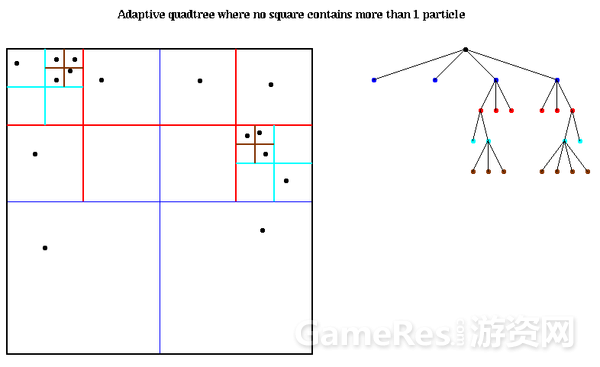
这种做法是adaptive的,就是说按照一定的条件(叶节点只能有一个点)来进行分割。实际上,我们可以设置其他条件去决定是否分割一个叶节点,例如节点内的点超过10个,或是最多分割4层就不再分割等等。
在分割时,我们只需检查点是在每个轴的哪一方,就能知道该点应放置在哪个新的节点里。
建立了一个四/八叉树之后,我们可以得出一个重要特性:
如果一个形状S与节点A的空间(正方形/立方体)不相交,那么S与A子树下的所有点都不相交。
那么,在相交测试中,我们可以从根节点开始,遍历四/八叉树的节点,如节点相交就继续遍历,如不相交就放弃遍历该子树,最后在叶节点进行形状与点的相交测试。这样做,一般能剔除许多点,但注意最坏的情况是所有点集中在一起,那么就不起加速作用。
当创建了一个四/八叉树之后,如问题所提及,有时候需要新增、删除物体(目前我们谈及的是点),以及更新物体(点)的位置。
更新位置的最简单实现,就是删去物体再重新安插。然而,显然的优化方法就是,检查旧位置和新位置是否位于同一个叶节点的正方/立方范围里,如果没超出范围,就不需要做删除再安插的工作。
但如果超出范围呢?除了简单地从根开始找合适的节点,也可以使用一些搜寻方法找到相邻的节点,如[1]。这里就不谈这些细节了。
了解最基本的四/八叉树后,可以把问题扩充至管理占面积/体积的物体。虽然我们可以每次比较场景物体和正方形/立方体是否相交,但为了性能,一般是使用物体的包围体(bounding volume)而不是物体本身。例如是使用包围球(bounding sphere)、轴对齐包围盒(axis-aligned bounding box, AABB)或定向包围体(oriented bounding box, OBB)。这个做法是保守的。
但无论是用物体的精确形状,还是使用包围体积,把它们放置在四/八叉树中会有一个问题:它们可能会与节点的边界相交。例如
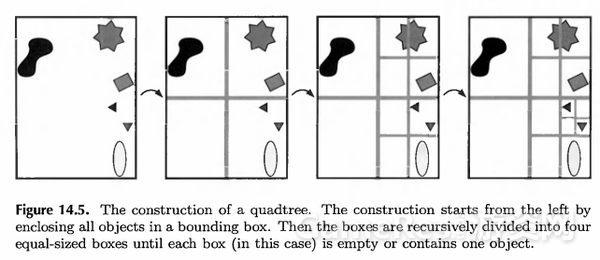
在上图中,七角星最后处于两个叶节点。这时候至少有两个解决方法:
1.所有与物体相交的子节点都引用至该物物体。在此例子中,有两个叶节点都引用七角星物体。
2.令中间节点(非叶节点)也能放置物体。在此例子中,上一层的中间节点(就是右上的正方形)放置七角星物体。
第一种方法的范围比较精确,但如果物体的大小相差很大,大体积的物体便需要被大量小范围的叶节点引用,而且管理上也会很麻烦。第二种做法是较常用的方法。然而,第二种方法的范围可能非常大,例如物体刚好在场景的中心,即使是一个体积很小的物体,都只能放于根节点里。
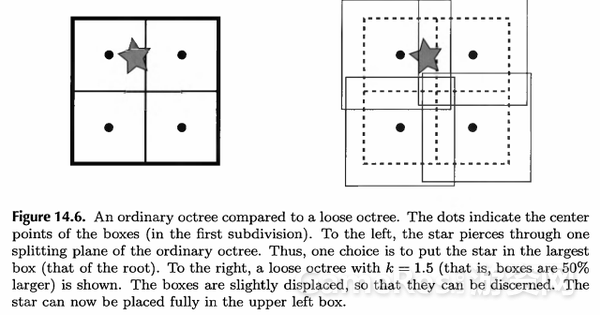
要解决这个问题,可以考虑到在相交测试中,扩大包围盒总是保守的(这里的保守是指近似化不会做成错误结果)。如果把四叉/八叉树的正方/立方空间当作包围盒,那么扩大这些包围盒以容纳刚好在边界上相交的物体也是保守的。这就是松散四/八叉树(loose quadtree/octree)[2] 的思路。
以上所说的都是一些基本原理,在实现时要考虑具体的数据结构、内存布局等问题。现在一般认为,完全使用八叉树可能不利于缓存,用一些扁平的结构并利用SIMD可能更可提高性能,或是需要混合的方案,如八叉树只有两、三层,叶节点内使用扁平的方式储存各种包围体。
因此,除了传统的四/八叉树实现,也可以参考一些更新的技术,例如OpenVDB 中的一些思路。
[1] Frisken, Sarah F., and Ronald N. Perry. "Simple and efficient traversal methods for quadtrees and octrees." Journal of Graphics Tools 7.3 (2002): 1-11.
[2] Ulrich, Thatcher. "Loose octrees." Game Programming Gems 1 (2000): 434-442.
[3] K. Museth, “VDB: High-Resolution Sparse Volumes With Dynamic Topology”. ACM Transactions on Graphics, Volume 32, Issue 3, Pages 27:1-27:22, June 2013. http://www.museth.org/Ken/Publications_files/Museth_TOG13.pdf <//link.zhihu.com/?target=http://www.museth.org/Ken/Publications_files/Museth_TOG13.pdf>
相关阅读:[翻译]四叉树和八叉树的剔出选择
这篇关于干货分享:游戏场景管理的八叉树算法解析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





