matlab + 3轴机器人、3轴机械臂求逆解、使用xyz求逆解

关于3轴仅使用xyz位置坐标求逆解，我查阅的关于3轴求逆解的文章比较简略，没有具体代码实现过程，以及算法，我根据别人文章的思路，结合自己机械臂的需求，整理了一下求解过程以及代码实现过程。图示为常见的 3轴机械臂

3轴机械臂求逆解的方法

1.几何法（使用的方法）

2.解析法（提供解法）

提示：以下是本篇文章正文内容，下面案例可供参考

一、几何法

1.建立3轴映射模型

下图为我所使用的3机械臂模型，由底座、大臂、小臂组成。

关于机械臂的DH建模方法不在赘述，对其建立运动学模型也不再赘述大致如下图：

最关键的点在于对机械臂模型进行抽象化，映射到几何坐标系中：

一，假设条件
坐标系采用右手坐标系，如上图所示
机械臂的底座位于右手坐标系的XY平面
底座旋转轴的位置，即为坐标系的原点位置，即上图做所视的O点
我们把AB线所表示臂称之为大臂，BC线所表示的臂称之为小臂
OA线与XY平面的夹角为θ(我的机械臂模型这里是0°，没有仰角)
AB线与Z轴的夹角为β
AB线与BC线之间的夹角为γ，即大臂与小臂的夹角
点O,A,B,C始终处于同一平面，且此平面与XZ平面之间的夹角为α
机械臂的初始位置为A，B，C三点的Y轴坐标为O，B，C点收回到距离Z轴最近的位置
初始位置α=0,β=β0,γ=γ0
已知条件：OA，AB，BC长度，θ角度是0

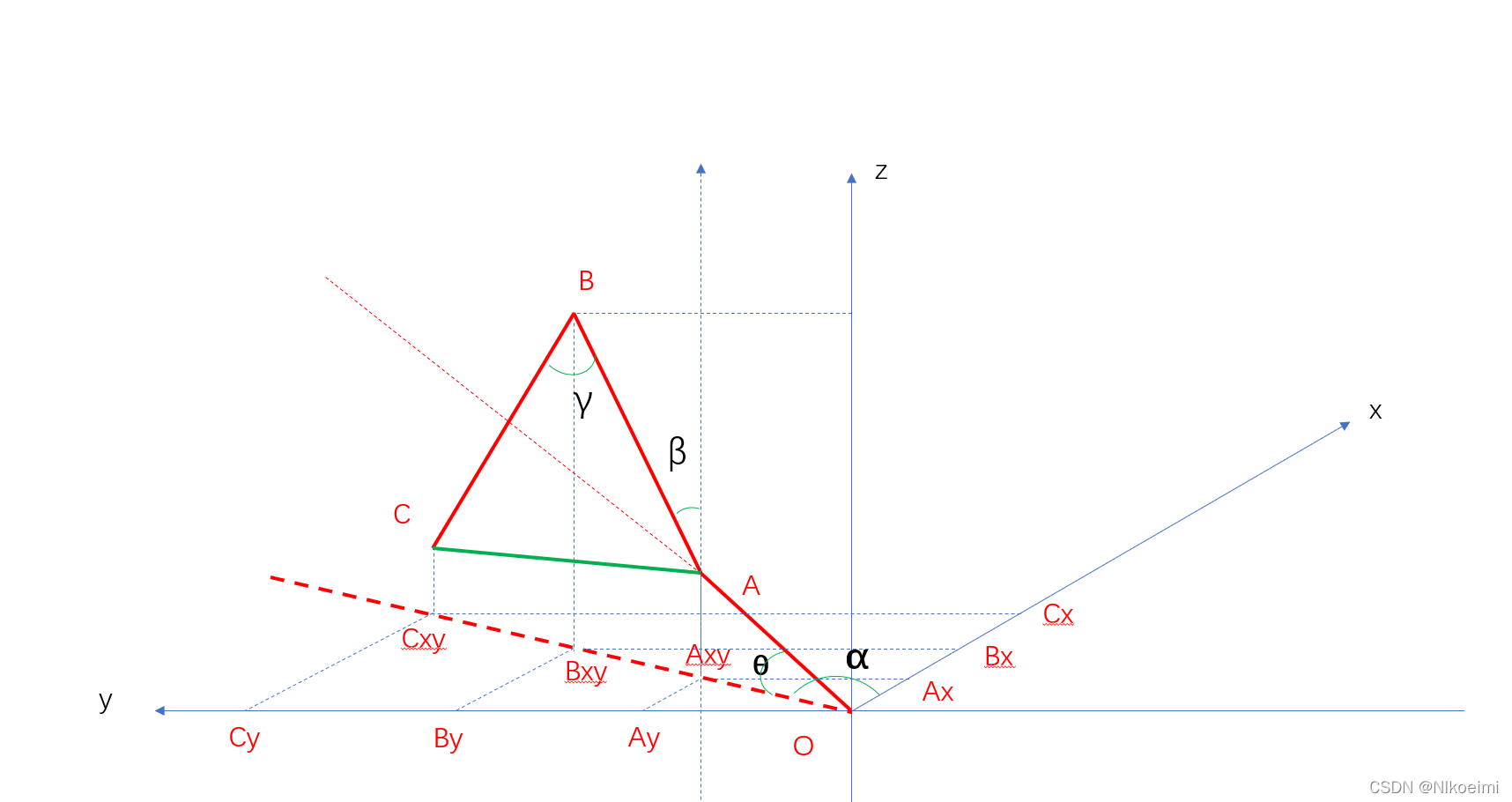
已知 C点的Cx， Cy， Cz3个已知量，求解3个未知量关节角度α,β,γ

2.数学求解

已知C点的坐标(x,y,z)，基于以上假设条件，求解α,β,γ。根据上图几何关系，可以得到以下方程：

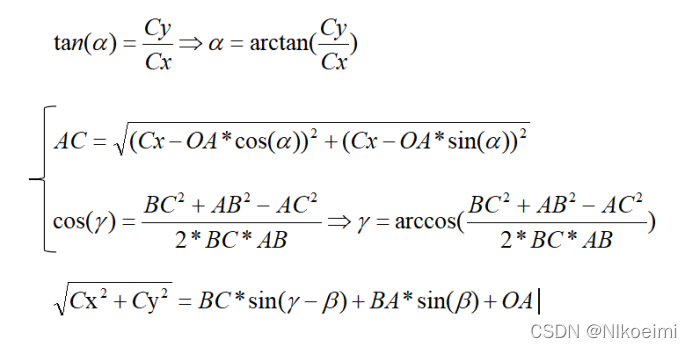
根据上述方程式，即可解出α,β,γ的值。

3.matlab实现

    a1 = 170; %杆1长a2 = 650; %杆2长a3 = 605.4; %杆3长theta1_alpha= atan2(cy,cx);							% 求theta1ac=power(cx-a1*cos(theta1_alpha),2)+power(cy-a1*sin(theta1_alpha),2) +power(cz-cz,2);% 因为杆1是平行xy平面，所以不涉及czcosr=(a3*a3+a2*a2-ac)/(2*a3*a2);theta3_gama= acos(cosr);							% 求theta3eq = @(xx)a1+a3*sin(theta3_gama)*sqrt(1-xx^2)+(a2-a3*cos(theta3_gama))*xx-sqrt(cx*cx+cy*cy);xx0 = sind(0);options = optimoptions(@fsolve, 'OptimalityTolerance',1e-10);[xx] = fsolve(eq, xx0,options);theta2_beta=asin(xx);								% 求theta2fprintf('theta2_beta=%f\n',theta2_beta)% 弧度制fprintf('beta=%f\n',theta2_beta*(pi/180))%角度制

4.求解β的过程

（1）函数solve

S=solve(eqns,vars,Name,Value)

eqns是需要求解的方程组；
vars是需要求解的变量；
Name-Value对用于指定求解的属性（一般用不到）；
S是结果，对应于vars中变量；

（2）函数fsolve

[x,fval,exitflag]=fsolve(fun,x0,options)

其中fun是方程，x0是初值，需要提前设定，options是一些设定要求，可以用optimset函数来实现；exitflag用以描述出口条件。

（3）关于使用matlab求解方程的一些问题

像这总求三角函数的问题，可以考虑化简方程、把三角函数看作一个整体变量、尽量使用数值解代替符号解（解析解）。

二、解析法

1.建立模型找到数学关系

建立直角坐标系后，机械臂末端的位置，也就是坐标系3原点的位置可表示为：

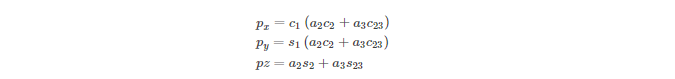
已知 px、py、pz 3个已知量，求解3个未知量关节角度 ϑ1 、ϑ2、 ϑ3。 从代数的角度来看，由于限定关节角度的范围为[−π,π]，故会有多解，从几何角度来看，存在多解情形。

2.求解方法

求解的过程是从关节3 →关节2 →关节1。 首先求解关节3的解：

在列出关节2的解的时候要注意，因为从直观上看c2和s2的组合一共有8种（4个c2，2个s2），由于需要满足三角平方公式，所以只有4种是合法的。

总结

本文旨在使用几何法求逆解并且提供了具体的matlab解beta的方法，关于解析法的过程没有进行代码实现，仅仅是作为理论知识，借助其理解多个解的情形。

参考链接：
1 2 3