Large Scale Metric Learning from Equivalence Constraints (KISSME)

一：介绍

现有的Mahalanobis度量学习方法很多是通过梯度下降来迭代更新M矩阵，监督程度较高（如需要所有样本标签的LMNN方法）和计算复杂（需要大量的迭代）对于样本数目日益增长的大规模数据集是很不友好的。作者从概率的观点，计算发生概率的最大似然比率来计算样本的马氏距离，无需进行昂贵的迭代运算，而且仅需要样本间yij=0或1 （即equivalence constraints）的监督信息，对于大规模数据集非常合适。作者在人脸识别、行人重识别、目标检测等任务的通用的benchmarks上进行了实验，证实了作者所提出方法的优良性能。

二：作者的方法 

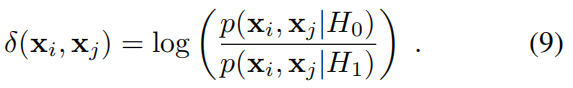
如上图所示，H0表示xi,xj 不是同类，H1表示xi,xj 是同类。delta(xi,xj)就是xi,xj 不是同类的概率除以xi,xj 是同类的概率。显然，当delta(xi,xj)为一个较大的值时，说明H0为真，即xi,xj 不是同类。反之H1为真，即xi,xj 是同类。所以我们可以通过delta(xi,xj)这个函数来测量(xi,xj)样本特征间的距离。

如上图所示，为了不依赖于样本特征向量的分布空间，用两个样本特征间的差值xij = xi - xj来作为delta函数的变量。下面通过最大似然估计的方法，使得训练样本发生的概率最大，来求解p(xij|H0)和p(xij|H1)的参数theata0和theata1。

假设xi和xj同类和不同类时f(xij | theata0)和f(xij | theata0)均是高斯分布（这里的数学知识我不太明白，应该是研究生课程），根据最大似然估计原理，可得解如下：

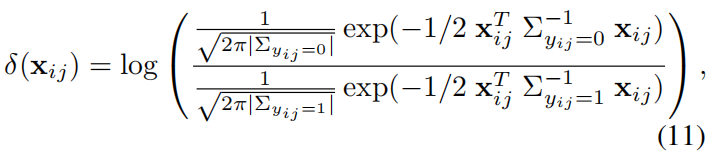
其中： 

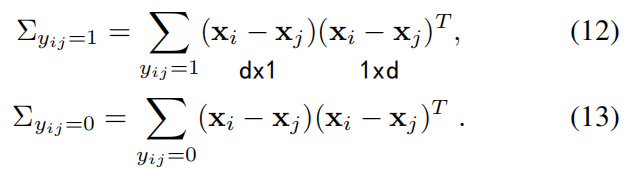
作者指出，高斯的最大似然估计结果等效于以最小二乘方式最小化与平均值的马氏距离。

求log后：

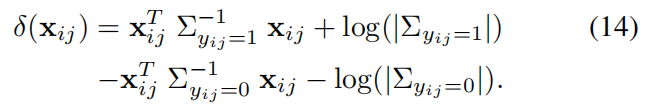
去除常数项后：

所以，整理后KISSME的最终形式为： 

其中 

因为xij为实对称矩阵，所以M^也是个实对称矩阵。通过特征值分析，将M^重新投影为半正定矩阵M（保证距离大于等于0）。 

三： 实验结果

在 LFW数据集上的实验结果如下两张图：

算法时间复杂度分析： 

可以看到，KISSME相比其他方法在时间复杂度上的优势能达到2个数量级以上。 

在人脸验证数据集PubFig上的实验结果：

在行人重识别数据集VIPeR上的实验结果： 

在目标检测数据集 LEAR ToyCars数据集上的结果：

四、结论

In this work we presented our KISS method to learn a distance metric from equivalence constraints. Based on a statistical inference perspective we provide a solution that is very efficient to obtain and effective in terms of generalization performance. To show the merit of our method we conducted several experiments on various challenging large-scale benchmarks, including LFW and PubFig. On all benchmarks we are able to match or slightly outperform state-of-the-art metric learning approaches, while being orders of magnitudes faster in training. On two datasets(VIPeR, ToyCars) we even outperform approaches especially tailored to these tasks.