题目传送:http://codeforces.com/problemset/problem/1009/E
题目大意
给你一个长度为n的序列a,a[i]代表连续走第 i km时,第 i km的花费。现有一段长度为n km的路,输出从头走到尾的花费的期望*2n-1(一定是个整数)对998244353取模后的结果。
输入格式
第一行一个整数 n ,意义如题目大意所述。
第二行 n 个整数,代表 a1, a2, …, an 。
输出格式
一个整数,为花费的期望*2n-1,答案对998244353取模。
数据范围
1 <= n <= 106,1 <= ai <= 106。
解法
首先答案的期望为![]() ,乘上2n-1其实就是每种情况的花费之和。
,乘上2n-1其实就是每种情况的花费之和。
我们考虑每一位对答案的贡献。
考虑第 i 位为连续的第 j 段,那么它的贡献就是![]() 。第 i 位只能是当前连续的第1~i,但当它为第 i 段时,只有2n-i种情况,所以第 i 位贡献为:
。第 i 位只能是当前连续的第1~i,但当它为第 i 段时,只有2n-i种情况,所以第 i 位贡献为:
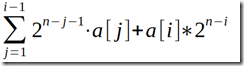
枚举每一位,总共的贡献就是:
貌似时间会炸,但如果我们把它变个型:

从上面那张图到这张图的第一行这一步变化可以用加的次数分析。
然后我们只需枚举一层1~n-1就可以求出答案了,当然,中途一定要记得随时取模,否则爆long long(前两次提交的悲惨经历)。
提交记录和代码:


1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #define P 998244353 5 using namespace std; 6 7 typedef long long LL; 8 LL n, a[1000005], ans, p = 1; 9 10 int main() 11 { 12 scanf("%I64d", &n); 13 for(int i = 1; i <= n; i++) 14 scanf("%I64d", a + i); 15 for(int i = n - 1; i > 0; p = (p << 1) % P, i--) 16 ans = (ans + (n + 2 - i) * p % P * a[i] % P) % P;//随时mod P以免爆炸 17 printf("%I64d\n", (ans + a[n]) % P); 18 19 return 0; 20 }//Rhein_E
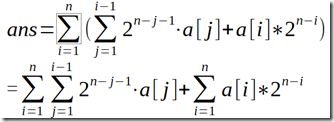

![洛谷 P10584 [蓝桥杯 2024 国 A] 数学题(整除分块+杜教筛)](https://img-blog.csdnimg.cn/direct/674b6510d76b452aac61ec4526244379.png)