m基于GA遗传算法的PMSM永磁同步电机参数最优计算matlab仿真

本文主要是介绍m基于GA遗传算法的PMSM永磁同步电机参数最优计算matlab仿真，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.算法描述

2.仿真效果预览

3.MATLAB核心程序

4.完整MATLAB

1.算法描述

永磁同步电机（PMSM）基本结构为定子、转子和端盖。其中转子磁路结构是永磁同步电机与其它电机最主要的区别，其在很大程度上决定了永磁同步电机的实际性能指标。通常情况下，永磁同步电机的转子磁路结构分为：凸装式、嵌入式和内置式三种结构。目前为止，由于永磁同步电机优越的性能，其越来越受到国内外专家学者的重视，并广泛应用到了工业领域的各个方面。

遗传算法的优化目标可以用如下公式表示：

表示yai控制输出结果；变量ybi表示标准电机的控制输出结果。

基于遗传算法的优化设计方案是目前应用较为广泛的一种优化方法，其在各个工程应用领域具有较多的使用。特别是对于较为复杂的系统，其性能往往是收到诸多因素影响的，而为了达到系统的最佳性能，则需要搜索最佳的参数组合，使得系统具备高性能，低功耗，低成本等优势。而传统的多个参数的最优组合计算往往计算过程较为复杂，而且得到的参数组合也不一定是真实的最优参数，存在较多的问题，而采用遗传优化算法则可以得到提高搜索最优参数组合的效率，并使得参数组合尽可能的接近真实的最优解。

在工程上，通过将电机的设计转换为最优问题，通过数学规划的方法，并借助计算机编程实现算法的高效稳定的运算。GA遗传算法是目前应用最为广泛的全局优化算法，其可以有效解决局部优化问题，并且适用于多目标的优化问题。

遗传算法（Genetic Algorithm）是一类借鉴生物界的进化规律演化而来的随机化搜索方法[17]。它是由美国的J.Holland教授1975年首先提出，其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。遗传算法的这些性质，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域，它是现代有关智能计算中的关键技术。因此，遗传算法本质上是一种搜索最优解的优化技术，其根据适应度函数进行优化，通过种群个体一代又一代的逼近来实现优化功能。

目前，遗传算法主要有如下几个方面的应用：

第一、目标函数的优化处理。目标函数的优化处理是遗传算法最为主要的应用之一，适用于单目标优化问题，多目标优化问题，线性目标优化问题以及非线性目标处理问题等多个领域。

第二、生产调度的优化处理。通过遗传算法可以实现较为复杂的同步电机优化设计问题。

第三、组合优化处理。由于优化问题的日益复杂化，组合优化的优化处理方式得到越来越多的应用，在控制领域，图像处理以及机器学习方面都有着广泛的应用。而遗传算法在求解组合优化问题方面有着较强的计算能力。

基于遗传算法的电机优化设计流程图如下所示：

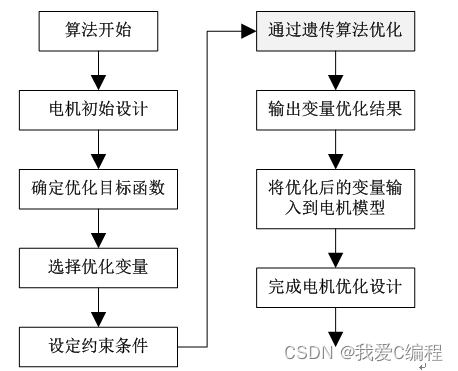
2.仿真效果预览

matlab2022a仿真如下：

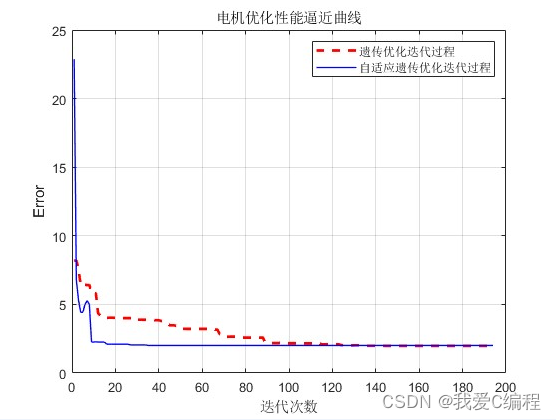
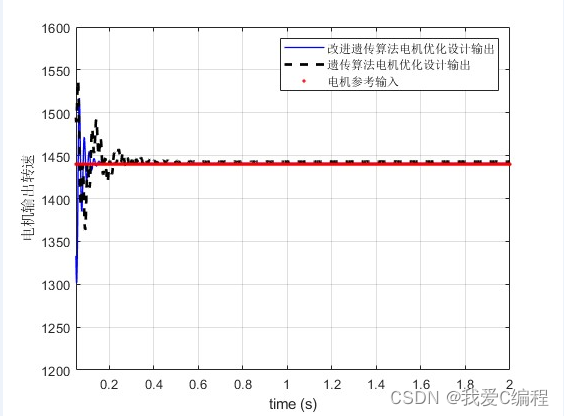
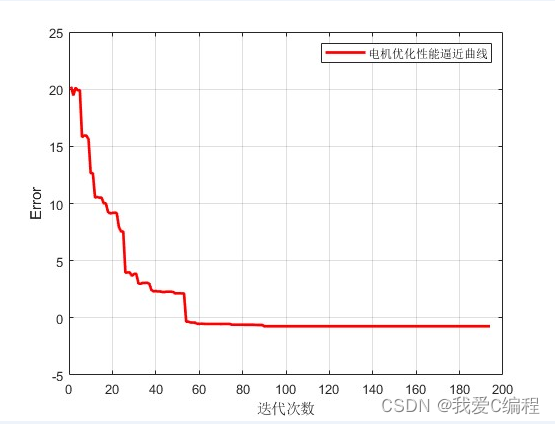
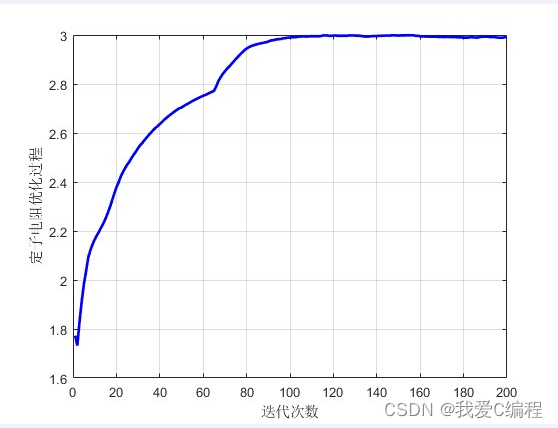
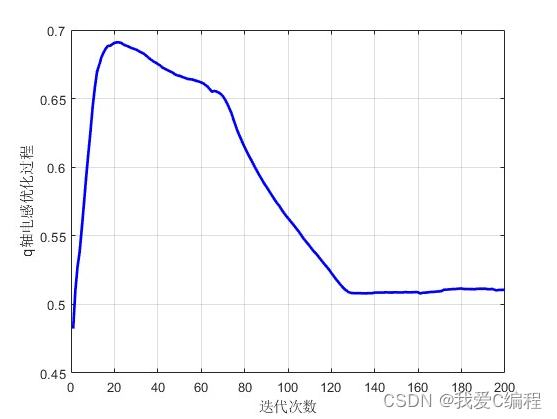
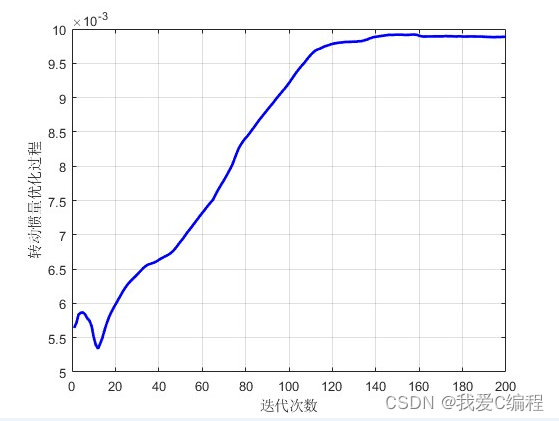
3.MATLAB核心程序

%定义初始值
Rs     = 0.712; %转子电阻
Rr     = 3.789; %定子电阻
M      = 0.295; %磁链
Ld     = 0.311; %d轴电感
Lq     = 0.311; %q轴电感
p      = 2.0;   %极对数
J      = 0.003; %转动惯量
%%
%下面开始使用遗传优化算法
%根据遗传算法进行参数的拟合
MAXGEN = 200;
NIND   = 20;
Nums   = 7;Chrom  = crtbp(NIND,Nums*10);
Sm     = 0.001;
Areas  = [Sm,Sm,Sm,Sm,Sm,1,Sm;1,4,1,1,1,4,0.01];FieldD = [rep([10],[1,Nums]);Areas;rep([0;0;0;0],[1,Nums])];Data1  = zeros(NIND,Nums);
Data2  = zeros(MAXGEN,Nums); gen   = 0;
% randperm(A*B*C)
for a=1:1:NIND %计算对应的目标值epls       = func_obj(Rs,Rr,M,Ld,Lq,p,J);E          = epls;Js(a,1)    = E;
endObjv  = (Js+eps);
gen   = 0; %%
Rs3     = []; %转子电阻
Rr3     = []; %定子电阻
M3      = []; %磁链
Ld3     = []; %d轴电感
Lq3     = []; %q轴电感
p3      = [];   %极对数
J3      = []; %转动惯量Rs4     = []; %转子电阻
Rr4     = []; %定子电阻
M4      = []; %磁链
Ld4     = []; %d轴电感
Lq4     = []; %q轴电感
p4      = [];   %极对数
J4      = []; %转动惯量
while gen < MAXGEN;   genPe0 = 0.995;pe1 = 0.005; FitnV=ranking(Objv);    Selch=select('sus',Chrom,FitnV);    Selch=recombin('xovsp', Selch,Pe0);   Selch=mut( Selch,pe1);   phen1=bs2rv(Selch,FieldD);   size(Objv)size(Chrom)size(FitnV)Rs = [];Rr = [];   M  = [];      Ld = [];Lq = [];   p  = [];     J  = []; for a=1:1:NIND  Rs(a) = phen1(a,1);Rr(a) = phen1(a,2); M(a)  = phen1(a,3); Ld(a) = phen1(a,4); Lq(a) = phen1(a,5); p(a)  = floor(phen1(a,6))+1; J(a)  = phen1(a,7); %计算对应的目标值epls    = func_obj(Rs(a),Rr(a),M(a),Ld(a),Lq(a),p(a),J(a));E       = epls;JJ(a,1) = E;end Objvsel=(JJ);    [Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);   gen=gen+1; %保存参数收敛过程和误差收敛过程以及函数值拟合结论index1     = isnan(JJ);index2     = find(index1 == 1);JJ(index2) = [];Error2(gen) = min(JJ);[VV,II]=min(JJ);Rs3(gen)     = [mean(Rs)]; %转子电阻
Rr3(gen)     = [mean(Rr)]; %定子电阻
M3(gen)      = [mean(M)]; %磁链
Ld3(gen)     = [mean(Ld)]; %d轴电感
Lq3(gen)     = [mean(Lq)]; %q轴电感
p3(gen)      = [mean(p)];   %极对数
J3(gen)      = [mean(J)]; %转动惯量if gen<=64Rs4     = [Rs4,mean(Rs3(1:gen))]; %转子电阻Rr4     = [Rr4,mean(Rr3(1:gen))]; %定子电阻M4      = [M4,mean(M3(1:gen))]; %磁链Ld4     = [Ld4,mean(Ld3(1:gen))]; %d轴电感Lq4     = [Lq4,mean(Lq3(1:gen))]; %q轴电感p4      = [p4,mean(p3(1:gen))];   %极对数J4      = [J4,mean(J3(1:gen))]; %转动惯量
elseRs4     = [Rs4,mean(Rs3(gen-64:gen))]; %转子电阻Rr4     = [Rr4,mean(Rr3(gen-64:gen))]; %定子电阻M4      = [M4,mean(M3(gen-64:gen))]; %磁链Ld4     = [Ld4,mean(Ld3(gen-64:gen))]; %d轴电感Lq4     = [Lq4,mean(Lq3(gen-64:gen))]; %q轴电感p4      = [p4,mean(p3(gen-64:gen))];   %极对数J4      = [J4,mean(J3(gen-64:gen))]; %转动惯量
endend 
[V,I] = min(JJ);
V
Rs_best = Rs(I) 
Rr_best = Rr(I)    
M_best  = M(I)  
Ld_best = Ld(I) 
Lq_best = Lq(I)  
p_best  = p(I) 
J_best  = J(I)
save result.mat Rs_best Rr_best M_best Ld_best Lq_best p_best J_best
02_042m