本文主要是介绍A Survey of Game Theory as Applied to Social Networks,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
摘要
社交网络服务不仅可以帮助人们建立关系,结交新朋友和新伙伴,还可以帮助处理个人信息,分享知识,管理社会关系。社交网络实现了有价值的沟通和协作,带来了额外的商业机会,具有巨大的社会价值。利用假设、定义、分析、建模和优化策略对社会网络问题进行研究是有效的。本文调查了博弈理论在社会网络应用中存在的问题,并将其应用场景分为四类:信息扩散、行为分析、社区检测和信息安全。读者可以清晰地掌握每一个类别的知识应用。最后,在近几年研究的基础上,讨论了博弈论的局限性,并提出了未来社会网络研究的方向。
引言
传统的社交网络方法的缺点是缺乏动态互动。为此,建议使用博弈论来分析不同的场景。通过算法、模型和经验方法分析参与者、行动、策略、收益、均衡和结果。这些因素描绘了博弈模型,并提出了每个参与者的利润函数。结合博弈模型和实际人类行为,总结了优化策略。论文的组织方式如下。第2节通过对研究成果的收集,对博弈论、社会网络等不同方面的应用方法进行了评价,如信息扩散、社区检测、行为分析、信息安全等。第三部分针对目前的局限性提出了未来的研究方向。第四部分对全文进行总结。本文旨在帮助学者们快速认识博弈论在社交网络中的应用;研究人员可以参考本文的一些建议进行进一步的研究。
博弈理论在社交网络中的应用分类
在社会网络研究中,博弈论的应用大多是关于个体的行为和这些个体之间的策略互动。之前的大多数研究人员首先分析了这个问题,然后创建了一个博弈论模型。博弈论模型将每个节点描述为一个自私的节点,它可以选择增加自身收益的动机,状态为博弈策略。该模型恰当地捕捉了个体的自然策略,并描述了社会网络的状态。不同的方向存在着进一步的探索,我们可以得到优秀的模型和方法通过收集、整理、分析、归纳等方法,回顾不同研究中社会网络的各个方面。在文献综述的基础上,我们提出了一个分类研究领域的分类方法,如图1所示,为学者提供了一个社会网络问题的全局视图。

信息扩散应用
在社会网络分析中,大多数用户被定义为节点。个体之间的关系可以用相应节点之间的边抽象地表示,其中的数据沿边分布。关于信息扩散和影响,我们可以分析个人、群体和群体之间的关系。我们在用户关系、网络拓扑、用户心理、知识、反馈传递等多种因素的影响下进行信息扩散。在博弈论的应用中,博弈双方的人可以看作是彼此的个体,也可以看作是邻居的个体,来分析社会网络中的信息扩散。从理性因素和非理性因素两个方面分析了它们在信息传递时的状态、信息传播成本和收益以及优化策略。
最近的一些研究强调了信息扩散的问题[5,11]。Reiffers-Masson等人[5]提出了一个利用非合作博弈的源间竞争模型。Huang et al.[6]采用实证方法从Twitter上收集信息。他们做了一个图解来模拟系统易于分析。信息扩散图如图2所示。

- 5个节点代表5个用户
- 节点之间的边代表他们之间可以共享的新消息。将阈值设为5,参与人1、2、3、4和5的估值分别为7、6、4、2和1。
- 参与人1是第一个消息发起者,传播者只能是2和3。我们可以在图2a中看到这种情况。然后提出了一种策略,通过添加评论和相关信息来增加其他玩家的估值,并丰富原始信息。因此,参与人3加入了扩散过程,如图2b所示。通过这个基本模型,抽象了博弈过程,分析了博弈者的策略和利益。文中还提出了求解纳什均衡解的算法,并给出了数值算例。
所有玩家的策略都是派生出来的。 - 在表1的解中,vi表示参与者对原始信息的估值,si表示参与者的策略文件,并且ui为玩家效用函数,基于边缘上升成本;随着不断增长的努力存在,玩家将其视为收入。表1通过给出系统的参数来证明系统的稳定性,给出了某些参与者采取纳什均衡策略的实例。
- 最后,高估值用户愿意强烈努力丰富原始信息。以上分析采用了实证方法和图形游戏,但没有考虑用户的决策、动机、认知、态度、情感和社会经济联系,这些通常被网络中现有作品所忽略。Jiang et al.[11]考虑了基于网络建模、经验逼近、数据挖掘和用户行为的扩散系统分析。提出了一个应用于社会网络动态信息扩散过程的演化博弈论框架。

社区检测应用
社交网络的另一个常见的网络属性是社区结构特征。也就是说,节点之间的内部连接使社区更紧密,而社区之间的连接则相对稀疏。社区是一群具有共同特征的人;例如,组织,有相同爱好的人的小组,以及公司的部门。社区检测算法可以有效地检测人们的活动和互动对动态社会网络的影响。通过分析社会网络的动态博弈理论,我们可以自然地在社会网络中找到社区,了解其结构,找到优化社区模型,分析社区之间的关系,为网络提供有价值的信息,防止病毒传播等潜在的安全问题。
社区检测是社交网络中的一个热门问题[12-16]。Jiang和Xu[17]引用了一个关于不同群落度分布的图[18]。**根据分析,收益、损失和效用函数是基于智能和自私的行为,比如加入或离开社区。**在图3中,由a表示的三个相关群落;B; andC是定义。节点是感兴趣的节点,分析了其增益和损失函数。
一个智能和自私的代理可以选择一系列的行动-加入或离开社区-以最大化其效用。动态网络被认为是一系列快照。每个快照都有它的社区。通过分析,提出了相应的算法。虽然通过其动态的社区检测博弈可以随着时间的推移平滑地检测社区结构,但只讨论了带有纯策略的博弈,并将每个社区限制为不重叠。调查重叠的案件具有挑战性。Chen等人[19]基于博弈论提出了一种新的有效的签名网络社区划分方法。[20]等人引入了一种博弈论方法来识别社交网络中的互动群体。大多数分析都基于算法和模型。因此,现实的行为和预期的行为之间仍然存在巨大的差距。

行为分析应用
社交网络中的用户行为是一种动态互动,在整个发展过程中不断演变。用户的交互行为反映了社交网络的主要特征。在过去的几年里,许多学者在这一研究领域做出了巨大的贡献。
(1)识别节点属性,挖掘社交网络秘密节点,确定病毒营销中有影响力的个体,挖掘节点中心性。在复杂的社会网络中,探索秘密节点是非常重要的;这样做可以帮助及时发现恐怖分子,向可能的客户推荐某些产品,并找到谣言的来源。有了这些因素,我们就可以轻松有效地控制社交网络的状况。Yang et al.[21]发现了社交网络中的隐蔽节点。根据影响传播基础模型,确定了用户影响策略、常态影响策略、转化策略。随后,他们得到了回报矩阵,如表2所示。
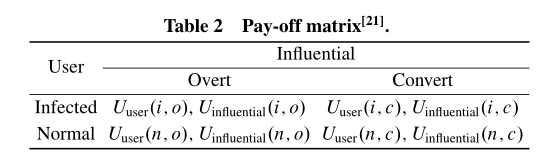
在他们的模型中,用户被分为正常节点和受感染节点。有影响的节点有两种状态:显性或显性。根据贝叶斯定理,在真实数据集和仿真数据集上获取相关参数并计算节点收益的他们使用的方法得到了验证。通过确定网络中的关键部件,可以提高通过这些网络提供的服务的质量。Aadithya和Ravindran[22]提出了计算加权和非加权网络上各种与中心相关的合作博弈Shapley节点值的解析公式。这些公式提供了计算节点中心性的有效且无误差的方法。然而,他们惊人的简单的封闭形式表达式也提供了关于为什么某些节点对网络是相对重要的直觉。在Ref.[23]的模型中,影响博弈可以捕捉玩家的互动和行为,算法可以识别社交网络中的大多数影响节点。
(2)社交网络的两个特征是无标度和小世界,这两个特征是以小世界网络的形成为基础的。Yang和Chen[24]提出了一个博弈论模型和网络形成作为一种博弈,人们在其中寻找长距离和高互惠关。重要的是,他们为社交网络中距离、互惠和可导航性之间的联系提供了重要的新见解。该拓扑模型可以自然地表达在现实环境中的许多游戏的内部结构中。玩家根据周围人的影响做出决定。Rajtmajer等人[25]首次尝试研究进化博弈模型来解释网络暴力的传播。他们通过两种策略制定了一个游戏,每个玩家的行为被分为正常(合作)和虐待(缺陷)。通过对从网上收集的真实数据集的实证测量,他们提供了一个可视化的网络图和相应的度分布,遵循代表的幂律模型。
图4包含了超过787线程的62 060个帖子,得到了一个由2586个独立节点(用户)组成的网络。这些节点由62 931条未加权、无向边连接。图5反映了节点度的分布情况。
在本研究中,提出了一个所有用户之间的单一收益矩阵。进一步的研究可能涉及多个支付矩阵,它可以指示用户的异常并分析不同的支付方案。Kearns等人[26]提出了一个由n个参与人组成的多参与人博弈,每个参与人都有一组有限的纯策略或行动,以及每个参与人的具体收益。随后,他们建立了一个马尔可夫网络,它表示图形博弈的所有相关均衡,描绘了收益等价,并提供了计算相关均衡的一般算法。
社交网络安全应用
社交网络拥有庞大的用户群和大量的信息,这引起了许多入侵者的注意。社交网络的安全性不容忽视。常见的安全问题包括用户隐私信息泄露、财产损失、流氓软件攻击和打开不安全链接。博弈论在社交网络中的应用包括建立用户信任机制,模拟网络控制管理者的活动,控制访问,分析隐私,提出合理的隐私管理策略。博弈论问题应用于网络安全;大多数普通社交网络用户和网络攻击者都可能是游戏的双方。V分析了各种盈利策略,并在仿真系统中测试了结果[7,8,27,28]。社会网络领域的信息安全研究非常丰富。
(1)访问控制
访问控制可以有效保障网络安全。许多学者通过博弈模型实现了对社交网络访问控制的研究。Squicciarini等人[29]采用了两用户游戏模型来解决注册社交网络中的用户认证问题。他们是第一个开发分析模型来研究社交媒体用户注册动态的公司。Lin et al.[30]将博弈论应用于社交网络多媒体软件的指纹识别。Hu等人的[31]关注的是在线社交网络的问题,其中只允许单个用户访问她/他的数据,但不能提供任何机制来加强与多个用户相关的数据的隐私关注。这种关系如图6所示。
圆用于表示共享数据项c1的三个控制器的访问器空间;c2; andc3。该部分分为两部分:非冲突部分和冲突部分。段ns是不冲突的,而cs1到cs6是冲突的段。Cs1, cs2和cs3each表示一个隐私冲突;cs4, cs5和cs6与两个隐私冲突相关。通过博弈模型,考虑到控制器可能自私地追求自身利益最大化,提出了一个多方访问控制模型。针对冲突段中不可信访问器和可信访问器数量的三种不同情况,采用调整算法和数值分析方法对多方控制博弈进行了分析。
Azadjalal等人[32]在一种新型信任的基础上,结合Pareto优势概念和,提出了一种感知推荐系统社交网络。
(2)隐私策略
博弈论方法能够充分考虑各方利益,包括用户和攻击者。在解决隐私策略问题时,我们提出了一种解决方案,既能保证这些利益的安全,又能平衡隐私与服务质量的关系。Chen等[28]研究了用户的个人资料属性披露行为。具体来说,他们使用三种游戏理论方法模拟了社交网络的隐私和设置动态。
二用户游戏是指基本的、加权的进化游戏。这三个模型反映了不同因素对用户隐私选择的影响。White等人[27]提出了一种新的在线社交网络(OSN)建模方法,该方法基于一种创新的博弈论方法来分析某些不同的攻击场景。与其他模型不同的是,该分析考虑是否允许攻击者具有不同的动机和关于底层系统的不同数量的知识。在讨论中,游戏状态被共享、隐藏、隐藏和暴露。该模型利用马尔可夫博弈模型,帮助用户确定osn数据共享的最佳策略。Squicciarini等人还研究了社交网站中共享内容的隐私问题。他们使用了克拉克税收机制,提出了集体隐私管理问题的理论表述,并提出了基于著名的博弈论结果的解决方案。他们是第一个提出社交网络隐私保护机制的人。
这篇关于A Survey of Game Theory as Applied to Social Networks的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






