本文主要是介绍结合聚类的FW-GA混合算法在无人机森林火灾侦察任务分配中的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
An FW–GA Hybrid Algorithm Combined with Clustering for UAV Forest Fire Reconnaissance Task Assignment
原文地址:https://doi.org/10.3390/math11102400
An FW–GA Hybrid Algorithm Combined with Clustering for UAV Forest Fire Reconnaissance Task Assignment
摘要: 无人机森林火灾侦察任务的分配是一个高度复杂和大规模的问题。当前的任务分配方法努力在解决方案的速度和有效性之间取得平衡。提出了一种基于期望最大化(EM)聚类和多维背包模型(MKP)的两阶段集中无人机任务分配模型,用于森林火灾侦察任务分配。首先利用卫星携带的传感器获取火情信息。然后,采用基于高斯混合模型(GMM)的EM算法得到每个无人机的初始位置。最后,根据无人机的初始位置,将MKP应用于无人机任务分配。为了提高迭代速度,在烟花算法的基础上提出了一种改进的遗传算法(GA)。以四川凉山州森林火灾为背景进行了仿真,仿真结果表明,该任务分配模型能够快速、有效地解决大规模任务分配问题。此外,与传统遗传算法相比,FW-GA混合算法在求解时间、迭代收敛速度和求解效率方面都有很大的优势。与标准遗传算法相比,该算法的迭代时间减少了556%,目标函数值增加了1.7%。与GA-SA算法相比,其求解时间缩短了60倍。本文为解决未来大规模无人机任务分配问题提供了一种新的思路。
目录
- 一、介绍
- 二、森林火灾侦察模型描述
- 2.1初始化情景图
- 2.2 聚类分析
- 2.3 多维0-1背包问题
- 三、基于改进遗传算法结合聚类分析的无人机侦察任务分配策略
- 3.1基于GMM的电磁初始位置确定
- 3.1.1 基础理论
- 3.1.2 算法过程
- 3.1.3 确定每架无人机的初始位置
- 3.2 基于Fireworks算法的改进遗传算法求解多维0-1背包问题
- 3.2.1 基础理论
- 3.2.2 求解多维0-1背包问题的改进遗传算法
一、介绍
针对森林火灾侦察的需要,提出了一种两阶段无人机任务分配模型。该模型首先利用卫星携带的传感器数据对森林火灾进行数字化处理,然后利用基于GMM的EM算法得到各无人机的初始位置。利用数字火力模型和无人机的初始位置,建立了基于MKP的无人机任务分配模型。该模型极大地简化了模型的复杂性,同时避免了基于位置的严格局部分区问题,就像简单的k-means算法一样。遗传算法通常用于求解MKP问题,但其收敛速度慢,计算复杂度高,且容易陷入局部最优解。这使得有效地解决大规模背包问题具有挑战性。为了提高标准遗传算法的求解速度,提出了一种改进遗传算法来求解多目标函数。该混合算法改进了变异算子和交叉算子,具有自适应调整子代数量和变异概率的能力。该算法通过对小规模定向搜索和大规模广义优化的改进,提高了计算资源的利用率,增强了优化效果,从而提高了求解大规模背包问题的速度和分配效果。最后,基于所建立的模型,在2020年四川省凉山森林火灾的背景下进行了模拟实验。仿真结果表明,该模型能快速有效地解决火灾侦察任务分配问题。与标准遗传算法和其他改进算法相比,该混合算法具有更快的求解速度和更短的运行时间。本研究的贡献如下:
- 本文提出了一种新的任务分配模型,以解决无人机在森林火灾监测中复杂、大规模侦察任务的挑战。首先,本文引入了GMM的EM算法来确定任务点聚类的中心,并将其设置为每个无人机的初始位置,而不是使用聚类算法简单地根据位置分配任务 。然后,基于每个无人机的初始位置,创新性地利用MKP模型解决任务分配问题;每架无人机被视为一个背包,任务被视为有价值的物品。这巧妙地实现了uav的任务分配。
- 受烟火算法中火花数量和半径的启发,对遗传算法中的变异和交叉算子进行了改进,实现了变异概率和变异后代数量的动态调整。仿真实验结果表明,该算法具有较快的收敛速度和较好的优化性能,在求解速度和优化效果上实现了双重提高。
- 以四川凉山森林火灾为例,基于卫星遥感信息,进行了无人机任务分配的模拟试验。实验验证了模型和算法的可行性和优越性,实验方法和结果为未来无人机在灾区的侦察任务分配提供了参考。
二、森林火灾侦察模型描述
为了有效地进行森林火灾侦察,需要建立无人机火灾侦察任务分配模型。首先,基于卫星传感器获取的火点信息,对森林火灾进行数字化建模;然后,利用GMM逼近火力点分布图,将每个高斯分布的二维期望坐标设置为每个无人机的初始位置;最后,将无人机视为背包,并将火力点视为物品。采用MKP模型解决无人机侦察任务分配问题。每个无人机的任务因此被确定,以及在每个“背包”的火力点。无人机侦察任务分配模型的详细流程如图1所示。
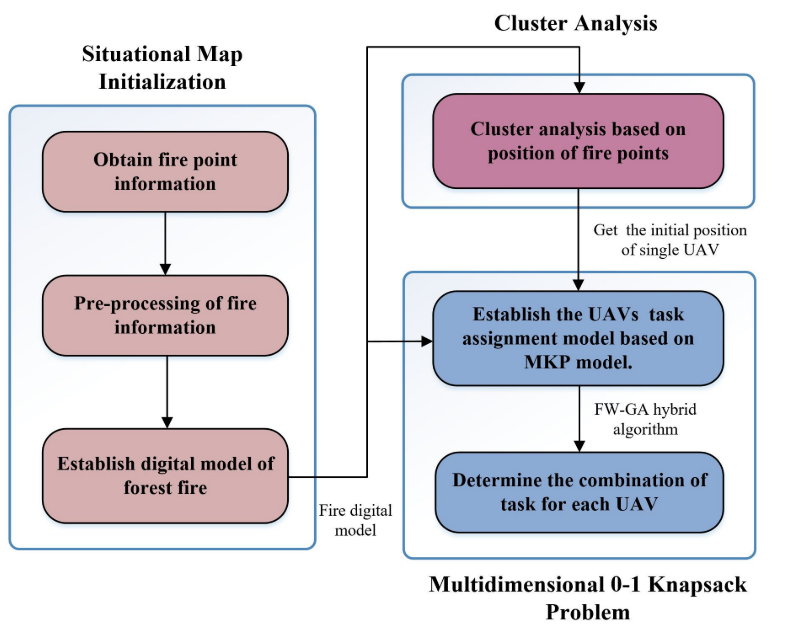
2.1初始化情景图
2.2 聚类分析
基于火点位置信息(xj, yj),利用聚类算法对火点进行分类。将相邻火点划分为同一“簇”,得到火点簇Mj。此外,集群数等于无人机数量m:
M j = [ T ( k j ) ] , ( 1 ≤ k j ≤ 886 , 1 ≤ j ≤ m ) \boldsymbol{M}_{j}=\left[\boldsymbol{T}\left(k_{j}\right)\right],\left(1 \leq k_{j} \leq 886,1 \leq j \leq m\right) Mj=[T(kj)],(1≤kj≤886,1≤j≤m)
根据划分的聚类,得到各聚类c的中心点:
c = [ ( x c 1 , y c 1 ) , ( x c 2 , y c 2 ) , … … , ( x c j , y c j ) , … … , ( x c m , y c m ) ] \boldsymbol{c}=\left[\left(x c_{1}, y c_{1}\right),\left(x c_{2}, y c_{2}\right), \ldots \ldots,\left(x c_{j}, y c_{j}\right), \ldots \ldots,\left(x c_{m}, y c_{m}\right)\right] c=[(xc1,yc1),(xc2,yc2),……,(xcj,ycj),……,(xcm,ycm)]
2.3 多维0-1背包问题
图5描述了无人机的任务分配过程。依次解决每个无人机的任务分配问题,从而有利于整个无人机任务分配问题的解决。在获取每个无人机的初始位置后,可将群体中个体无人机的任务分配问题建模为一个多维的0-1背包问题。该问题将每架无人机视为一个具有飞行距离、侦察信息存储空间等多个“容量”限制维度的多约束背包。将每个火点视为背包中一个不同值和体积的物品,每个物品的值代表该火点的等级值,每个物品所占的体积代表无人机侦察该火点所需的电池消耗和存储空间。目标是在满足无人机飞行距离和存储容量约束的条件下,找到秩值最高的火力点组合
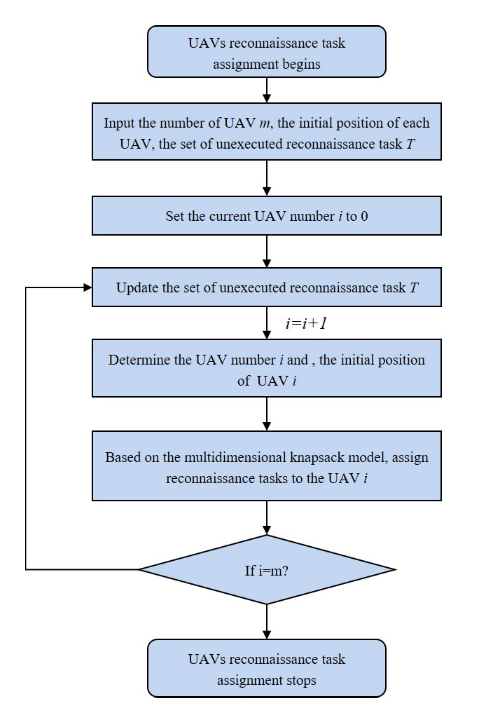
无人机约束:
- 现代无人机通常由锂电池供电。它们通常携带重型设备执行侦察任务,这极大地限制了它们的飞行距离。因此,分配给单个无人机和无人机本身的火力点之间的距离之和必须受到限制,以满足无人机的持久极限。
- 为了避免重复侦察,每个新的任务点必须是一个迄今未侦察的点。
- 较高的优先点需要对任务的有效性进行更详细的侦察。因此,对于优先级较高的点,需要仔细侦察,所产生的侦察信息将消耗更多的存储空间。因此,单架无人机的存储空间也是一个重要的限制。
- 为了缩短每架无人机执行任务的时间,以及便于后续每架无人机的路径规划,需要限制分配给每架无人机的火力点总数。
建立约束的数学模型如下:
在大多数研究中,任务区域被划分为多个子区域,然后在每个子区域内分配任务,这导致了每架无人机只能在一定划定的区域内执行侦察任务的问题。为了更好地平衡全局考虑,将每个无人机的距离约束设置为无人机与指定侦察点之间的距离之和 。因此,每一架无人机不仅可以在离自己更近的地区执行任务,而且还可以在有更多优先任务的地区,在离其他无人机更近的地区协助侦察。
∑ i ∈ N j ( x i − x c j ) 2 + ( y i − y c j ) 2 ≤ L max \sum_{i \in N_{j}} \sqrt{\left(x_{i}-x c_{j}\right)^{2}+\left(y_{i}-y c_{j}\right)^{2}} \leq L_{\max } i∈Nj∑(xi−xcj)2+(yi−ycj)2≤Lmax
式(4)中,Nj为分配给无人机j的火力点索引数组,xi、yi为火力点i在集合T中的横坐标、纵坐标,xcj、ycj为无人机j初始位置的横坐标、纵坐标,Lmax为距离限制。该方程表示所有指定火力点到无人机j初始位置的距离之和小于Lmax。如图6所示,当无人机j被分配4个侦察点时,该约束可表示为
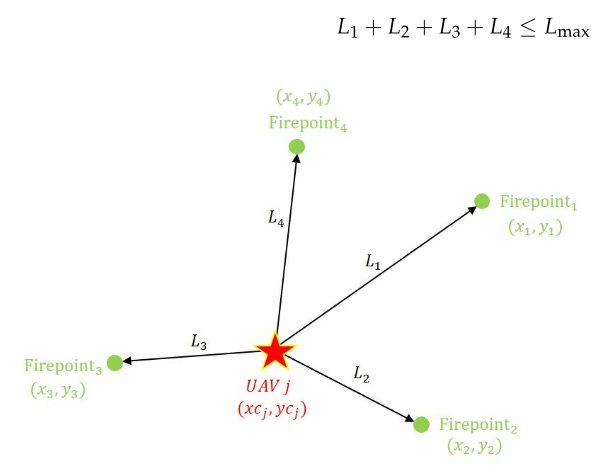
-
分配给无人机的火点应该是以前没有被探测到的点。定义一个886维向量S,如果火点i未被探测到,则S(i) = 1;否则,S(i) = 0。因此,如果没有对火点进行侦察,我们可以得到:
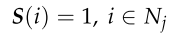
-
每个无人机的存储空间约束。定义一个向量P表示每个火点所消耗的存储空间。火力点的优先级越高,生成的侦察信息量越大,存储空间的消耗就会大大增加。因此,定义参数P与火点优先级的平方线性相关。P的定义如下:
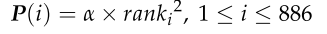
P(i)为火点i的存储空间消耗,α为系数,为计算方便,α = 0.01。
因此,每架无人机的存储空间约束可以表示为:
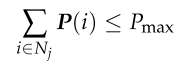
-
每个无人机指定火力点的数量限制。
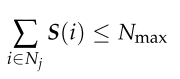
Nmax为每架无人机分配的射击点数量约束。 -
目标函数。根据上文中对项目值的定义,将分配给每架无人机的所有火力点的优先级之和定义为MKP的目标函数:
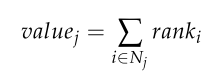
valuej为无人机j的目标函数值,ranki和Nj为前面定义的。
三、基于改进遗传算法结合聚类分析的无人机侦察任务分配策略
在前一节建立的模型的基础上,采用基于高斯混合模型的EM算法对火点分布进行了近似计算。高斯混合模型包含m(无人机群中单个无人机的数量)二维高斯分布。利用EM算法得到二维高斯期望,将无人机的初始位置设为期望。自1998年P. C.等人[31]首次提出遗传算法以来,遗传算法已被广泛应用于求解多维0-1背包。为了进一步加快求解速度,提出了一种fw - ga混合算法来解决MKP问题,并在算法中引入了基于二元精英对立的学习机制[32]和贪婪选择算子。从而得到了每架无人机的最优射击点组合。
3.1基于GMM的电磁初始位置确定
3.1.1 基础理论
GMM(高斯混合模型)是指多个具有一定权重的高斯混合模型的组合。理论上,GMM可以拟合任何类型的分布。在这个问题中,GMM由m个二维正态分布组成,其中每个二维高斯分布N(X|µk, Σk)称为一个分量。数学表达式如下:
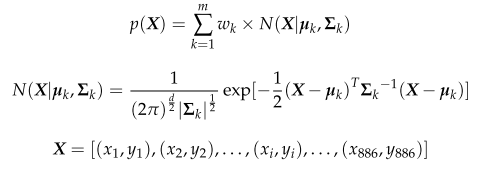
wk是高斯分布k的权值;µk为高斯分布k的均值;Σk为高斯分布k的方差;X为火力点坐标集合,其中xi、yi定义如式(1)所示;d是X的维数,这里d = 2。另外,wk满足m∑k=1 wk =1。
这里,将wk视为高斯模型k被选中的概率。此外,引入一个新的m维变量z(m定义为单架无人机数量),其中z(k)只有两个值,0或1:
p ( z ( k ) = 1 ) = w k , z ( k ) = { 0 , 1 } , 1 ≤ k ≤ m ∑ m z ( k ) = 1 , z ( k ) = { 0 , 1 } \begin{array}{l} p(\boldsymbol{z}(k)=1)=w_{k}, \boldsymbol{z}(k)=\{0,1\}, 1 \leq k \leq m\\ \sum^{m} z(k)=1, z(k)=\{0,1\} \end{array} p(z(k)=1)=wk,z(k)={0,1},1≤k≤m∑mz(k)=1,z(k)={0,1}
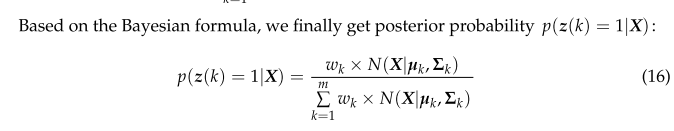
利用EM算法对各参数进行似然估计。EM算法可分为两个步骤。第一步是根据现有参数计算后验概率。第二步是根据后验概率的值计算新参数。重复迭代过程,得到GMM的参数值。w,µ,Σ这三个参数的获取方法相对简单,本文不作详细阐述。
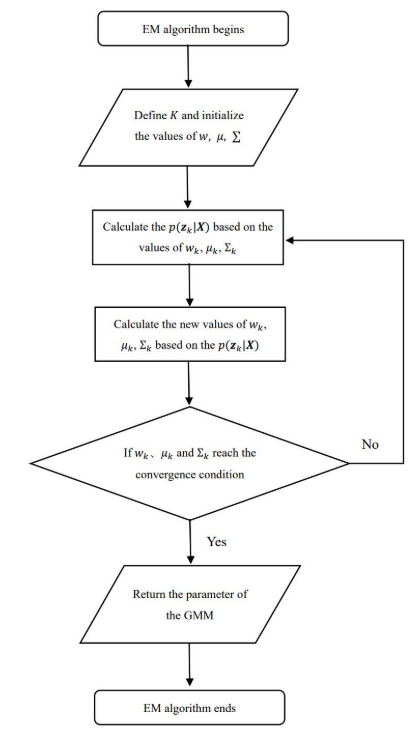
3.1.2 算法过程
3.1.3 确定每架无人机的初始位置
本文假设无人机数量m为4个;因此,GMM由四个高斯分布组成。通过EM算法的不断迭代,找到了每个高斯分布的期望二维坐标。预期坐标被认为是火点密度最高的位置;因此,µk设为无人机k的初始位置。
3.2 基于Fireworks算法的改进遗传算法求解多维0-1背包问题
3.2.1 基础理论
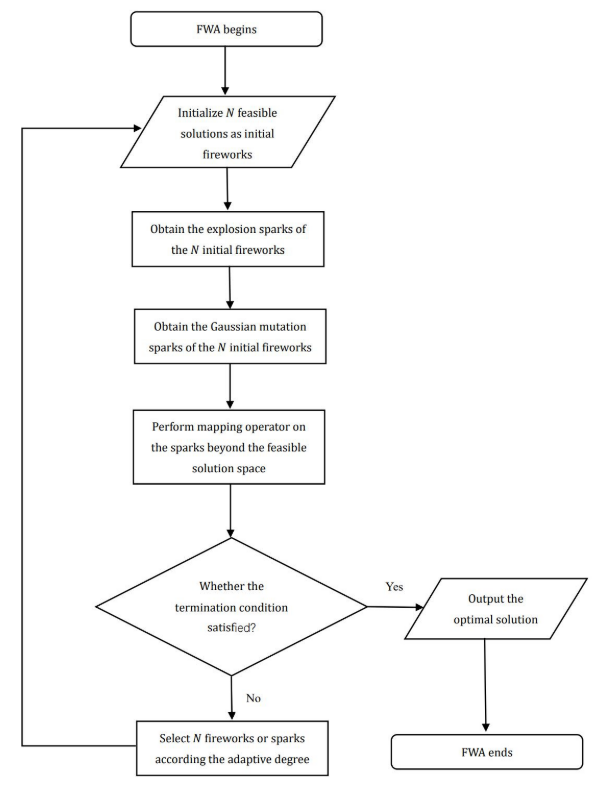
受烟花爆炸过程的启发,Tan和Zhu[22]在2010年提出了一种全新的群智能算法FWA。FWA是求解优化问题的一种非常有效的方法。FWA认为复杂而巨大的解决方案空间就像一个漆黑的夜空和烟花,代表了一个可行的解决方案。在黑暗的夜空中爆炸并产生大量火花的过程被认为是在可行解周围的解空间中寻找最优解的过程。夜空中的烟花不断地在夜空中“爆炸”,在解空间中寻找最优解。
该算法主要由爆炸算子、高斯变异算子、映射算子和选择算子组成。算法中算子的性能直接决定了FWA的优化性能。
- 爆炸操作:
爆炸操作是fwa的核心,也是从初始烟花中产生爆炸火花以及在解空间中寻找最优解的主要方法。根据烟花的自适应程度和烟火种群中其他烟花的自适应程度,确定一个烟花的爆炸半径和爆炸火花数。它可以合理分配资源,平衡局部搜索能力和全局搜索能力。如果烟花具有较高的适应度,那么在它的邻域内得到全局最优解的可能性就会高得多。这样,烟花就会被分配更多的资源,产生更多的火花,从而在其周围找到全局最优解。对于适应程度较低的烟花,分配的资源较少。
烟花i的爆炸半径Ai和爆炸火花数Si可计算为:
A i = A ^ × f max − f i + ε ∑ i = 1 N ( f max − f i ) + ε A_{i}=\hat{A} \times \frac{f_{\max }-f_{i}+\varepsilon}{\sum_{i=1}^{N}\left(f_{\max }-f_{i}\right)+\varepsilon} Ai=A^×∑i=1N(fmax−fi)+εfmax−fi+ε
fmax为最大适应度,N为烟花种群中的个体数,ε为小数值,以保证分母值不为0,Aˆ为调节爆炸半径的调节系数。
S i = S ^ × f i − f min + ε ∑ i = 1 N ( f i − f min ) + ε S_{i}=\hat{S} \times \frac{f_{i}-f_{\min }+\varepsilon}{\sum_{i=1}^{N}\left(f_{i}-f_{\min }\right)+\varepsilon} Si=S^×∑i=1N(fi−fmin)+εfi−fmin+ε
式(18)中,fmin为最小适应度,ˆS为调整爆炸火花数的调整系数。其余参数含义与式(17)相同。
为了防止低适合度烟花产生的火花太少,高适合度烟花产生的火花太多,在以下烟花算法中限制产生的火花数量:
S i = { round ( a × S ^ ) , S i < a × S ^ round ( b × S ^ ) , S i > b × S ^ , a < b < 1 round ( S i ) , others S_{i}=\left\{\begin{array}{ll} \operatorname{round}(a \times \hat{S}), & S_{i}<a \times \hat{S} \\ \operatorname{round}(b \times \hat{S}), & S_{i}>b \times \hat{S}, a<b<1 \\ \operatorname{round}\left(S_{i}\right), & \text { others } \end{array}\right. Si=⎩ ⎨ ⎧round(a×S^),round(b×S^),round(Si),Si<a×S^Si>b×S^,a<b<1 others
其中a和b是两个常系数,“round”表示舍入函数。
- 高斯突变算子
为了避免优化过程中的局部最优问题,增加火花种群的多样性,在产生爆炸火花的过程中引入高斯变异。高斯突变的具体数学表达式如下:
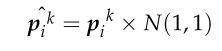
pk i为烟花种群中烟花 i 的k维编码值,N(1,1)为均值为1、方差为1的一维高斯分布。 - 选择操作
这里的选择操作符类似于GA中的选择操作符。我们将在下一节详细介绍它。
3.2.2 求解多维0-1背包问题的改进遗传算法
标准遗传算法存在计算复杂度高、收敛速度慢、容易陷入局部最优解等缺点。这些问题在林火侦察工作中是不可接受的。火情侦察任务分配问题需要较快的求解速度,才能更快、更有效地进行火情侦察,从而减少经济损失。因此,标准遗传算法明显难以满足火灾侦察任务分配问题求解速度和优化的要求。在烟火算法的基础上,提出了一种改进的遗传算法,以平衡其求解速度和优化程度,解决火灾侦察任务分配问题。同时,引入精英对抗学习和贪婪选择算子,进一步提高算法的收敛速度和优化能力。
FW-GA混合算法主要受FWA中火花半径和火花数的启发,对其变异和交叉算子进行了改进。当个体适应度在种群中较高时,更有可能在其附近找到全局最优解;因此,在附近较小的解决方案空间中产生更多的后代。反之,如果适应度较低,则在附近找到全局最优解的概率较低;因此,在附近更大的范围内产生的后代更少,从而探索更大的解决方案空间。该混合算法兼顾了局部和全局优化能力,与标准遗传算法相比,大大提高了计算资源的利用率,提高了求解速度和优化效率
-
编码规则
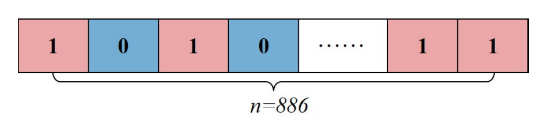
混合遗传算法采用二进制编码原理,如图10所示。在该编码方案中,每条染色体代表一个可行解,染色体中基因片段数n表示需要分配的侦察任务数。其中,二进制编码为1表示无人机应执行相应的侦察任务,二进制编码为0表示无人机不应执行该任务。这种编码策略在科学研究中得到了广泛的应用,并被证明是有效的
- 初始化
由于所选的火力侦察背景总共包括n个火点,由计算机生成一个随机的N × n的二进制矩阵,其中N为人口规模。该矩阵表示一架无人机的N个不同解,每个解包含886条信息,对应886个需要分配的任务。 -
修正操作
这里引入利润密度的概念,以飞行范围约束为例,解释利润密度的概念:
D i = L max × rank i ∑ i ∈ N j ( x i − x c j ) 2 + ( y i − y c j ) 2 D_{i}=\frac{L_{\max } \times \operatorname{rank}_{i}}{\sum_{i \in N_{j}} \sqrt{\left(x_{i}-x c_{j}\right)^{2}+\left(y_{i}-y c_{j}\right)^{2}}} Di=∑i∈Nj(xi−xcj)2+(yi−ycj)2Lmax×ranki
Di为利润密度,Lmax为式(4)所定义的极限值。当出现可行空间以外的解时,对于利润较低的个体,通过将对应任务点的基因片段设置为0,将解逐一延展。重复这个过程,直到种群中的所有个体都在可行解空间内。 -
适应度计算
目标函数:
value j = ∑ i ∈ N j rank i \text { value }_{j}=\sum_{i \in N_{j}} \operatorname{rank}_{i} value j=i∈Nj∑ranki -
精英对抗性学习操作
在这里,个人的适合度大于95%的最大适合度在流行集可以被认为是精英个人。

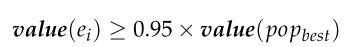
对于多维0-1背包问题,二进制编码反解可表示为:
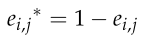
就是将染色体的每一位0 1 互换
根据二元精英对立学习策略,将存在差异的维度倒转以获得新的个体。
反解的步长:
r E = ceil ( rand ∗ L E + ε ) r^{E}=\operatorname{ceil}\left(\operatorname{rand} * L^{E}+\varepsilon\right) rE=ceil(rand∗LE+ε)
– LE:反解的维度数
– ceil: 取整函数
– ε:极小数
e3,885∗ = 1 − e3,885 and e3,886∗ = 1 − e3,886 , rE = 2 and LE = 3,
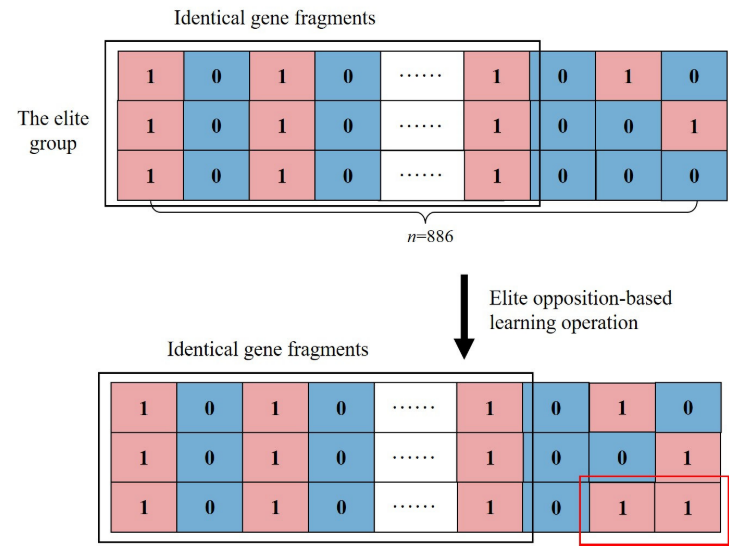
-
突变算子
在标准遗传算法中,以相同的概率随机突变不同的基因编码位置来实现突变。这种方法可以在一定程度上增加种群的遗传多样性。但是,如果在迭代结束时种群适应度普遍较高,而突变概率保持不变,则可能会减慢迭代速度,使迭代难以收敛到全局最优解。在标准遗传算法中,每一个父母在突变后通常产生一定数量的后代。众所周知,高适合度的双亲产生高适合度后代的概率一般较高,而低适合度的双亲产生低适合度后代的概率则较低。如果每个父代产生相同数量的后代,会浪费大量的计算资源,可能会影响最终的优化结果。
智能调节遗传算法的变异概率和后代数量是优化遗传算法、更快更好地解决多维01背包问题的关键。在爆炸半径和爆炸火花数概念的基础上,对传统遗传算法中的变异算子进行改进,以求解多维0-1背包问题
由式(26)可得到一个动态可调的突变概率pi m
p m i = A ^ × f max − f i + ε ∑ i = 1 N ( f max − f i ) + ε 886 p_{m}^{i}=\frac{\hat{A} \times \frac{f_{\max }-f_{i}+\varepsilon}{\sum_{i=1}^{N}\left(f_{\max }-f_{i}\right)+\varepsilon}}{886} pmi=886A^×∑i=1N(fmax−fi)+εfmax−fi+ε
A^为调整突变概率的调整系数.
在确定每个父母的突变概率后,对每个基因片段进行等概率突变。

其中第一个和第二个基因片段表示基因突变成功。
对以往的fireworks算法进行分析发现,当个体适应度较高时,会降低变异概率,缩小搜索范围;当突变概率较低时,会增加突变概率,扩大搜索半径,在更大的空间内寻找最优解
同时,为了更好地分配计算资源,父代i所产生的后代数量:
n u m m i = ceil ( S ^ × f i − f min + ε ∑ i = 1 N ( f i − f min ) + ε ) num_{m}{ }^{i}=\text { ceil }\left(\hat{S} \times \frac{f_{i}-f_{\min }+\varepsilon}{\sum_{i=1}^{N}\left(f_{i}-f_{\min }\right)+\varepsilon}\right) nummi= ceil (S^×∑i=1N(fi−fmin)+εfi−fmin+ε)
– Nummi表示亲本 i 产生的后代数量,
– Sˆ也是一个调整后代数量的调整系数
– 后代数量下限和上限的定义与FWA中烟花数量下限和上限的定义相同。
可以确定后代的数量是由父母的适合度决定的。具有较高适应度的父节点可能更接近全局最优解,为其分配更多的计算资源来搜索最优解。相反,适合度较低的父母更有可能离它很远
-
交叉操作
在标准遗传算法中,交叉点和交叉长度是随机的,交叉概率一般是确定的,这就导致了与变异算子相同的困境:计算资源的不合理分配。
父节点的交叉长度和交叉概率:
l i = ceil ( A ^ × f max − f i + ε ∑ i = 1 N ( f max − f i ) + ε ) p c i = l i n \begin{array}{c} l_{i}=\operatorname{ceil}\left(\hat{A} \times \frac{f_{\max }-f_{i}+\varepsilon}{\sum_{i=1}^{N}\left(f_{\max }-f_{i}\right)+\varepsilon}\right) \ \end{array}p_{c}{ }^{i}=\frac{l_{i}}{n} li=ceil(A^×∑i=1N(fmax−fi)+εfmax−fi+ε) pci=nli
N是染色体中基因片段的数量。与变异算子相似,交叉长度和交叉概率与父节点的适应度相关。对于适应度高的个体,距离全局最优解的距离可能更短;因此,交叉长度和交叉概率的值不必太大;相反,采用较高的交叉概率和较长的交叉长度在更大的空间内搜索最优解。第二,需要确定每对父母产生的后代数量,这里也采用了类似于突变算子的策略:
num c i = ceil ( S ^ × f i − f min + ε ∑ i = 1 N ( f i − f min ) + ε ) \operatorname{num}_{c}^{i}=\text { ceil }\left(\hat{S} \times \frac{f_{i}-f_{\min }+\varepsilon}{\sum_{i=1}^{N}\left(f_{i}-f_{\min }\right)+\varepsilon}\right) numci= ceil (S^×∑i=1N(fi−fmin)+εfi−fmin+ε)
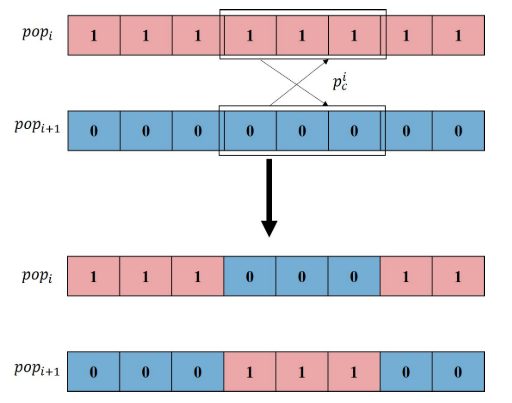
-
选择操作
标准遗传算法采用轮盘赌轮盘选择方法为下一代选择后代。为了加快迭代速度,引入贪心策略对选择算子进行改进。如图14所示,每一代中按适应度排名的顶端ceil(N/10)(其中ceil()为整数函数)的个体被保留到下一代,而没有基于概率的选择。同时,采用轮盘赌轮盘选择方法,从剩余的种群中选择N-ceil(0.1 ×N)个体,从而保证每一代所选择的后代数量始终为n。
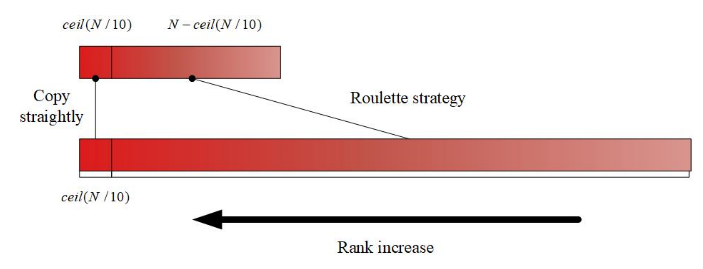
-
终止条件确定
本文的GA-SA算法有两个终止条件。第一个条件是,如果当前代种群与前代种群的最大适应度值之差与当前代种群的最大适应度值之比小于eps,则迭代停止。第二个条件是,如果算法达到预设的迭代次数,则迭代停止。
这篇关于结合聚类的FW-GA混合算法在无人机森林火灾侦察任务分配中的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




