Week1：[任务三] 第二节 autograd与逻辑回归

【目录】

• 自动求导系统

• 逻辑回归 

1、自动求导系统

• torch.autograd.backward()方法

张量中的y.backward方法实际调用的是torch.autograd.backward()方法

同一个张量反向传播的迭代，需要将y.backward(retain_graph)设置为True

• tensors为用于求导的张量，如loss；loss.background()，用于对requires_grad为true的叶子节点进行梯度自动求解；
• retain_graph用于保存计算图，因为pytorch为动态图机制，每次自动求导运算后都会释放掉，如果想要迭代使用计算图，需要将其置为true；
• create_graph创建导数的计算图，通常用于高阶求导，如二阶、三阶；
• grad_tensors：多梯度权重设置，当有多个loss需要计算梯度时，需要设置各个loss的权重；

# retain_graph用处不多，一般迭代计算梯度，将loss表达式和loss.back一同放入for循环中即可

# ====================================== retain_graph ==============================================
flag = True
# flag = False
if flag:w = torch.tensor([1.], requires_grad=True)x = torch.tensor([2.], requires_grad=True)a = torch.add(w, x)b = torch.add(w, 1)y = torch.mul(a, b)y.backward(retain_graph=True)print(w.grad)y.backward(retain_graph=True)print(w.grad)

# grad_tensors多权重求梯度

#多权重求loss梯度
import torchw = torch.tensor([1.],requires_grad = True)
x = torch.tensor([2.],requires_grad = True)a = torch.add(w,x)
b = torch.add(w,1)
y0 = torch.mul(a,b)
y1 = torch.add(a,b)loss = torch.cat([y0,y1],dim = 0)#拼接
print(loss)
grad_tensors = torch.tensor([1.,1.])loss.backward(gradient = grad_tensors)#y0对w的梯度*权重+y1对w的梯度*权重
print(w.grad)#运行结果输出
runfile('C:/Users/cheny/Desktop/untitled0.py', wdir='C:/Users/cheny/Desktop')
tensor([6., 5.], grad_fn=<CatBackward>)
tensor([7.])

• torch.autograd.grad()方法

output为Y，input为X，求取的是Y对X的偏导，即求X的梯度

下划线表示原地操作in-place操作，在原始地址上直接进行改变，例如a+=1，a的地址没有变化

#求高阶导数，create_graph = True设置
import torch
x = torch.tensor([3.],requires_grad=True)
y = torch.pow(x,2)#y=x²grad_1 = torch.autograd.grad(y,x,create_graph=True)#一阶导数为y=2x=6
print(grad_1)grad_2 = torch.autograd.grad(grad_1[0],x)#二阶导数为y=2
print(grad_2)#运行结果输出
runfile('C:/Users/cheny/Desktop/untitled0.py', wdir='C:/Users/cheny/Desktop')
(tensor([6.], grad_fn=<MulBackward0>),)
(tensor([2.]),)

叶子张量不能执行in-place操作，因为前向传播保存的地址数据不能有变化，否则反向传播会出错

注意：

• 梯度在自动求导过程中不会自动清零，每次都会自动叠加上去，需要手动清零。e.g w.grad.zero_()进行清零
• 依赖于叶子结点的结点，requires_grad默认为True(是否需要梯度)
• 叶子结点不可执行in-place

#梯度不会自动清零，需要手动清零
import torchw = torch.tensor([1.],requires_grad = True)
x = torch.tensor([2.],requires_grad = True)for i in range(2):a = torch.add(w,x)b = torch.add(w,1)y = torch.mul(a,b)y.backward()print(w.grad)#w.grad.zero_() #手动清空#运行结果输出
runfile('C:/Users/cheny/Desktop/untitled0.py', wdir='C:/Users/cheny/Desktop')
tensor([5.])
tensor([10.])

2、逻辑回归

• sigmoid函数的作用就是将输入的数据映射到0-1之间，输出的Y就能用来做二分类

• 逻辑回归是在线性回归的基础上增加了一个激活函数，增加激活函数是为了更好的描述，用概率来描述，同时更好的拟合，避免梯度消失现象

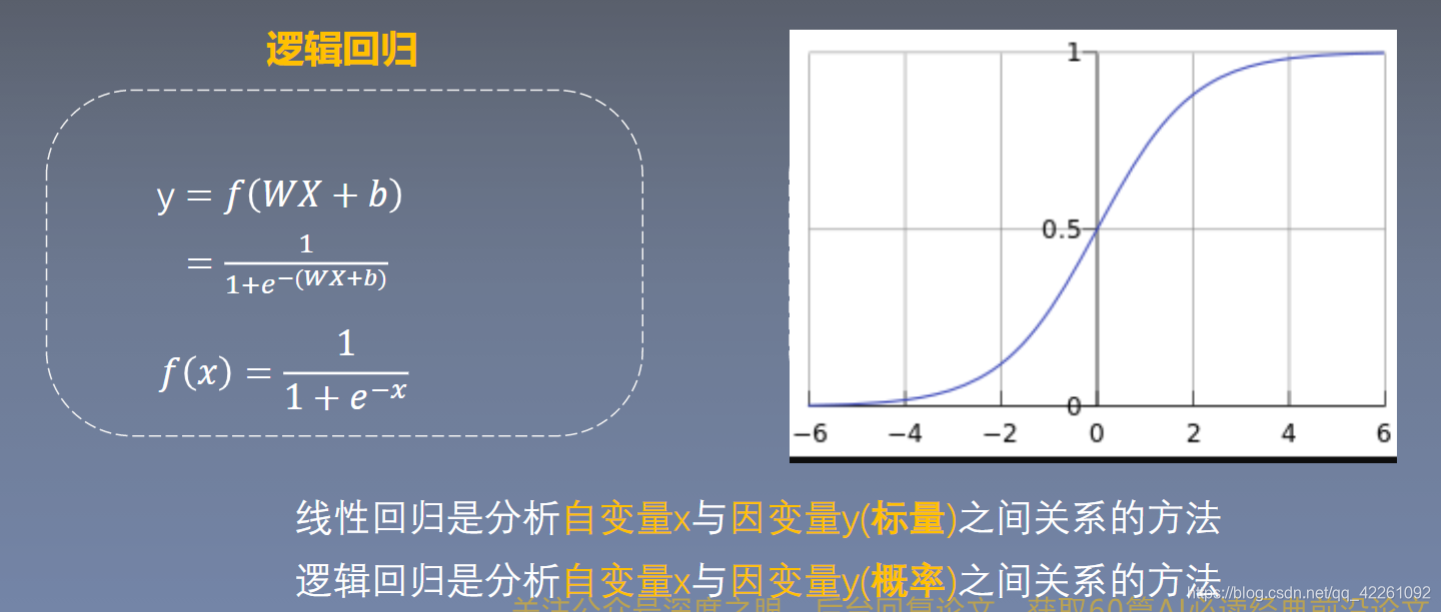
• 逻辑回归又叫对数几率回归，几率即为y/1-y（概率取值y除以1-y）表示样本x为正样本的可能性。线性回归用wx+b去拟合Y，而逻辑回归是用wx+b去拟合一个对数几率

• 机器学习训练步骤（五步）