维特比译码器(Viterbi Decoder)硬件架构(一)--卷积码及编解码算法介绍

本文主要是介绍维特比译码器(Viterbi Decoder)硬件架构(一)--卷积码及编解码算法介绍，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 卷积码(convolution code)

卷积码在无线通信里用的非常广泛，通常卷积码编码器开始工作前都要进行初始化，按编码器的初始状态不同可以分为两类：

1.1 末尾补零卷积码(Tail-bits)：

通常卷积码编码器开始工作时都要进行初始化，编码开始前将编码器的所有寄存器单元都进行清零处理。而在编码结束时，需要添加0到码流末尾(Tailed Termination)，使编码器状态归零, 这即是末尾补零卷积码。相对于编码比特而言，添加的末尾比特增加了编码开销。

1.2 咬尾卷积码(Tail biting)：

咬尾卷积编码是一种特殊的卷积编码，它通过将编码器的移位寄存器的初始值设置为输入流的末尾比特值，使得移位寄存器的初始和最终状态相同。编码器开始工作时要进行特殊的初始化，将输入信息比特的最后m个比特依次输入编码器的寄存器中，当编码结束时，编码器的结束状态与初始状态相同。由于这个编码方法没有出现尾比特，因此称为咬尾编码。
咬尾编码减少了尾比特的编码开销。对于咬尾编码方法，在译码过程中，由于编码器的初始状态和结尾状态是未知的，因此就需要增加一定的译码复杂度，才能确保好的译码性能。和普通的卷积编码相比，咬尾的方案最大的优点是克服了编码时的码率损失，并且适合迭代译码，不过付出的代价是译码复杂度的增加。

2. 编码过程

通常以 (n, k, L) 来描述卷积编码，其中：
• k 表示编码器的 输入码元数
• n 表示编码器的 输出码元数
• L表示编码器的 约束长度
由输入的 k 个信息比特，得到 n 个编码结果，所以 编码效率 = k/n。约束长度 L 的意思是，编码结果不仅取决于当前输入的 k 比特信息，还取决于前 (L-1) 段时间内的信息位。在 k = 1 的条件下，编码器需要的移位寄存器级数 m = L - 1。例如，LTE 标准中编码器的结构如下图所示：

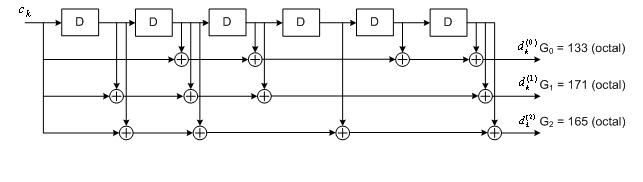
图中的 G1，G2, G3 是生成式。

假设输入的比特流为 c1, c2, c3, ... 得到的编码结果为 d1, d2, d3, ...

2.1 对于tail-bits卷积码：

其中移位寄存器 D 从左到右一次是 S0, S1, ... S5。对其初始化时，S0 = 0, S1 = 0, ... S5 = 0。
进行编码时，有抽头的寄存器之间进行模 2 加法（即异或）运算。每次对一个输入信息完成编码之后，移位寄存器右移一位，抛弃最右端的移位结果，采用前一个输入作为最左端的信息位。
当最后的码流比特进行编码完之后，编码器需要额外输入6个bit 0，使其恢复到初始状态，同时将额外产生的6bit输出放进输出码流末尾，一同发送到接收端。

2.2 tail-biting卷积码

其中移位寄存器 D 从左到右一次是 S0, S1, ... S5。对其初始化时，S0 = Ck-1, S1 = Ck-2, ... S5 = Ck-6。
进行编码时，有抽头的寄存器之间进行模 2 加法（即异或）运算。每次对一个输入信息完成编码之后，移位寄存器右移一位，抛弃最右端的移位结果，采用前一个输入作为最左端的信息位。
当最后的比特进行编码完之后，寄存器又回到了设定的初始状态，就像一条蛇咬住了自己的尾巴，所以称为咬尾 Tail Biting。

2.3 tail-bits和tail-biting的优缺点

tail-bits的优点：（1）开始状态和结束状态对解码器来说是已知的，解码复杂的相对低些。 2）bit error rate (BER) 不受末尾补零操作的影响
tail-bits的缺点：（1）由于额外增添了一些bit需要发送，降低了传输码率。（2）额外增添的bit需要消耗额外的发送时间，轻微降低了 Eb/No, Eb是energy-per-bit, No是noise-power0spectral-density。
tail-biting的优点：（1）码率不受影响。（2）不影响bit error rate (BER) 。
tail-biting的缺点：（1）初始状态对解码器不可知，需要解码器花时间训练，来找到正确的开始状态和初始traceback状态，这样便增加了解码延时（2）解码器复杂的相对较高。