西北农林科技大学2020年算法分析与设计实验一——贪心法求解会场安排问题 基于分治法的循环日程表算法

实验1

贪心法求解会场安排问题 & 基于分治法的循环日程表算法

实验内容

本实验要求基于算法设计与分析的一般过程（即待求解问题的描述、算法设计、算法描述、算法正确性证明、算法分析、算法实现与测试），使用贪心法求解会场安排问题以及利用分治法的循环日程表算法，以期从实践中理解分治法的思想、求解策略及步骤。（有余力者，鼓励挑战n≠2k的情形的循环日程表问题，以及贪心法与分治法的其它应用实例）

实验目的

1. 理解贪心法的核心思想以及分治法求解过程；
2. 理解分治法的核心思想以及分治法求解过程。

环境要求

无特别要求。算法实现可以自由选择C, C++, Java，甚至于其他程序设计语言。

本次选用c++

实验结果

贪心法求解会场安排问题的解

问题描述

• 设有n个会议的集合C={1,2,…,n}，其中每个会议都要求使用同一个资源（如会议室），而在同一时间内只能有一个会议使用该资源。
• 每个会议i都有要求使用该资源的起始时间bi和结束时间 e_i，且 b_i < e_i 。如果选择了会议i使用会议室，则其在半开区间[b_i, e_i)内占用该资源。
• 如[b_i, e_i)与[b_j, e_j)不相交，则称会议i与j是相容的。
• 会场安排问题要求：在所给的会议集合中选出最大的相容活动子集，亦即尽可能多地选择会议来使用资源

几种贪心策略

• 选择最早开始时间且不与已安排会议重叠的会议：
  但如果会议的使用时间无限长，如此选择策略就只能安排1个会议来使用资源。不可行。
• 选择使用时间最短且不与已安排会议重叠的会议：
  但如果会议的开始时间最晚，如此选择策略也就只能安排1个会议来使用资源。不可行。
• 选择最早结束时间且不与已安排会议重叠的会议：
  如果选择开始时间最早且使用时间最短的会议，较为理想。而此即结束时间最早的会议。可行。

解题思路

1. 对活动进行排序，开始时间越早排在越前面，如果两个活动时间相同，则结束时间越早的排在越前面
2. 开始时间最早和持续时间最短的优先安排会场，并记录会场号，
3. 其余活动的开始时间大于或等于已安排活动的结束时间的安排在同一会场，
4. 若某活动的开始时间小于已经安排了会场的活动的结束时间，则安排在另一会场，记录会场号。
5. 依次循环，直到所有活动均被安排

求解策略按照步骤

• 步骤1：初始化，并按会议结束时间非减序排序。
  
  (我选用的是快速排序(自定义排序))
  定义两个数组，开始时间存入数组start_time，结束时间存入数组end_time中；
  按照结束时间的非减序排序，start_time需做相应调整；
  集合A存储解。如果会议i在集合A中，当且仅当其被选中。
  
  
  
• 步骤2：根据贪心策略，做第一次贪心选择。
  
  首令A[1] = 1；
  
  
  
• 步骤3：依次扫描每一个会议，直至所有会议检查完毕。
  
  如果会议i的开始时间不小于最后一个选入A中的会议的结束时间，则将会议i加入A中；
  否则，放弃并继续检查下一个会议与A中会议的相容性。
  

步骤2：

算法设计，包括算法策略与数据结构的选择；

算法设计

---

首先用快速排序按照结束时间进行非降序排序

然后设置flag进行安排，得到sum的值即为最终结果

步骤3：

描述算法。希望采用源代码以外的形式，如伪代码、流程图等；

伪代码

while:n-count>0:
do
int:cur = 0;
for:i=0 to n do i++:
doif meeting[i].start_time > cur && meeting[i].flag == 0:domeeting[i].flag = 1;cur = meeting[i].end_time;count++;done
donesum++;
done

步骤4：

算法的正确性证明。需要这个环节，在理解的基础上对算法的正确性给予证明；

最优子结构性质的证明

S_ij表示在a_i结束之后开始，且在a_j开始之前结束的那些活动的集合。而A_ij为S_ij的最大相容子集，且包含活动a_k。由于最优解包含a_k，可以得到两个子问题：
■ 寻找S_ik（a_i结束后开始且在a_k开始前结束）中的最优解；
■ 寻找S_kj（a_k结束后开始且在a_j开始前结束）中的最优解。

又令A_ik = A_ij∩S_ik和A_kj = A_ij∩S_kj。因此，A_ij = A_ik∪{a_k}∪A_kj，|A_ij| = |A_ik| + |A_kj| + 1。

只需证明：A_ij必然包含A_ik和A_kj。
证明过程

• 假设可以找到S_kj相容活动子集A_kj’,满足|A_kj’| > |A_kj|，则可将A_kj’作为S_ij最优解的一部分。这样就可以为S_ij构造出另一个相容活动子集A_ij’，且有|A_ij’| = |A_ik| + |A_kj’| + 1 > |A_ik|+ |A_kj| + 1 = |A_ij| 。这与Aij为Sij的最优解的假设相矛盾。
• 对子问题S_ik类似可证。
  最优子结构得到证明

贪心选择性质的证明

令S_k={a_i∈S: s_i≥f_k}为在ak结束之后开始的活动的集合，Ak为贪心选择ak后的最大相容的活动集合

• 很显然a₁处于原问题最优解中，且可导致原问题的最优解
• 假设当a_k为原问题求解过程的第j个贪心选择且可导致原问题的整体最优解。原问题的最优解由已选择的活动集A_k和子问题S_k的最优解所组成。据贪心选择策略，第j+1次选择S_k中的第一个活动（假设为a_m），显然a_m处于子问题S_k的最优解中，而且可导致原问题的整体最优解。原问题的最优解由已选择的活动集A_m和子问题S_m的最优解所组成。

步骤5：

算法复杂性分析，包括时间复杂性和空间复杂性

• 1. 时间复杂度: O(nlogn)，(b)：O(n) → O(nlogn)
• 2. 空间复杂度: O(n)

步骤6：

算法实现与测试。附上代码或以附件的形式提交，同时贴上算法运行结果截图

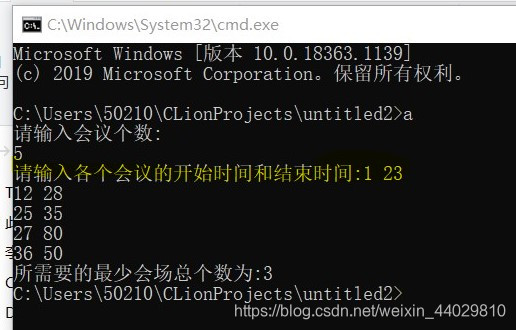
代码运行结果

请输入会议个数:
5
请输入各个会议的开始时间和结束时间:1 23
12 28
25 35
27 80
36 50
所需要的最少会场总个数为:3
进程已结束，退出代码 0

源代码

#include <iostream>class node {
public:int end_time;int flag;int start_time;
};node copy(const node *a, node *b);int comp(int a, int b) { return (a < b) ? 1 : 0; }void quickSort(node *meeting, int low, int high);int main() {int n;std::cin >> n;node *meeting = new node[n];for (int i = 0; i < n; ++i) {std::cin >> meeting[i].start_time >> meeting[i].end_time;meeting[i].flag = 0;}quickSort(meeting, 0, n - 1);//对所有会场按结束时间升序排序int sum = 0;int count = 0;while (n - count > 0) {int cur = 0;for (int i = 0; i < n; ++i) {if (meeting[i].start_time > cur && meeting[i].flag == 0) {meeting[i].flag = 1;cur = meeting[i].end_time;count++;}}sum++;}for (int i = 0; i < n; ++i) {std::cout << meeting[i].start_time << " " << meeting[i].end_time << std::endl;}std::cout << sum;return 0;
}void quickSort(node *meeting, int low, int high) {int key = meeting[low].end_time;int start = low;int end = high;while (end > start) {while (end > start && meeting[end].end_time >= key) {end--;}if (meeting[end].end_time < key) {node temp = meeting[end];meeting[end] = meeting[start];meeting[start] = temp;}while (end > start && meeting[start].end_time <= key)start++;if (meeting[start].end_time > key) {node temp = meeting[start];meeting[start] = meeting[end];meeting[end] = meeting[start];}}if (start > low)quickSort(meeting, low, start - 1);if (end < high) quickSort(meeting, end + 1, high);
}

附上运行结果截图

实验总结

1. 贪心算法的精髓是“今朝有酒今朝醉”。每个阶段的决策一旦做出就不可更改。不允许回溯。

2. 和动态规划的相似之处:
   
   如果大家比较了解动态规划，就会发现它们之间的相似之处。最优解问题大部分都可以拆分成一个个的子问题，把解空间的遍历视作对子问题树的遍历，则以某种形式对树整个的遍历一遍就可以求出最优解，大部分情况下这是不可行的。贪心算法和动态规划本质上是对子问题树的一种修剪，两种算法要求问题都具有的一个性质就是子问题最优性(组成最优解的每一个子问题的解，对于这个子问题本身肯定也是最优的)。动态规划方法代表了这一类问题的一般解法，我们自底向上构造子问题的解，对每一个子树的根，求出下面每一个叶子的值，并且以其中的最优值作为自身的值，其它的值舍弃。而贪心算法是动态规划方法的一个特例，可以证明每一个子树的根的值不取决于下面叶子的值，而只取决于当前问题的状况。换句话说，不需要知道一个节点所有子树的情况，就可以求出这个节点的值。由于贪心算法的这个特性，它对解空间树的遍历不需要自底向上，而只需要自根开始，选择最优的路，一直走到底就可以了。

3. 贪心选择性质:
   
   所求问题的整体最优解可通过一系列局部最优的选择获得，即通过一系列逐步局部最优选择使得最终得到的选择方案是全局最优的。

4. 贪心算法的实现框架

    从问题的某一初始解出发；while （能朝给定总目标前进一步）{利用可行的决策，求出可行解的一个解元素；}由所有解元素组合成问题的一个可行解；

基于分治法的循环日程表算法

问题描述

设有n=2k个运动员要进行羽毛球循环赛，现要设计一个满足以下要求的比赛日程表：

1. 每个选手必须与其它n-1个选手各赛一次；
2. 每个选手一天只能比赛一次；
3. 循环赛一共需要进行n-1天。

采用分治策略求解的分析

  将所有的选手分为两半，n个选手的比赛日程表就可通过为n/2个选手设计的比赛日程表来决定。递归进行分割，直到只剩下2个选手时，比赛日程表的制定就变得很简单。

   假设n位选手被顺序编号为1,2,3,…,n，比赛的日程表是一个n行n-1列的表格，i行j列的表格内容是第i号选手在第j天的比赛对手。当 n 为奇数时，加入一个虚拟队员，其他队员与该队员的比赛视为轮空，则仍可按照前述方法设计日程表。
   按分治策略，可将所有选手对分成为两组，n 个选手的比赛日程表就可以通过为 n/2 个选手设计的比赛日程表来决定。递归地用这种一分为二的策略对选手进行分割，直到只剩下2 个选手。可假设只有8位选手参赛，若1至4号选手之间的比赛日程填在日程表的左上角 (4行3列)，5至8号选手之间的比赛日程填在日程表的左下角(4行3列)；那么左下角的内容可由左上角的对应项加上数字4得到。至此，剩余的右上角(4行4列)是为编号小的1至4号选手与编号大的5至8号选手之间的比赛日程安排。例如，在第4天，让1至4号选 手分别与5至8号选手比赛,以后各天，依次由前一天的日程安排，让5至8号选手“循环 轮转”即可。最后，比赛日程表的右下角的比赛日程表可由，右上角的对应项减去数字4得到。

算法设计

   任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小，越容易直接求解，解题所需的计算时间也越少。
分治法
   分治法是计算机科学中经常使用的一种算法。设计思想是，将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。但是不是所有问题都适合用分治法解决。当求解一个输入规模为n且取值又相当大的问题时，使用蛮力策略效率一般得不到保证。其基本步骤如下：

• (1)分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；
• (2)求解子问题：若子问题规模较小而容易被解决则直接解，否则再继续分解为更小的子问题，直到容易解决；
• (3)合并：将已求解的各个子问题的解，合并为原问题的解。

数据结构

采用二维数组存储比赛信息，i行j列的表格内容是第i号选手在第j天的比赛对手

描述算法

伪代码–递归

ROUND-ROBIN-CALENDAR-REC(A, n) //A[1..n][1..n]IF n==1A[1][1] = 1RETURNROUND-ROBIN-CALENDAR-REC(A, n/2)COPY-CALENDAR(A, n)COPY-CALENDAR(A, n)m = n/2; FOR i = 1 TO m FOR j = 1 TO mA[i][j+m] = A[i][j] + m  //给右上角赋值A[i+m][j] = A[i][j+m]    //右上角抄到左下角A[i+m][j+m] = A[i][j]    //左上角抄到右下角

算法的正确性证明

初始化：如果 n = 1 ( 2^0 = 1 )
则只有一个队伍，自己跟自己打比赛，正确

保持: 先假设函数内部的所有递归调用均满足循环不变式，再证明函数本身返回后，循环不变式仍然成立。每次调用都能保持正确，因为n是2的k次方，每次调用n变成原来的一半，直到最后。

终止：“最外层”的函数调用返回后，算法结果一定是正确的。

算法实现与测试

#include<iostream>
#include<vector>
#include<iterator>
#include<algorithm>
#include<stdio.h>
#include<math.h>
void calender(int **time_table,int n);
void copy_calender(int **time_table,int n);int main()
{int n;int i,j;std::cin >> n;if(n & 1 == 0)n += 1;//如果是奇数，那么就构造成偶数,可有可无（狗头）int **time_table = new int*[n+1];for(i = 0;i <= n-1;i++){time_table[i] = new int[n+1];}//分配空间for(i = 0;i <n/2 ;i++)time_table[0][i]= i+1;//给第一行赋值calender(time_table,n);//分别对右上角，左下角，右下角进行赋值。for(int i = 0; i <= n-1; i++) {for (int j = 0; j <= n-1; j++)std::cout << time_table[i][j] << "|";std::cout << std::endl;}//进行输出return 0;
}
void calender(int **time_table,int n)
{if (1 == n){time_table[0][0] = 1;return;}calender(time_table,n/2);copy_calender(time_table,n);}void copy_calender(int **time_table,int n)
{int m = n/2;for(int i = 0; i < m ; i++)for(int j =0; j < m; j++){//给右上角赋值time_table[i][j+m] = time_table[i][j] + m;//右上角赋值给左下角time_table[i+m][j] = time_table[i][j+m];//左上角赋值给右下角time_table[i+m][j+m] = time_table[i][j];}
}

运行结果

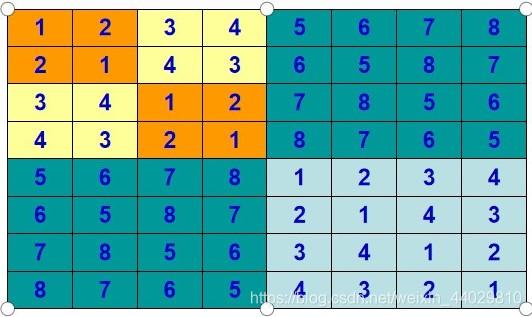
当n=8时

E:\Clion\C++Projects\untitled4\cmake-build-debug\untitled4.exe
8
1|2|3|4|5|6|7|8|
2|1|4|3|6|5|8|7|
3|4|1|2|7|8|5|6|
4|3|2|1|8|7|6|5|
5|6|7|8|1|2|3|4|
6|5|8|7|2|1|4|3|
7|8|5|6|3|4|1|2|
8|7|6|5|4|3|2|1|进程已结束，退出代码 0

当n=4时

E:\Clion\C++Projects\untitled4\cmake-build-debug\untitled4.exe
4
1|2|3|4|
2|1|4|3|
3|4|1|2|
4|3|2|1|进程已结束，退出代码 0

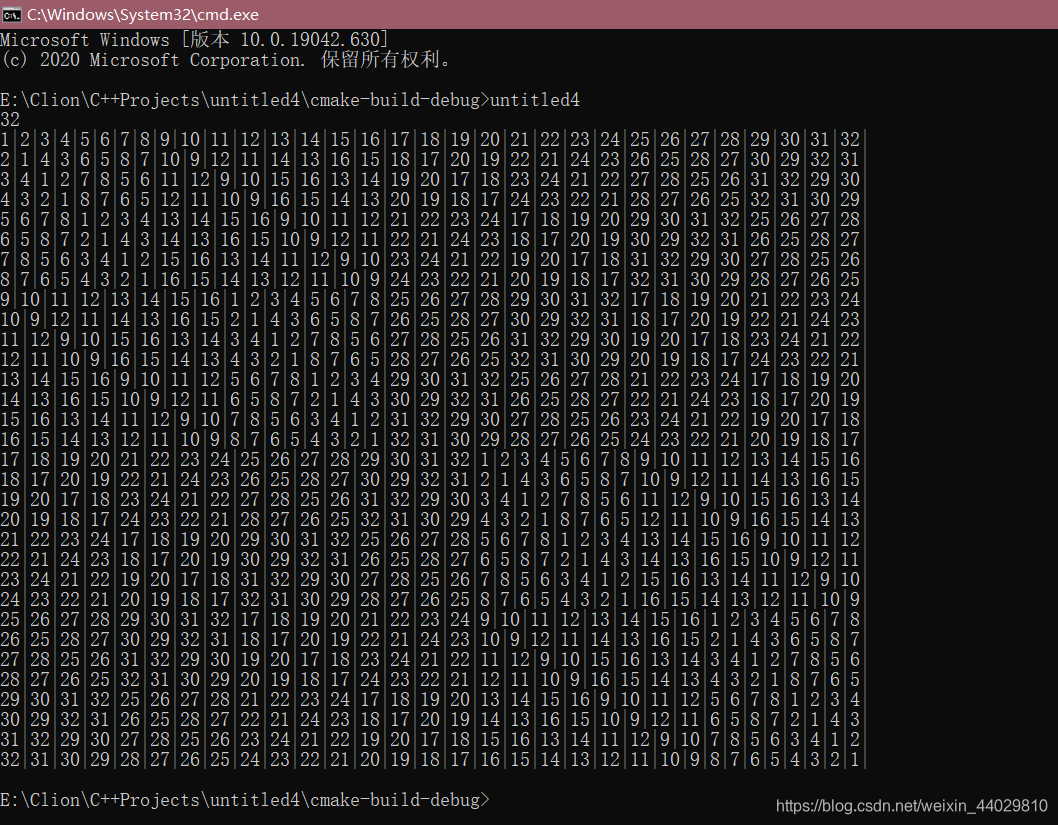
压力测试

实验总结

1.分治算法的基本思想

将一个规模为N的问题，分解成K个规模较小的子问题，这些子问题相互独立且月原问题性质相同。

求解出子问题的解，合并得到原问题的解。

2.分治算法特征分析

分治法能解决的问题一般具有以下几个特征：

1. 该问题的规模缩小到一定程度就可以容易的解决；

2. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；

3. 利用该问题分解出子问题的解，可以合并为该问题的解；

4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题；

分治算法大多采用递归实现，第二条特征就反应了递归思想的引用。

如果满足了第一条特征和第二条特征，不满足第三条特征，可以考虑用贪心法或动态规划法。

如果不满足第四条特征，也可以用分治法，但是要做很多不必要的工作，重复的解公共的子问题，所以一般用动态规划法比较好。

3.实际应用场景

二分查找，阶乘计算，归并排序，堆排序、快速排序、傅里叶变换都用了分治法的思想。

4.依据分治法设计程序的思维过程

实际上类似数学归纳法，找到解决本问题的求解方程公式，然后根据方程公式设计递归程序。

1. 一定是先找到最小问题规模时的求解方法

2. 然后考虑随着问题规模增大时的求解方法

) 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；

3. 利用该问题分解出子问题的解，可以合并为该问题的解；

4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题；

分治算法大多采用递归实现，第二条特征就反应了递归思想的引用。

如果满足了第一条特征和第二条特征，不满足第三条特征，可以考虑用贪心法或动态规划法。

如果不满足第四条特征，也可以用分治法，但是要做很多不必要的工作，重复的解公共的子问题，所以一般用动态规划法比较好。

3.实际应用场景

二分查找，阶乘计算，归并排序，堆排序、快速排序、傅里叶变换都用了分治法的思想。

4.依据分治法设计程序的思维过程

实际上类似数学归纳法，找到解决本问题的求解方程公式，然后根据方程公式设计递归程序。

1. 一定是先找到最小问题规模时的求解方法

2. 然后考虑随着问题规模增大时的求解方法

3. 找到求解的递归函数后，设计递归程序即可。