本文主要是介绍【Literature Notes】Reconstruction of Colored Soft Deformable Objects Based on Self-Generated Template,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
基于自生成模板的彩色柔性可变形物体重建
论文原文:Jituo Li, Xinqi Liu, Haijing Deng, Tianwei Wang, Guodong Lu, and Jin Wang. 2022. Reconstruction of Colored Soft Deformable Objects Based on Self-Generated Template. Comput. Aided Des. 143, C (Feb 2022). https://doi.org/10.1016/j.cad.2021.103124
ABSTRACT
当我们使用RGB-D相机对处在不同变形状态的柔性物体重建时,由于物体自身的遮挡使得捕获的几何形状和纹理信息是不完整的。本篇论文提出一种新的框架,通过一个incremental-completion self-generated template (SGT)解决上述问题,得到具有完整几何形状和一致纹理的可变形柔性物体重建结果。通过构建融合几何形状和光流特征的非刚性配准,SGT能够通过每个初始状态模型所提供的信息进行动态的更新和生成。然后更新后的SGT再反向变形成每种状态,从而获取一系列的动态重建结果。此外,引入马尔科夫随机场来约束网格模型生成一致的纹理和引导非刚性变形。
1 介绍
问题引入:如何真实地模拟柔性物体变形?
解决方法:
- 物理模拟
- 缺点:宏观简化了柔性物体真实的物体特性,很难得到真实的模拟结果。
- 基于data-driven:通过传感器进行柔性物体变形的捕捉和重建,然后将重建结果作为训练数据习得物体的变形规律。
- 优点:更容易探索准确的物理模型,更适合具有复杂变形机制柔性物体的模拟。
随着RGB-D相机(硬件基础)和深度学习技术(软件基础)的发展,第二种方法更具研究价值。
鉴于几何形状的复杂性和光学遮挡,所获的原始数据往往是不完整的,因此不使用基于学习的方法,而采用基于模板的方法。然而,现有的基于先验的模板方法对与具有丰富几何细节的情况创建效率低,所以作者提出一种无需先验即可重建可变形柔性物体的新方法。以下是该方法基于的三个技术:
- 创建自生成模板(SGT)重建柔性物体
- 在SGT和状态模型之间使用一种新的非刚性配准方法
- 基于一致马尔科夫随机场优化生成高质量纹理
2 相关工作
基于RGB-D相机的三维重建:
-
三维静态重建
-
三维动态重建:针对于变形物体重建
- 基于先验
- 不基于先验
-
纹理重建
3 概述

输入到输出整个过程经过四个过程:
- 多状态下服装的3D重建;
- SGT的逐步重建;
- 将SGT拟合到多状态模型;
- 基于一致马尔科夫场优化器生成纹理。
4 SGT的逐步重建
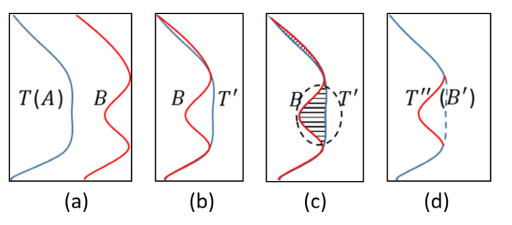
- 使用状态A初始化SGT;
- 将SGT与状态B对齐;
- 在SGT上查找遗失区域;
- 更新SGT。
information missing region (IMR) 的检测和处理:
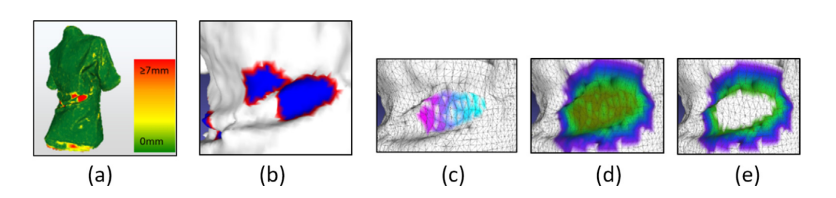
a. 计算SGT上每个点的SSD(surface-surface distances);
b. 基于广度优先算法,通过设定的SSD阈值得到候选的IMRs;
c. 对于IMR最大包围轮廓中出现的一些低于阈值的微小区域,需要合并去除;
d. 将IMR进行膨胀操作实现拓展;
e. 其次,进行腐蚀操作,得到优化后的IMR
5 具有光流特征的非刚性配准
非刚性配准流程:
- 在模板网格中构建图节点(均值分布顶点);
- 计算得到从节点到目标的变换矩阵;
- 计算模板网格中其他点的变形矩阵作为相邻图节点的对偶四元混合矩阵。
为提高鲁棒性,配准过程引入几何和光流特征的约束,通过最小化能量函数实现
E = k 1 E D + k 2 E R + k 3 E 0 E=k_{1} E_{D}+k_{2} E_{R}+k_{3} E_{0} E=k1ED+k2ER+k3E0
- k 1 , k 2 , k 3 k_{1}, k_{2},k_{3} k1,k2,k3:权重系数
- E D E_{D} ED:数据项
- E R E_{R} ER:正则项
- E 0 E_{0} E0:光流特征约束项
5.1. 能量项的定义
E D E_{D} ED 的大小反映了模板网格和目标网格之间的形状差异大小,通过点到平面的误差进行估算。
E D = ∑ i w i φ ( n ^ i ⋅ ( v ^ i − v ˉ i ) ) E_{D}=\sum_{i} w_{i} \varphi\left(\hat{n}_{i} \cdot\left(\hat{v}_{i}-\bar{v}_{i}\right)\right) ED=i∑wiφ(n^i⋅(v^i−vˉi))
Huber惩罚函数:
φ ( x ) = { 1 ∣ x ∣ < δ 2 δ ( ∣ x ∣ − 0.5 δ ) / x 2 other \varphi(x)= \begin{cases}1 & |x|<\delta \\ 2 \delta(|x|-0.5 \delta) / x^{2} & \text { other }\end{cases} φ(x)={12δ(∣x∣−0.5δ)/x2∣x∣<δ other
为使变形平滑变化,使用正则项进行约束:
E R = ∑ i ∑ j , ( i , j ) ∈ E ∥ T i v j − T j v i ∥ 2 E_{R}=\sum_{i} \sum_{j,(i, j) \in E}\left\|T_{i} v_{j}-T_{j} v_{i}\right\|^{2} ER=i∑j,(i,j)∈E∑∥Tivj−Tjvi∥2
光流特征约束项:
E 0 = ∑ i ∥ T i p i − p ˉ i ∥ 2 E_{0}=\sum_{i}\left\|T_{i} p_{i}-\bar{p}_{i}\right\|^{2} E0=i∑∥Tipi−pˉi∥2
光流特征点对,通过光流跟踪搜索对应点,IMR中的点不进行计算,防止引入误差。
将各项计算出来后,得到最小能量函数的最小二乘形式,使用设计的GPU风格的高斯-牛顿求解器进行求解,得到每个节点对应的变换矩阵。
5.2 非刚性变形和SGT的更新
SGT的更新中,SGT中图节点的变换后的点通过对偶四元数插值计算得到。
v ~ i = ∑ j w i , j Q j v i ∑ j w i , j Q j \tilde{v}_{i}=\frac{\sum_{j} w_{i, j} Q_{j} v_{i}}{\sum_{j} w_{i, j} Q_{j}} v~i=∑jwi,jQj∑jwi,jQjvi
v i v_{i} vi是形变前的点, v ~ i \tilde{v}_{i} v~i为形变后的点。
w i , j = exp ( − ∥ v i − p j ∥ / δ j ) w_{i, j}=\exp \left(-\left\|v_{i}-p_{j}\right\| / \delta_{j}\right) wi,j=exp(−∥vi−pj∥/δj)
6 纹理生成
6.1 基于一致马尔可夫随机场的最优视图选择
构建能量函数求解一致马尔可夫随机场优化:
E ( l ) = s 1 E M D a t a ( i , l ) + s 2 E M C o n ( i , l , l i ) + s 3 E M R e g ( i , j , l i , l j ) E(l)=s_{1} E_{M D a t a}(i, l)+s_{2} E_{M C o n}\left(i, l, l^{i}\right)+s_{3} E_{M R e g}\left(i, j, l_{i}, l_{j}\right) E(l)=s1EMData(i,l)+s2EMCon(i,l,li)+s3EMReg(i,j,li,lj)
6.2 基于全局优化的纹理接缝平整
为避免直接拼接纹理贴片造成的明显接缝问题,使用全局优化策略调整每个纹理贴片的颜色,从而平整接缝。
全局优化能量函数:
E ( g ) = ∑ ( f i + g i − f j − g j ) 2 + ∑ ( g k − m − g k − n ) 2 E(g)=\sum\left(f_{i}+g_{i}-f_{j}-g_{j}\right)^{2}+\sum\left(g_{k_{-} m}-g_{k_{-} n}\right)^{2} E(g)=∑(fi+gi−fj−gj)2+∑(gk−m−gk−n)2
实现两个约束:
- 使贴片边缘的纹理差异尽可能小
- 在贴片内部的颜色调整尽可能小
这篇关于【Literature Notes】Reconstruction of Colored Soft Deformable Objects Based on Self-Generated Template的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








