本文主要是介绍(顶刊)多目标优化解决方案集的质量评估:回顾和综述(多目标领域下相当好的一篇文章),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Quality Evaluation of Solution Sets in Multiobjective Optimisation: A Survey
1.摘要
在本文中,提供了解决方案集质量评估的全面回顾。 本文首先介绍了集合质量评价的基本原则和概念,对100个最先进的质量指标进行了总结和分类,重点是这些指标所反映的质量方面。 在每一类别中,都附有对若干具有代表性的指标的详细说明和对其优缺点的深入分析。 此外,还讨论了关于指标所具有的属性和指标所希望具有的属性的问题,希望激励研究人员在设计质量指标时研究这些重要问题,并鼓励从业人员在选择/使用质量指标时铭记这些问题。 最后,提出了该领域的未来趋势和潜在研究方向,以及关于这些方向的一些指导方针。
2.介绍
近20年来文献中对于质量评估指标的研究分成5大类:
- 基于QI(Quality indicator)的设计。 大多数QI研究都属于这一类,旨在设计一个可靠、高效的QI来评估和比较解集
- 基于QI的搜索。 在Zitzler(一个巨佬)和K¨Unzli(2004,基于指标搜索的多目标进化算法:IBEA)的带领下,人们对使用QI来指导多目标优化中的搜索越来越感兴趣。 Jiang等人(2015,一个简单而快速的基于HV超体积指标的多目标进化算法)
- 基于QI的理论研究。 这一类别涉及QI设计中的一些重要问题,包括QIsBretmann和Friedrich(2012年)的计算复杂性分析;Fonseca等人。 (2006年);While等人。 (2012年),并讨论了QI(或QIS的组合)想要的一些属性,如Pare to兼容性和完整性Knowles等。 (2006年)
- 对现有QIS的理解。 这包括对特定QI的行为调查,分析俄歇等人。 (2009年b);Brockhoff等人。 (2012年);Liz´Arraga-Liz´Arraga等人。 (2008年c)或经验性Ishibuchi等人。 (2018b,2015,2014),基准函数Knowles等人对一组QIs的有效性调查。 (2006年);Okabe等人。 (2003年)或在实际应用中,Wang等人。 (2016年),以及不同QIsJiang等人的相关分析。 (2014年);Liefooghe和Derbel(2016年);Ravber等人。 (2017)。
- 回顾QIS的某些方面。 这一类别的工作侧重于从具体角度进行概述,例如审查精确多目标优化器Faulkenberg和Wiecek(2010年)的QIS,对几个已建立的QIS知识(2002年)进行批判性审查;Knowles和Corne(2002年);Okabe等人。 (2003年),对文献中QIs使用频率的统计回顾,Riquelme等人。 (2015年);Wang等人。 (2016年),以及关于如何设计QIS Hansen和Jaszkiewicz的教学评论(1998年);Knowles等人。 (2006年)或如何为特定问题选择合适的QI。 (2018a);Wang等人。 (2016)。
然而,缺少一个这方面的全面回顾,所以本文出现了。
下面是这领域其他方面的综述,读者有兴趣可以去看看。
2011:Multiobjective evolutionary algorithms: A survey of the state of the art
2017:A survey of multiobjective evolutionary algorithms based on decomposition
2015:Many-objective evolutionary algorithms: A survey
2014: A survey of multiobjective evolutionary algorithms for data mining: Part I
2014: A survey of multiobjective evolutionary algorithms for data mining: Part Ⅱ
2014:Benchmarks for dynamic multi-objective optimisation algorithms
3.背景
3.1术语
有兴趣的话也可以参照原文:多目标优化的性能评估:分析与回顾


3.2解决方案的质量
一般来说,解集的质量可以解释为它如何很好地代表帕累托前沿,可以分为四个方面:收敛性、分布性、均匀性和基数性。
收敛性:解集和Pareto前沿的"距离"
分布性:解集覆盖区域
均匀性:顾名思义,解集的均匀程度,均匀性和分布性密切相关,统称为多样性
基数性:解集的基数是指集合中的解数。 一般来说,我们希望有足够的解决方案来清楚地描述集合,但有太多的解决方案可能会让我们不知道用哪个。 然而,人们认为,如果用相同数量的计算资源生成两个集合,则具有更多解的集合是首选的
3.3质量比较
这部分没说啥,就说了可视化分析比较质量不现实,所以我们要用指标。
4.回顾QIs(Quality indicators)
一般来说,QI可分为六类:
- QI用于收敛
- QI用于分布
- QI用于均匀
- QI用于基数
- QI用于分布和均匀性
- QI用于四个质量方面的组合质量。
收敛QIs
收敛QIs是6个中最重要的指标,具体又分成两种:①基于支配关系描述的指标(后图表中1-9)②基于到Pareto前沿的距离(后图表中10-22)
下图是本文精华。
其中,“+”通常意味着该指标能够很好地反映解决方案集的指定质量。 收敛中“-”意味着指标可以在某种程度上反映一组集合的收敛性;例如,指标只考虑支配关系作为收敛度量。 传播中的“-”意味着指标只能反映集合的广度。均匀性的“-”意味着指标可以在某种程度上反映集合的均匀性;也就是说,对等间距集合的干扰不一定会导致更差的评价结果。 基数的“-”意味着在集合中添加一个非主导的解决方案并不一定,但可能会导致更好的评估结果,而且它也永远不会导致更糟糕的评估结果。
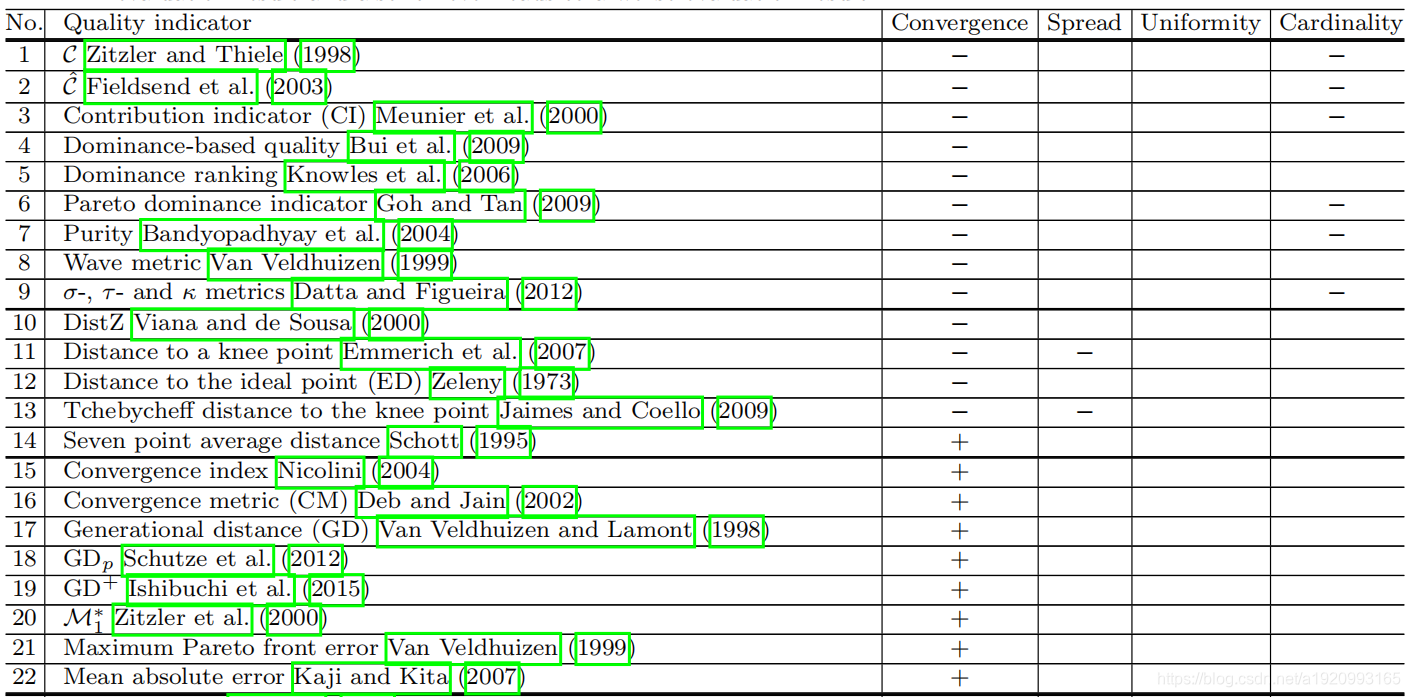
4.1C 指标
C 指标(C Indicator)是描述支配关系的最好的指标。可以描述A,B两个解集的支配关系

C ( A , B ) C(A,B) C(A,B)将 A , B A,B A,B支配关系映射到区间[0,1]。 C ( A , B ) = 0 C(A,B)=0 C(A,B)=0意味着B中的任何一个解都不是由A的任何成员弱支配的, C ( A , B ) = 1 C(A,B)=1 C(A,B)=1意味着A弱支配B。
注意,在两组的质量比较中, C ( A , B ) C(A,B) C(A,B)和 C ( B , A ) C(B,A) C(B,A)都需要考虑,因为C(A,B)不等于1−C(B,A),除非这两组没有相互不支配的解决方案。
4.2GD
(Generational Distance,GD)参考:多目标优化中常用的绩效指标(Performance Indicator)(最全概括)
分布QIs
分布质量与解决方案集覆盖的区域有关。 一个具有良好传播的集合应该包含来自帕累托前沿的每个部分的解决方案,而不遗漏任何区域。(图表中23-33)


4.3MS
MS(Maximum Spread)来自Zitzler等人,是一个广泛使用的分布性指标,它通过考虑每个目标的最大范围来衡量解决方案的范围。 MS被定义为:

其中m表示目标数。在双目标场景中,非支配解集的MS值是其两个极值解的欧氏距离。
然而,正如前面提到的,仅考虑集合的极端解的MS不能反映分布质量。 此外,由于它没有考虑集合的收敛性,远离帕累托前沿的解通常对MS值有很大贡献。 这很容易引起误导性评价。 例如,一个集中在帕累托前沿的一小部分,但有一个离前沿很远的解集将被分配一个好的MS值。
为处理这种情况,有研究者之后进行了改进,详见原文。
均匀QIs
均匀性的质量指标衡量一组解决方案的均匀分布。 由于解集的质量可以看作是它表示Pareto前沿的能力,所以一个均匀分布的解集,它提供了比非均匀的更好的Pareto前沿表示,可以被认为具有更好的质量。(图表中34-44)
值得一提的是,对于集合具有等距解决方案并不能保证具有良好的多样性。 因此,均匀性的QIS应该始终与分布性QI一起使用。
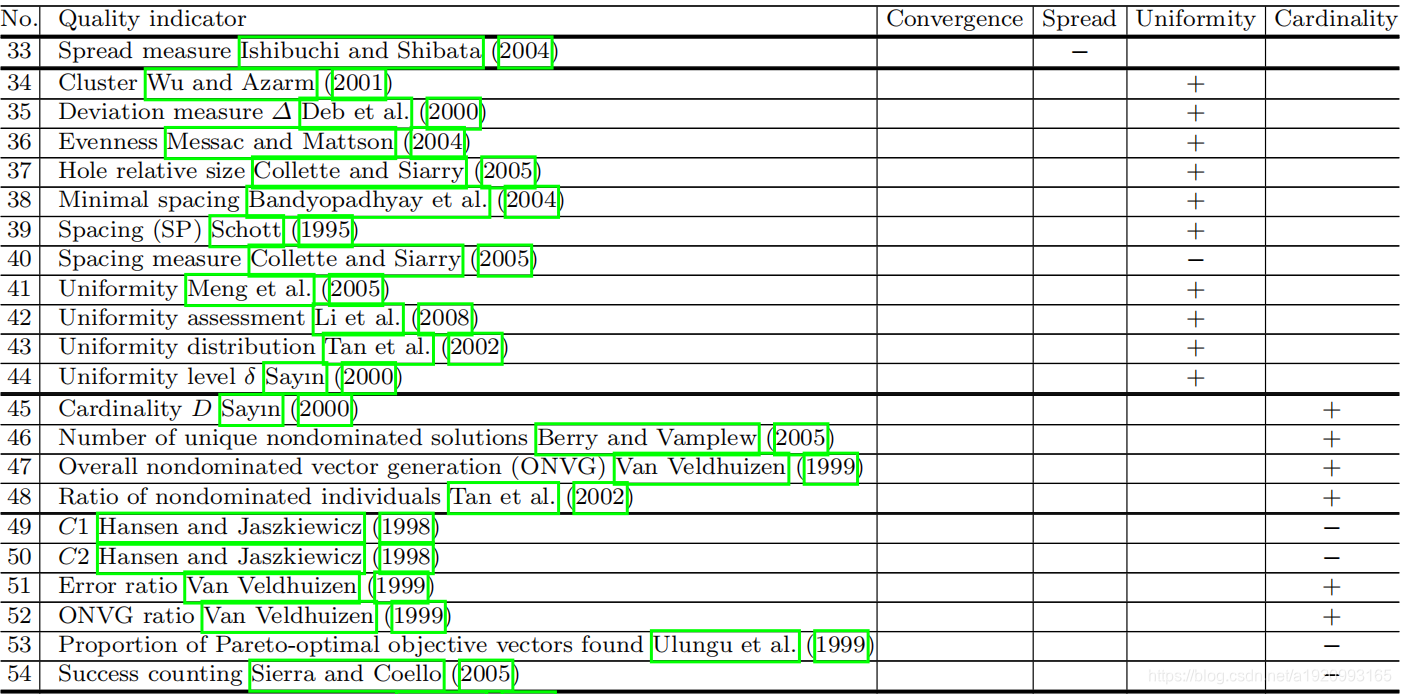
4.4SP
SP(Spacing)是最受欢迎的分布性指标。具体地,给出 A = a 1 , a 2 , . . . , a N A = {a1, a2, ..., aN} A=a1,a2,...,aN,有:

其中d是所有d1(a1,A/a1)、d1(a2,A/a2)、、d1(a N,A/aN)和d1(ai,A/ai)的平均值,即ai与集合A/ai的L1范数距离

其中m表示目标数,aij是解ai的第j个目标。 SP值越低,均匀性越好。
基数QIs
基数的QIS可以归结为一个简单的想法-计算非主导解的数量。
根据帕累托最优解的参与,基于基数的QIS可以分为两类。 一种是直接考虑集合中的非主导解决方案,即非支配解数或非支配解的比例(图表中45-48)。另一种比较了解集合中的非主解和问题的帕累托最优解(图表中49-54)。
4.5ER
ER(Error Ratio)指标由Van Veldhuizen于1999年提出,考虑了解集非支配解的比例,即帕累托最优解。具体:

其中N是集合A的大小,并且:

ER越小越好。ER值为0表明,所考虑的集合中的每个解都是问题的帕累托最优解。
分布和均匀的QIs
如前所述,分布和均匀性的质量方面是密切相关的,它们需要一起考虑,以反映解决方案集的多样性。 这激励QIS既涵盖传播质量,也涵盖均匀性质量。 这一类别中的大多数QI可以分为两类,即基于距离的指标和基于区域划分的指标,尽管存在替代品,如基于集群的指标Li等。 (2005年);Meunier等人。 (2000年)和基于数量的指标Jiang等人。 (2016年);Tian等人。 (2019)。 (图表中55-74)。
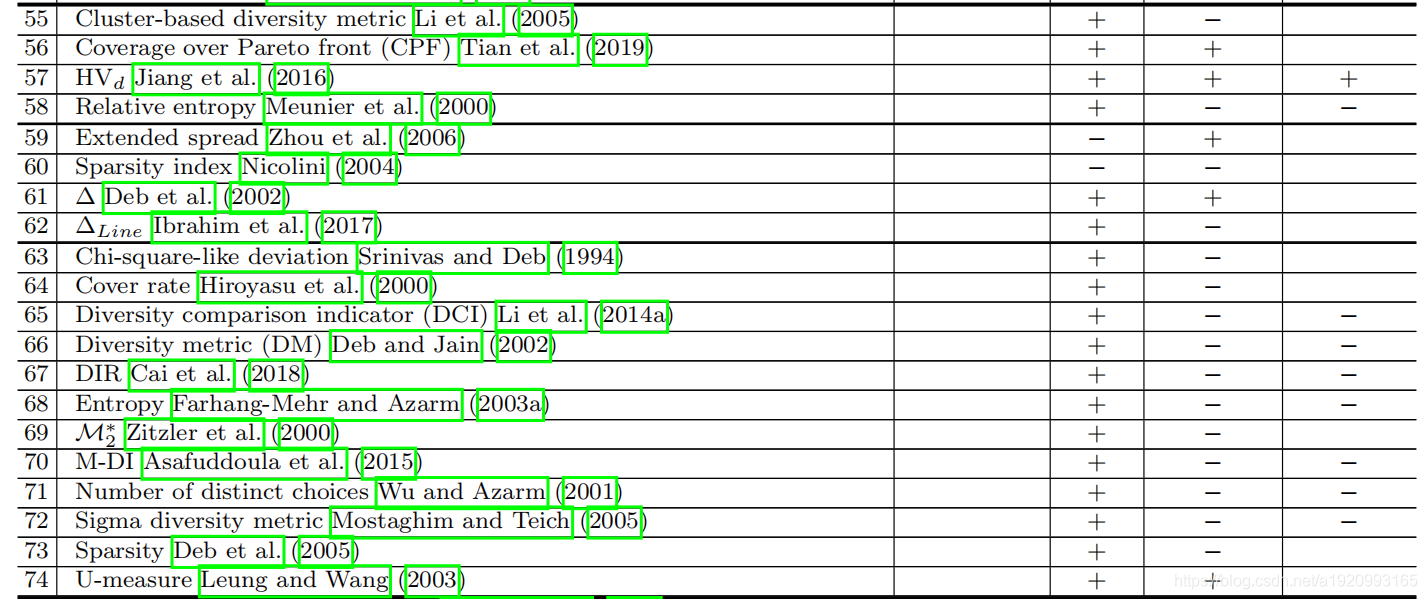
4.6基于距离的QIS
该类中的QIS通常考虑解决方案与其邻居之间的距离,然后总结这些距离,以便估计整个集合的覆盖范围(图表中59-62)。然而,这种评价只能在双目标问题中工作,因为非支配解是连续地位于两个目标上的。 这些QIS的另一个问题是,它们需要帕累托前沿的信息(例如边界)作为参考,这在实践中往往是未知的。
4.7基于区域划分的QIS
这个类的基本思想(图表中63-74)是将一个特定的空间划分为许多大小相等的单元格(有重叠或没有重叠),然后计算具有集合解的单元格的数量。 这是基于这样一个事实,即一组更多样化的解决方案通常占据更多的单元。 大多数用于扩展和均匀性的QIS都属于这一类,考虑到小区域的不同形状。
4.8多样性比较指标DCI
Diversity Comparison Indicator(DCI),这一类别中的质量指标可能不是很实用,特别是在高维场景中。 在基于距离的QIS中,需要问题的Pare to前沿的信息,而在基于区域划分的QIS中,考虑的单元数通常随目标维数呈指数增长。
DCI评估几个解决方案集之间的相对质量。为此,首先将考虑的所有集放入网格中,这样就有一些框有一个或几个解决方案。DCI考虑了所有集合组合集合的非主导解的位置。然后对于每个盒子,DCI计算每个集合的贡献度。贡献度是一个值∈[0,1],随着从集合到盒子的距离的增加而单调减小。一个值意味着盒子中至少存在一个解决方案,零意味着盒子的邻域中没有解决方案,其中邻域大小与目标数一致增加。 最后,DCI将集合对所有考虑框的贡献度作为其评估结果。 它将n个分数(在[0,1]范围内)分配给n个解集。 如果一组的解决方案覆盖或接近所有框,并且如果它的解决方案远离大多数框,则将获得高分。 然而,值得注意的是,由于所考虑的框通常不是均匀分布的,DCI可能更喜欢与其他框具有相似分布的集合。
所有质量方面的QI
这一类别的质量指标在文献中最常用,因为它们涵盖了解决方案集质量的所有四个方面。 (图表中75-100)。
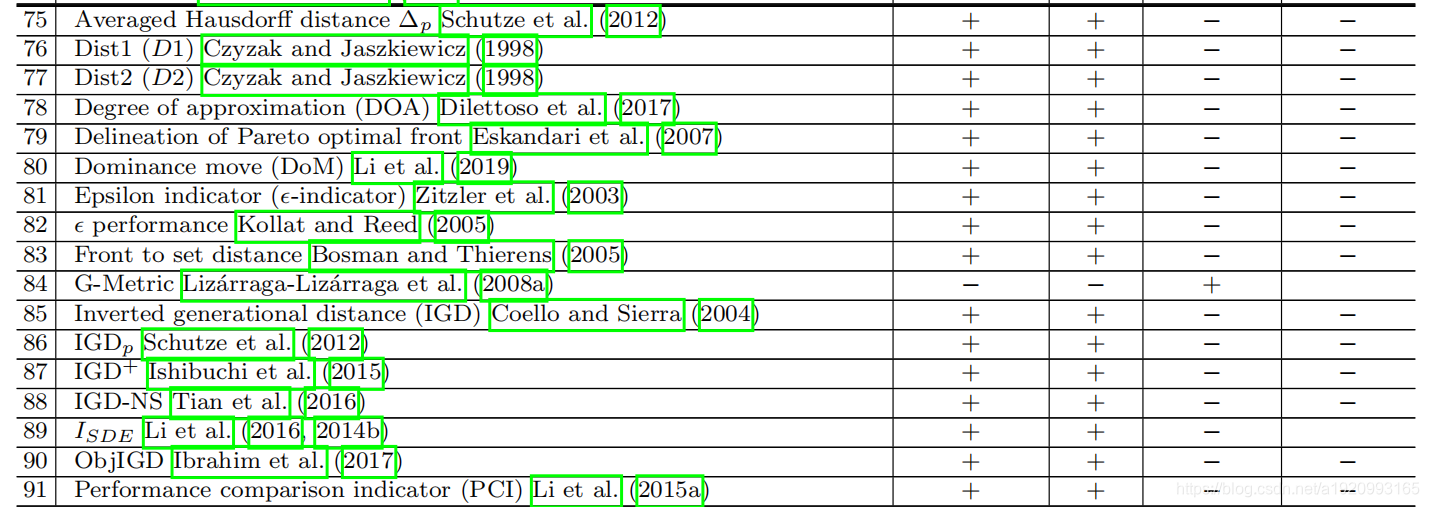
一般来说,它们可以分为两类:基于距离的QIS(图表中75-91)和基于体积的QIS(图表中92-100)。
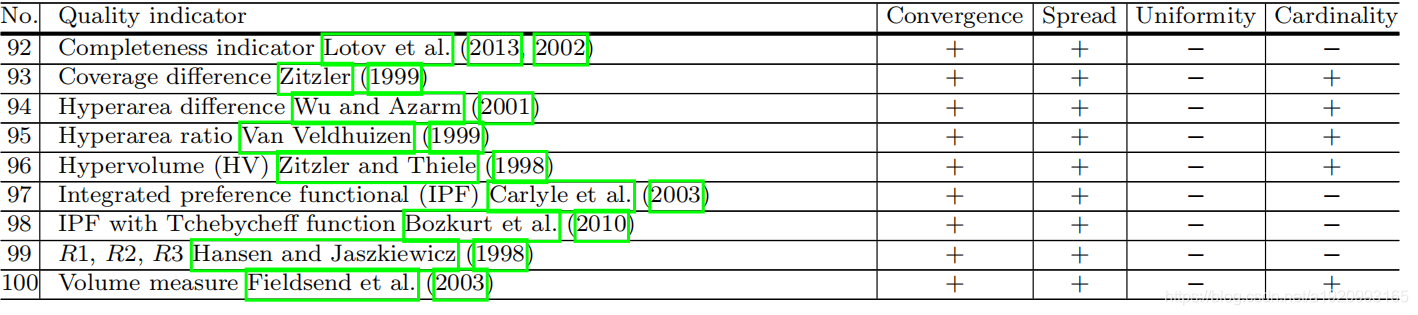
4.9基于距离的QIS
基于距离的QIS的基本思想是测量帕累托前沿到所考虑的解集的距离。 因此,需要一个很好地代表帕累托前沿的参考集。 只有接近参考集的每个成员的解集才能具有良好的评价价值,从而反映了所有质量方面的收敛性、传播性、均匀性和基数性。
代表的有IGD,DOM等。
4.10基于体积的QI
该类中的QIS(图表中92-100)测量由考虑的解决方案集与某些规范一起确定的体积的大小。 其中,广泛使用的指示器超体积(hypervolume,HV)由Zitzler和Thiele在1998年提出的,计算由集合和用户指定的参考点所包围的区域的体积。
之后,HV的计算得到了修改和扩展,1999年Multiobjective evolutionary algorithms: Classifications, analyses, and new innovations 中提出 hyperarea ratio;2003年Metrics for quality assessment of a multiobjective design optimization solutionset 中提出 hyperarea difference;1999年Evolutionary Algorithms for Multiobjective Optimization: Methods and Applications 中提出coverage difference等等
最后,值得注意的是,如最后的图所示,没有QI能够很好地反映所有四个质量方面。 这并不奇怪,因为质量方面可能在某种程度上相互冲突,例如趋同与统一。 例如,考虑一组均匀分布的解。 我们可以在集合中稍微移动一个解,使它具有更好的收敛性。 这将导致一个新的集合具有更好的收敛性,但更差的均匀性。 显然,在这个例子中,单个QI不可能捕捉到两个质量方面。 另一方面,从表中可以看出,只有HV(及其变体,图表中93-96和100)能够很好地反映质量基数。 这是因为HV是唯一已知的与“更好”关系完全一致的指标,因此它对集合中非支配解的任何变化都很敏感。
4.11 I G D IGD IGD
Inverted Generational Distance,IGD参考多目标优化中常用的绩效指标(Performance Indicator)(最全概括)
4.12 ϵ − i n d i c a t o r \epsilon-indicator ϵ−indicator
与IGD不同, ϵ − 指 标 \epsilon-指标 ϵ−指标由Zitzler等人于2003年提出,考虑了解集之间的最大差异。
给定两个解集, ϵ − 指 标 \epsilon-指标 ϵ−指标是一个集合必须在目标中转换(以加法或乘法的方式)以弱支配另一个集合的最小因子。 这导致了两个版本:加法 ϵ − 指 标 \epsilon-指标 ϵ−指标和乘法 ϵ − 指 标 \epsilon-指标 ϵ−指标。 从数学上讲,集合A到集合B的加法 ϵ − 指 标 \epsilon-指标 ϵ−指标被定义为:

其中aj表示a的第j个目标,m是目标数。
集合A到集合B的乘法 ϵ − 指 标 \epsilon-指标 ϵ−指标被定义为:

这两个指标都越小越好。 ϵ + \epsilon+ ϵ+(A,B)≤0或 ϵ ∗ \epsilon* ϵ∗(A,B)≤1的值意味着A弱支配B。 当用表示帕累托前沿的参考集R代替B时, ϵ − 指 标 \epsilon-指标 ϵ−指标可以作为一元指标。 它测量考虑到的集合到帕累托前沿的差距。。然而,由于返回的值只涉及任何一组中一个特定解决方案的一个特定目标(其中最大差异是),因此该指标可能省略大量集合的差异。
4.13HV
Hypervolume,HV由Zitzler和Thiele(1998年)最初被作为所覆盖空间的大小提出,原文为Multiobjective optimization using evolutionary algorithms - A comparative case study.
HV可以说是最常用的QIS,因为它具有理想的实际可用性和理论特性。 计算HV不需要表示帕累托前沿的参考集,这使得它适合于许多现实世界的优化场景。HV的结果对于任何相对于帕累托优势改进的集合是敏感的。当集合A优于另一组B时,HV返回A的质量值高于B。因此,对于给定问题,实现最大HV值的集合将包含所有Pare to最优解。
HV可以定义如下。 给定解集A和参考点r,HV可以计算为:

其中λ表示Lebesgue测度。 简单地说,集合的HV值可以看作是由其每个解和参考点(分别作为左底顶点和右顶顶点)确定的超立方体的结合的体积)。
HV的一个限制是它在目标数方面的指数增长运行时,即耗时。另外,HV的另一个问题是其参考点的设置。 尽管有一些常见的做法,例如帕累托前沿的最低点或比较解集集合的最低点的1.1倍,但对于如何为给定的问题选择适当的参考点仍然没有共识。不同的参考点会导致HV评估结果不一致,Knowles和Corne(2003)。最近,Ishibuchi等人(2017年,2018年)在指定单纯形Pare to前沿和倒置单纯形Pare to前沿问题的适当参考点方面表现出明显的差异。 它们还在实验上表明,比最低点稍差的参考点并不总是合适的,特别是对于多目标优化和/或人口规模较小的情况。此外,HV指示器更偏向于凸区域而不是凹区域Zitzler和Thiele(1998)。 正如Auger等人所证明的那样。 (2009b),一组达到最大HV值的解的分布在很大程度上取决于帕累托前沿的斜率。 例如,HV可能有利于高度非线性帕累托前沿的非常不均匀的解集。 这在Li等人中已经得到了证明。 (2015a)。
4.14IPF
Integrated Preference Functional,IPF,略
4.15R Family
略
5.质量评价的重要问题
5.1一元,二元,多元指标
QIs处理的解决方案集的数量可能不同。 虽然大多数QI都是一元指标,通过给它分配一个实数来独立地评价一个解集,但也存在一些M-元指标(M>2),它们通过通常分配M实数来给出M解集的相对质量。 例如,R家族Hansen和Jaszkiewicz(1998年)和C指标Zitzler和Thiele(1998年)是最早的二进制QI,其次是-指标Zitzler等人。 (2003年),而G-计量Liz´Arraga-Liz等人。 (2008a),DCI Li等人。 (2014a)和PCILi等人。 (2015a)旨在一次比较任意数量的集合。 与一元QI相比,M-NaryQIs具有一些优点,例如所需的参考信息较少(因为所考虑的集合可以相互引用),并且更容易符合Pare to优势(如果在评估中引入对集合之间优势关系的比较)。
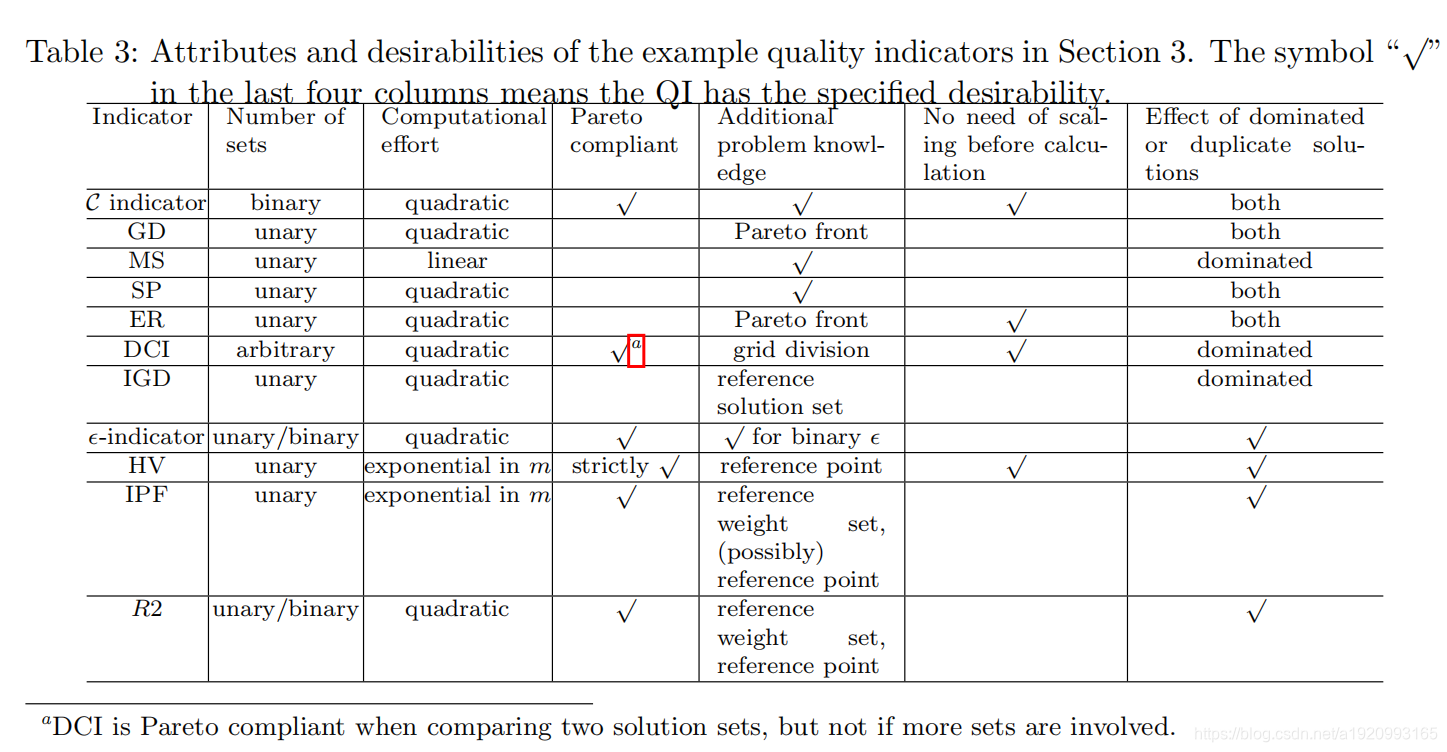
5.2计算成本
大多数QIS计算起来代价很小。 基数QIs和多样性QIs(即评估分布和/或均匀性)的时间复杂度在解集的大小上分别是线性和二次的。 涉及参考解决方案/权重集的QI通常需要O(mNR)比较,例如GD、IGD和R2指标,其中m表示目标数,N表示解决方案集的大小,R表示参考集的大小;因此,在参考集的合理大小下,不需要担心这些QI的运行时间。对于M-NaryQI,通常需要 O ( m N 2 M ) O(mN^2M) O(mN2M)比较,因为它们需要将一组中的每个解决方案与其他组的所有解决方案进行比较,例如C、DCI和 ϵ − \epsilon- ϵ−指标。 HV、IPF及其变体是昂贵的QIS之一,它们的计算时间随着目标的数量呈指数增长。 这可能会限制它们在高维空间中的应用,特别是作为集成到优化器搜索过程中的指示器。 最昂贵的QI是DoM,其计算时间随解集的大小呈指数增长。
HV的计算在过去15年中受到了广泛的关注。 这个问题被证明是Klee测量问题(Beume,2009)的一个特例。 对于二维和三维情况,最优计算时间为O(NlogN),这由Beume等人于2009证明。其中,最著名的算法实现了 O ( N m / 3 p o l y l o g N ) O(N^{m/3}polylogN) O(Nm/3polylogN)上界(Klee’s measure problem made easy,Chan,2013),其中N表示集合的大小,m表示目标数。但当用作指导搜索的指示器时,仍然很困难。
虽然用蒙特卡罗抽样近似HV可以显著减少其计算时间(An algorithm for fast hypervolume-based many-objective optimization,Bader和Zitzler,2011);Bretmann等人(2013年);Ishibuchi等人(2010年),它仍然面临“维度诅咒”的问题,当目标数量达到20个时,它可能无法区分不同的解决方案集。
5.3附加问题知识
大多数QIS需要额外的问题信息,特别是与收敛相关的QIS,它们通常需要问题的帕累托前沿的某种引用来进行比较,例如理想点、最低点或表示前沿的引用集。 由于QIS的准确性在很大程度上取决于这些引用,因此QIS最好尽可能少地获得参考信息。 在报告研究结果时,强烈建议将评估值与所使用的参考信息相伴随,例如,明确注意所使用的参考点或使所使用的参考集公开,以便其他人可以站在同一页上比较他们的结果。
5.4参考点
在QIS中经常使用的参考点是理想点和最低点(或由它们导出的参考点)。 例如,基于Tchebycheff实用程序函数的IPF和R2需要问题的理想点,HV指示器需要一个参考点,该参考点通常是从最低点导出的。 虽然问题的真正理想点通常是不可用的,但我们可以使用由正在考虑的解集获得的估计点,或者通过单独优化问题的每个目标。请注意,不要低估理想点是至关重要的,因为这可能导致与估计的理想点不占优势的解决方案,而不是对评价结果作出充分贡献。 此外,即使使用了精确的理想点,边界解的贡献仍然可能小于内部解,如IPF和R2。
5.5参考集
在许多QI中需要一个表示帕累托前部的参考集,如IGD、一元 ϵ − \epsilon- ϵ−指标和相对的HV(即超面积比,范维尔德韦森(1999))。理想情况下,这样的参考集预计将由均匀而密集地分布在帕累托前面的足够点组成。但在大多数情况下,这是不可行的。一个实际的替代方法是使用所考虑的解决方案集的集合作为参考集。然而,这种常见的做法可能有两个问题。首先,当比较中包含新的解决方案集时,需要重建参考集。更重要的是,这样的集合可能不能很好地表示帕累托前面,因此QI可能返回不准确的结果。
一方面,参考集可能使QIS更喜欢与大多数考虑的解集一致的特定分布模式。 这意味着,如果一个解决方案集与其他解决方案集的分布非常不同,那么无论它的实际分布如何,这个集合都可能分配一个较差的评估值。 这特别适用于对参考集分布敏感的QI,如 I G D IGD IGD和 I G D + IGD^{+} IGD+。下图给了个很好的例子。当将A与B进行比较时,如果参考集由这两个集合组成,我们将得到比B更好的(IGD(A)≈1.41<IGD(B)≈2.12)。 但是,如果在评估中添加另一个具有与B相似分布模式的集合C,并且现在参考集由这三个集合组成,我们将有比B更差的A(IGD(A)≈1.82>IGD(B)≈1.72)。

5.6缩放和正则化
略
5.7添加支配解或重复解的效果
有些指标添加支配解或重复解后会发生变化,但有些不会s,比如 H V , I G D + , I P F , P C I , R 2 , 和 ϵ − i n d i c a t o r HV, IGD^{+}, IPF, PCI, R2, 和\epsilon-indicator HV,IGD+,IPF,PCI,R2,和ϵ−indicator.
6.未来工作
有四方面工作这里略过:
- QI的设计
- QI的选择
- QI之间的联系
- 最优分配量
6.1基于指标的搜索
多目标优化的一个趋势是将QIs集成到优化器本身中。 由于优化器的结果最终由QIs评估,在搜索过程中直接优化QI值是自然和合乎逻辑的,从而导致在集合空间而不是在解决方案空间中进行搜索。 这种基于指标的搜索,以及基于帕累托的搜索和基于分解的搜索,已经成为进化多目标优化的三种主流技术。
下图是基于指标的优化方法,有兴趣可以去原文。
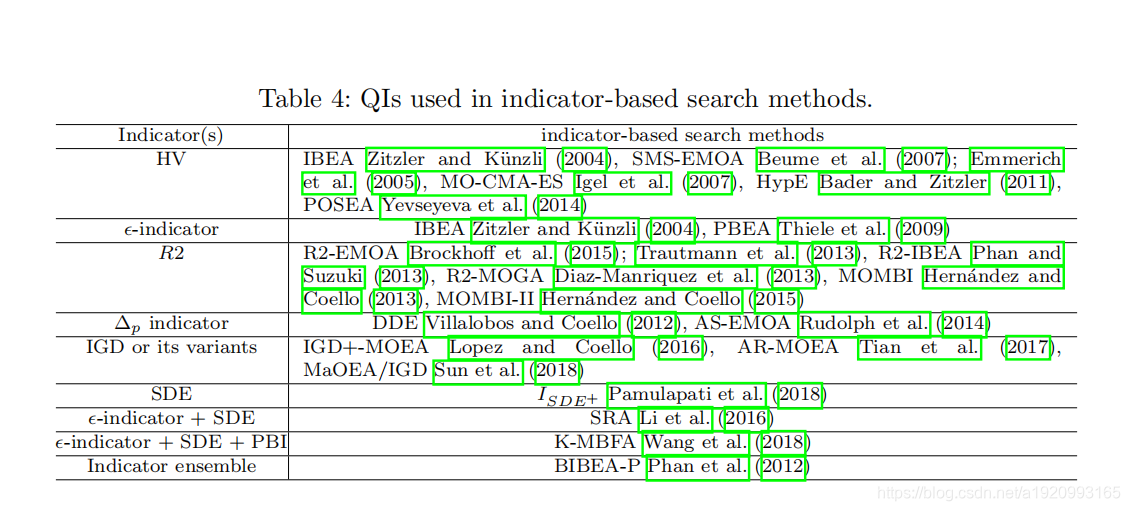
这些方法被发现在有许多目标(many objectives)的问题中特别有希望,因为它们可以提供足够的选择压力(相对于帕累托优势),为具有任何维度的解集返回标量值。
然而,与基于解决方案的选择相比,这种基于集合的选择通常伴随着较高的计算成本。 每次我们删除集合中的一个解决方案时,它可能需要N个评估来确定哪个对指标的贡献最少。 基于指标的优化器的另一个问题是,它们当然依赖于被考虑的QI的准确性和行为。 由于每个指标代表一个特定的偏好结构,似乎有希望将一个指标与一般的帕累托优势关系相结合,或者考虑具有不同偏好结构的多个指标。
6.2HV相关问题
HV指示器长期以来一直是进化多目标优化领域的中心主题之一。 在基于HV的搜索中存在着计算复杂度、增量更新和子集选择等几个不断引起研究者关注的开放问题。 感兴趣的读者可参阅以下两个网页,http://simco.gforge. inria.fr/doku.php?id=openblems和http://www.hypervolume.org.
6.2.1时间复杂度
略
6.2.2增量更新
增量更新HV(也称为计算HV贡献)是测量当一个解决方案被添加到或从集合中移除时,集合的HV值变化了多少。它在基于HV的档案维护中起着重要的作用。 (Bounded archiving using the Lebesgue measure,2003)和基于HV的进化搜索 (On the Complexity of Computing the Hypervolume Indicator,2005)。
原文这里提到其他的一些针对该问题的算法,有兴趣的话。
6.3从用户的角度理解
QIS的另一个问题是评估结果对用户的可理解性。 基于QI评估解决方案集返回的一个或多个标量值,用户可能很难理解解决方案集的质量,特别是对于那些在多目标优化方面没有专门知识的人来说。
7.总结
在现实生活中,多目标优化器被应用的问题是普遍存在的,这表明需要仔细分析和公平评估优化器的结果。 本文对多目标优化中的质量评价进行了全面的综述。 我们对100个质量指标进行了分类,详细介绍了几个有代表性的指标,并讨论了质量指标所具有或希望具有的一些性质。 所有这些都意味着一个结论,即没有理想的质量指标来评估解决方案集和适合不同情况的不同指标。例如,HV由于其对优势地位改善的敏感性,可以是一个很好的选择,当问题的最低点可以很好地估计,例如在大多数基准情景中。 R2适用于各种双目标场景,我们建议使用比理想点稍好一点的参考点。 ϵ − \epsilon- ϵ−指标是现实世界场景的一种选择,因为它不受参考集的分布和位置的影响。 需要分别用GD和IGD代替GD和IGD。 与高压相比,后者可以用于具有高目标维数和/或大集大小的基准场景,只要有密集和均匀分布的参考集。
下图是个简单总结:
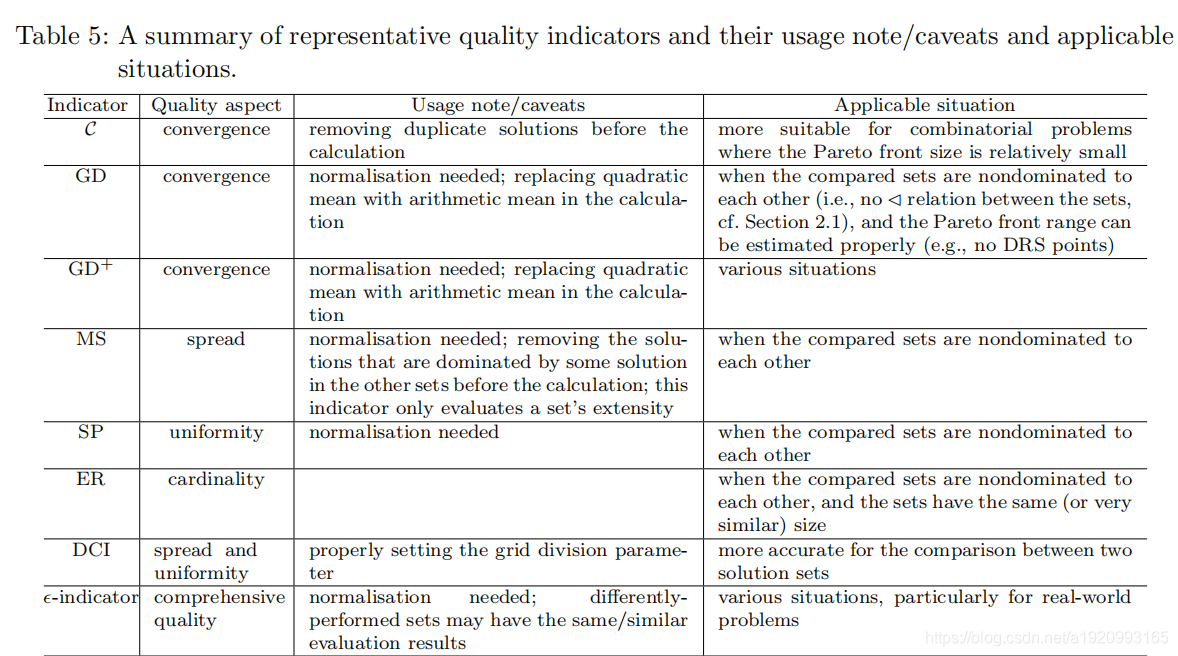

返回受约束的多目标优化问题优秀论文及总结目录
这篇关于(顶刊)多目标优化解决方案集的质量评估:回顾和综述(多目标领域下相当好的一篇文章)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


