本文主要是介绍场效应晶体管及其放大电路,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
场效应管
- MOS场效应管
- 增强型场效应管
- 增强型NMOS输出特性曲线
- 增强型NMOS管转移特性曲线
- MOS场效应管衬底调制效应
- PMOS场效应管
- 耗尽型场效应管
- 结型场效应管
- 场效应管的放大电路
- 场效应管直流偏置电路
MOS场效应管
增强型场效应管
- N沟道增强型MOS管的结构
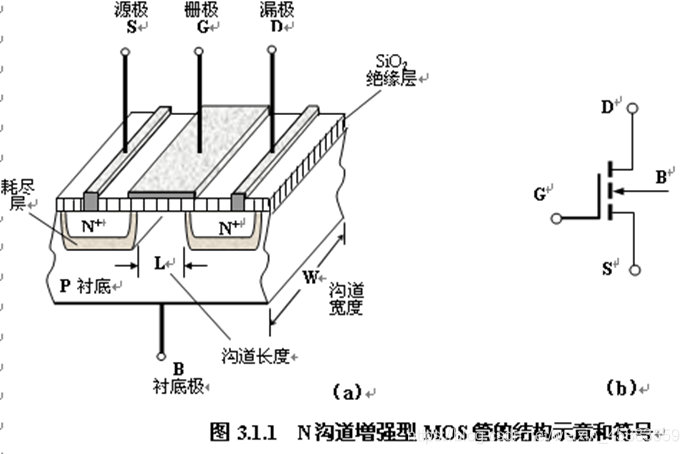
- 基本工作原理:
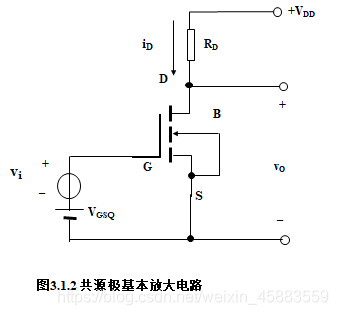
与晶体管不同的是, NMOS管多了一个衬底B, 在场效应管正常应用时, 漏极D, 源极S与衬底B之间的PN结不应该出现正向导通的情况, 这要求衬源电压 v B S ≤ 0 v_{BS}\leq0 vBS≤0. 单个增强型NMOS管构成放大电路时, 可将衬底和源极短接, 即令 v B S = 0 v_{BS}=0 vBS=0. 如上图由但NMOS管构成的共源极基本放大电路, 衬底应该接电位最低点, 以保证所有MOS管的PN结都反偏.- 栅源电压 v G S v_{GS} vGS对MOS管沟道的影响.
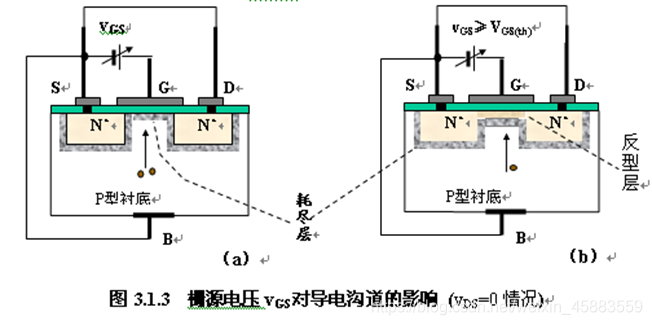
令 v D S = 0 v_{DS}=0 vDS=0, 将源极和衬底直接相连, 在源极, 栅极之间加有电压 v G S > 0 v_{GS}>0 vGS>0时, 栅极与源极, 栅极与漏极, 栅极与衬底之间形成了电场, 使得P型衬底中的自由电子向栅极方向运动, 与绝缘层下方的空穴复合, 使栅极下方出现了一层耗尽层. 当 v G S v_{GS} vGS再增加时, 更多电子到达栅极下方, 超过空穴浓度, 使得该区域的半导体由P型转换成N型, 称这个区域的半导体为反型层.反型层作为导电沟道将漏区, 源区连通. 进一步增加 v G S v_{GS} vGS, 反型层的厚度会增加.
刚刚出现反型层使得栅源电压 v G S v_{GS} vGS称为MOS管的开启电压, 用 V G S ( t h ) V_{GS(th)} VGS(th)表示, 简写为 V t h V_{th} Vth. 其由NMOS管的工艺, 材料决定. - 漏源电压 v D S v_{DS} vDS对MOS管沟道得影响
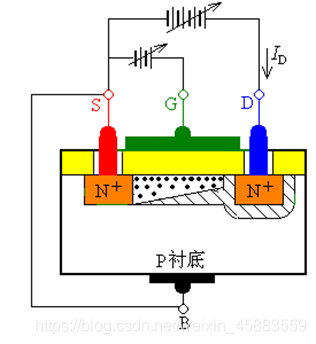
当 v G S < V t h v_{GS}<V_{th} vGS<Vth时, 漏区, 源区之间没有沟道形成, 漏源之间是NPN结构, 相当于有两个PN结, 在漏极和源极之间加电压 v D S v_{DS} vDS时, 总有一个PN结反向偏置, 因此漏源电流基本为0, 此状态称为MOS管的截止状态, 场效应管工作在截止区.
如果 v G S > V t h v_{GS}>V_{th} vGS>Vth, 使导电沟道形成后, 在漏源极之间加电压 v D S v_{DS} vDS, 当 v D S v_{DS} vDS有0正向增大时, 漏栅极间电压小于栅源极间电压, 即 v G S − v D S = v G D < v G S v_{GS}-v_{DS}=v_{GD}<v_{GS} vGS−vDS=vGD<vGS, 使得沟道靠近漏极一侧吸引自由电子数量小于源极一侧, 靠近漏极得导电沟道将变得相对较薄. 此时场效应管工作在可变电阻区.
当 v D S v_{DS} vDS增大到恰使栅漏极间电压 v G D v_{GD} vGD等于开启电压 V t h V_{th} Vth, 靠近漏区得一侧反型层完全消失, 退为耗尽层, 即导电沟道在该位置点被夹断, 称此状态为预夹断. 此时, v G S − v D S = V t h v_{GS}-v_{DS}=V_{th} vGS−vDS=Vth.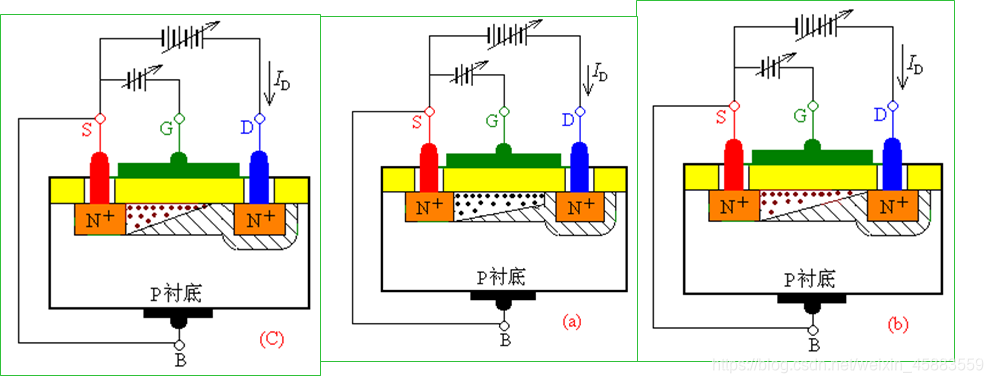
在预夹断产生后继续增大 v D S v_{DS} vDS, 使得 v G D < V t h v_{GD}<V_{th} vGD<Vth, 加断点向源区方向移动, 靠近漏区一侧得导电沟道被耗尽层夹断的部分增多, 沟道长度变短. 载 v D S v_{DS} vDS得作用下, 在夹断点与漏极之间的耗尽层上产生了较强的电场, 自由电子由源取沿导电沟道向漏区方向运动并达到夹断点, 被耗尽区内的强电场作用继续向漏区漂移, 依然形成漏极电流 i D i_D iD, 且 i D i_D iD基本不随 v D S v_{DS} vDS的增加而增加, 此时场效应管工作在饱和区(或称为恒流区)
- 栅源电压 v G S v_{GS} vGS对MOS管沟道的影响.
增强型NMOS输出特性曲线
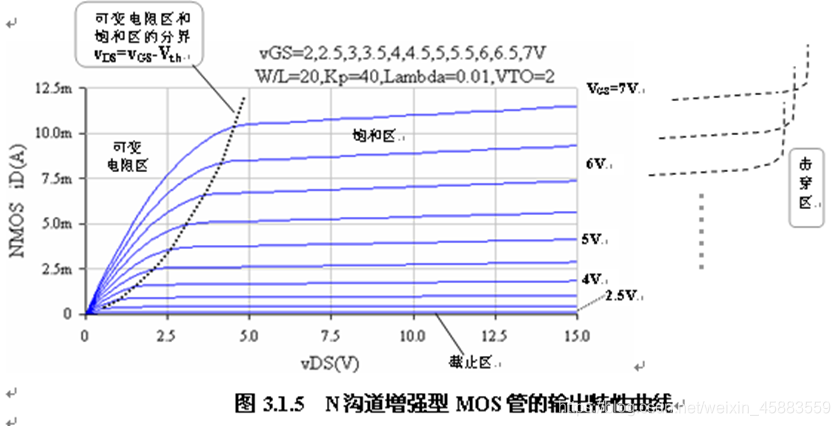
根据 i D i_D iD和 v G S , v D S v_{GS},v_{DS} vGS,vDS的关系特点, 可在输出特性曲线上分为4个区域: 截止区, 饱和区, 可变电阻区和击穿区.
- 截止区: v G S < V t h v_{GS}<V_{th} vGS<Vth, 导电沟道未形成, 漏, 源极电流 i D i_{D} iD很小, 漏源极间呈现很大电阻. 一般认为 i D = 0 i_D=0 iD=0, 漏源极呈断开状态. 研究表明, 当 v G S v_{GS} vGS接近 V t h V_{th} Vth时, 电流 i D i_D iD并不无限接近于0, 一般可在 μ A \mu A μA数量级且 i D i_{D} iD与 v G S v_{GS} vGS呈指数关系. 这种现象称为亚阈区效应. 在后面的分析中, 不考虑亚阈区效应.
- 可变电阻区: v G S > V t h , v D S < v G S − V t h , v G D > V t h v_{GS}>V_{th}, v_{DS}<v_{GS}-V_{th}, v_{GD}>V_{th} vGS>Vth,vDS<vGS−Vth,vGD>Vth. 漏源极间存在未被夹断的导电沟道. 漏极电流 i D i_D iD随 v D S v_{DS} vDS增大而增大, i D , v D S , v G S i_{D},v_{DS},v_{GS} iD,vDS,vGS间的关系可表示为 i D = k p 2 ⋅ W L [ 2 ( v G S − V t h ) v D S − v D S 2 ] − − − v G S > V t h , 0 < v D S < v G S − V t h i_D=\frac{k_p}{2}\cdot \frac{W}{L}[2(v_{GS}-V_{th})v_{DS}-v_{DS}^2]---v_{GS}>V_{th}, 0<v_{DS}<v_{GS}-V_{th} iD=2kp⋅LW[2(vGS−Vth)vDS−vDS2]−−−vGS>Vth,0<vDS<vGS−Vth式中 k p = μ n C o x k_p=\mu_n C_{ox} kp=μnCox称为本征导电因子 ( A / V 2 ) , μ n (A/V^2), \mu _n (A/V2),μn为沟道中自由电子迁移率, C o x C_{ox} Cox为栅极下氧化层的单位面积电容, W为沟道宽度, L为沟道长度. 此时MOS管的漏源极间可看成是在 v G S v_{GS} vGS控制下的可变电阻 R o n R_{on} Ron, 其等效电路如图:

当 v D S v_{DS} vDS较小时, v D S 2 v_{DS}^2 vDS2可以忽略, 忽略后的式子表明在 v D S v_{DS} vDS较小时, i D i_{D} iD与 v D S v_{DS} vDS成近似线性关系. - 饱和区: v G S > V t h , V t h > v G D v_{GS}>V_{th}, V_{th}>v_{GD} vGS>Vth,Vth>vGD, 漏源区间的导电沟道被夹断. 在产生预夹断之后, i D i_D iD基本不随 v D S v_{DS} vDS的增加而增加, 形成饱和区(恒流区). 饱和区和可变电阻区的分界为预夹断, 即 v G D = v G S − v D S = V t h v_{GD}=v_{GS}-v_{DS}=V_{th} vGD=vGS−vDS=Vth, 将 v D S = v G S − V t h v_{DS}=v_{GS}-V_{th} vDS=vGS−Vth带入上面的 i D i_D iD表达式可得下式 i D = k p 2 ⋅ W L ( v G S − V t h ) 2 − − − v G S > V t h , v D S = v G S − V t h i_D=\frac{k_p}{2}\cdot \frac{W}{L}(v_{GS}-V_{th})^2---v_{GS}>V_{th}, v_{DS}=v_{GS}-V_{th} iD=2kp⋅LW(vGS−Vth)2−−−vGS>Vth,vDS=vGS−Vth该式描述的是 i D i_D iD是MOS管键入饱和工作状态后的 i D i_D iD, 该值对应 i D = f ( v D S ) i_D=f(v_{DS}) iD=f(vDS)特性曲线上的拐点. 根据前面的分析, 沟道夹断后, 随着 v D S v_{DS} vDS的增大, 剩余导电沟道上的电压基本不变, 如果仅考虑这一点, 在MOS进入饱和区后, i D i_D iD将保持刚进入饱和区时的数值, 即上式, 即 i D i_D iD与 v G S v_{GS} vGS呈二次函数关系, 与 v D S v_{DS} vDS无关, 输出特性曲线是一条直线. 实际上, 随着 v D S v_{DS} vDS的增大, 剩余沟道长度有所缩短, 沟道电阻也随之有所减小, 这使 i D i_D iD也会随着 v D S v_{DS} vDS增加而稍有增加, 这称为沟道长度调制效应, 一般沟道长度L越短, 沟道长度调制效应越严重. 一般情况下, 饱和区内 i D i_D iD随 v D S v_{DS} vDS增加而增大的增量与 v D S v_{DS} vDS的增量之间近似呈线性关系, 为描述沟道长度调制效应, 引入沟道长度调制因子 λ \lambda λ. λ越大, 沟道长度调制效应的影响程度就越严重. 通常λ在 ( 0.001 (0.001 (0.001~ 0.03 ) / V 0.03)/V 0.03)/V之间. i D = k p 2 W L ( v G S − V t h ) 2 ⋅ ( 1 + λ ⋅ v D S ) − − − v G S > V t h , v D S > v G S − V t h i_D=\frac{k_p}{2}\frac{W}{L}(v_{GS}-V_{th})^2\cdot (1+\lambda \cdot v_{DS})---v_{GS}>V_{th}, v_{DS}>v_{GS}-V_{th} iD=2kpLW(vGS−Vth)2⋅(1+λ⋅vDS)−−−vGS>Vth,vDS>vGS−Vth
参照双极型晶体管对基区调宽效应的描述方法, 在进行场效应管放大电路交流分析时, 引用厄尔利电压 V A V_A VA和微变输出电阻 r d s r_{ds} rds来描述沟道长度调制效应. 将饱和区内输出特性曲线向 v D S v_{DS} vDS的负值方向延长, 与 v D S v_{DS} vDS轴交于 − V A -V_A −VA点, V A V_A VA称为厄尔利电压. V A V_A VA越大, 饱和区内的 i D i_D iD曲线越平缓, 沟道长度调制效应越小.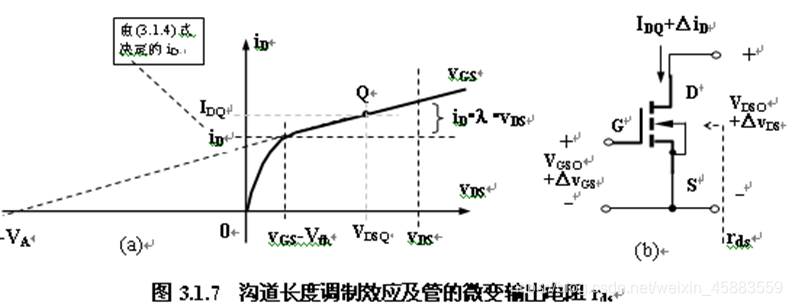
根据上图, 工作在饱和区的MOS管的沟道长度调制效应可等效为漏源极间的微变输出电阻 r d s r_{ds} rds, 由于 λ ≈ 1 / V A \lambda\approx 1/V_A λ≈1/VA, 微变等效电阻 r d s r_{ds} rds的表达式为 r d s = Δ v D S Δ i D ∣ I D Q V D S Q = V D S Q + V A I D Q ≈ V A I D Q = 1 λ ⋅ I D Q r_{ds}=\frac{\Delta v_{DS}}{\Delta i_D}|_{I_{DQ}\ V_{DSQ}}=\frac{V_{DSQ}+V_A}{I_{DQ}}\approx \frac{V_A}{I_{DQ}}=\frac{1}{\lambda\cdot I_{DQ}} rds=ΔiDΔvDS∣IDQ VDSQ=IDQVDSQ+VA≈IDQVA=λ⋅IDQ1
增强型NMOS管转移特性曲线
转移特性曲线反映了场效应管在截止区和饱和区内输出电流 i D i_D iD和输入电压 v G S v_{GS} vGS的关系. 在 v G S ≤ V t h v_{GS}\leq V_{th} vGS≤Vth的范围, 场效应管处于截止区, i D i_D iD基本为0, 在饱和区, 当 v D S v_{DS} vDS为大于 v G S − V t h v_{GS}-V_{th} vGS−Vth的某一固定值时, i D = f ( v G S , V D S Q ) i_D=f(v_{GS},V_{DSQ}) iD=f(vGS,VDSQ)由上面的式子确定, 输出电流与输入电压是二次函数关系, 而双极型晶体管在放大区输出电流 i C i_C iC与输入电压 v B E v_{BE} vBE呈指数关系. 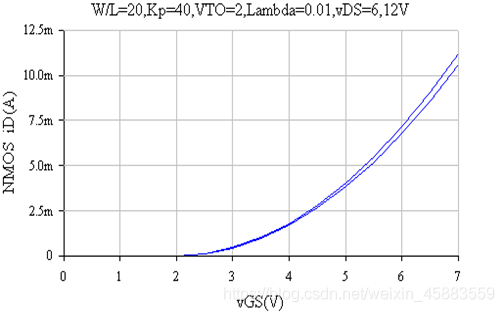
为描述输出电流与输入电压的关系, 定义微变跨导 g m g_m gm为 g m = Δ i D Δ v G S ∣ v G S = V G S Q i D = I D Q v D S = V D S Q g_m=\frac{\Delta i_D}{\Delta v_{GS}}|_{v_{GS}=V_{GSQ}\ i_D=I_{DQ}\ v_{DS}=V_{DSQ}} gm=ΔvGSΔiD∣vGS=VGSQ iD=IDQ vDS=VDSQ
在转移特性曲线上, g m g_m gm是直流工作点处的斜率. 当场效应管工作在饱和区, 且不考虑长度调制效应时, g m = l p W L ( V G S Q − V t h ) = 2 k p W L I D Q = 2 I D Q V G S Q − V t h g_m=l_p\frac{W}{L}(V_{GSQ}-V_{th})=\sqrt{2k_p\frac{W}{L}I_{DQ}}=\frac{2I_{DQ}}{V_{GSQ}-V_{th}} gm=lpLW(VGSQ−Vth)=2kpLWIDQ=VGSQ−Vth2IDQ
考虑沟道长度调制效应时, g m = l p W L ( V G S Q − V t h ) ( 1 + λ V D S Q ) = 2 k p W L I D Q ( 1 + λ V D S Q ) = 2 I D Q V G S Q − V t h g_m=l_p\frac{W}{L}(V_{GSQ}-V_{th})(1+\lambda V_{DSQ})=\sqrt{2k_p\frac{W}{L}I_{DQ}(1+\lambda V_{DSQ})}=\frac{2I_{DQ}}{V_{GSQ}-V_{th}} gm=lpLW(VGSQ−Vth)(1+λVDSQ)=2kpLWIDQ(1+λVDSQ)=VGSQ−Vth2IDQ
一般情况下, λ V D S Q \lambda V_{DSQ} λVDSQ远小于1, 所以在对场效应管进行功能呢分析时多采用不考虑沟道长度调制效应的式子计算.
在相同静态工作点情况下, MOS管 g m g_m gm的数值通常会比双极型晶体管小一二个数量级, 这是MOS管的一个缺点
MOS场效应管衬底调制效应
在MOS管正常工作时, 源区, 漏区, 导电沟道与衬底之间的PN结不应出现正向导通的情况, 这要求增强型NMOS管的衬, 源极之间电压 v B S v_{BS} vBS应满足 v B S ≤ 0 v_{BS}\leq 0 vBS≤0, 增强型PMOS则为 v B S ≥ 0 v_{BS}\geq 0 vBS≥0. 在集成电路中, 同类型的MOS管都集成在公共衬底上, 由于MOS管功能不同, 难以保证各MOS管的源极都与衬底短接,对那些不与衬底短接的NMOS管, 衬底, 源极之间存在负值电压 v B S v_{BS} vBS, 且 v B S v_{BS} vBS可能是变化的. 当 v B S < 0 v_{BS}<0 vBS<0时, 源区, 漏区及导电沟道与衬底之间的PN结反偏电压增加, 其耗尽层也增厚, 导电沟道因而变薄, 导电电阻增加, 使 i D i_D iD减小. 在导电沟道未形成时, v B S v_{BS} vBS也会使初建反型层的开启电压 V t h V_{th} Vth增大. v B S v_{BS} vBS对 i D i_D iD的影响称为衬底调制效应. 可通过参数背栅跨导 g m b g_{mb} gmb来描述衬底调制效应的大小. 一般情况下, g m b = η ⋅ g m g_{mb}=\eta \cdot g_m gmb=η⋅gm其中η称为跨到比常数, η一般在0.1~0.2范围之内. 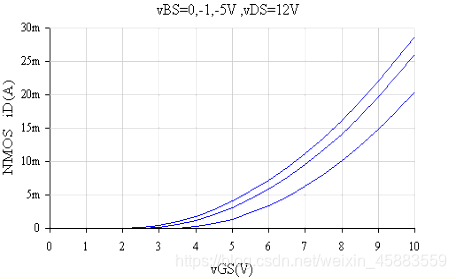
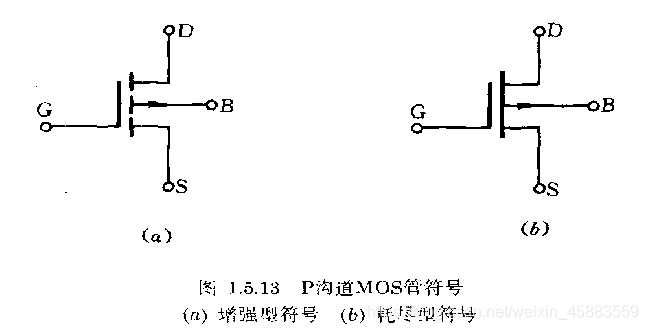
PMOS场效应管
增强型PMOS管的结构与增强型NMOS管的结构基本相同, 只有PMOS管衬底为N型半导体, 源区, 漏区及反型层导电沟道为P型半导体 . PMOS管所有电压, 电流均与NMOS管反向.
由于空穴载流子迁移率 μ p \mu_p μp比电子载流子 μ N \mu_N μN迁移率低, 这使得PMOS管的沟道电阻比NMOS管大, 工作速度比NMOS管低, 微变跨导也比NMOS的低. 集成电路中通常以PMOS管配合NMOS管工作, 构成互补MOS电路, 简称CMOS电路
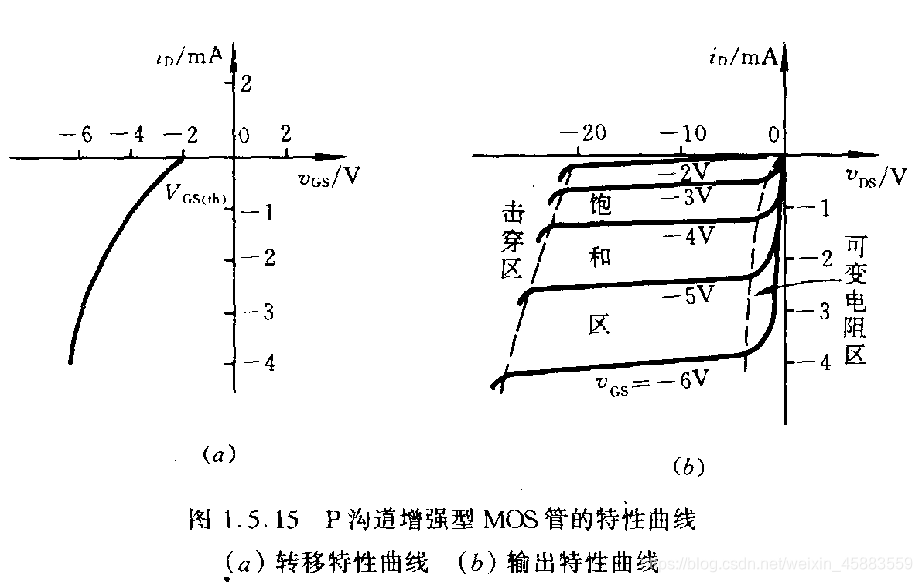
耗尽型场效应管
- 特性曲线
耗尽型场效应管与增强型MOS管结构基本相同, 通过特殊工艺直接在栅极下方生成反型层, 其反型层将源区, 漏区连通构成内建初始导电沟道.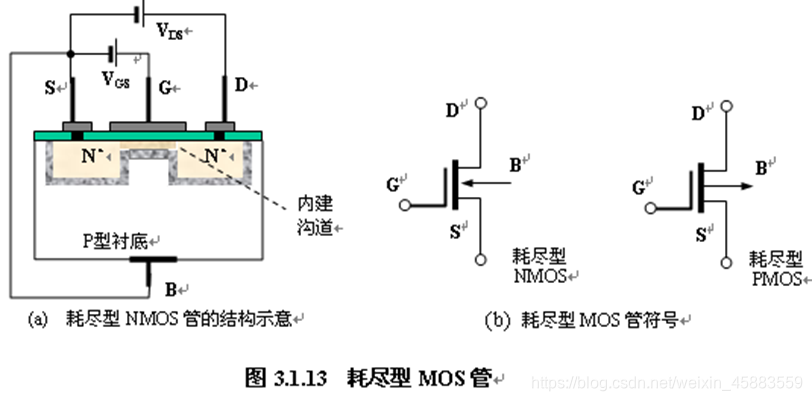
对于耗尽型NMOS管, 在 v D S v_{DS} vDS为某一较小的固定值, MOS管仍处于可变电阻区, 当 v G S v_{GS} vGS增加时, 栅极电位升高, 吸引源区, 漏区及衬底中更多电子聚集到栅极下, 使N型反型层导电沟道增厚, 导电电阻减小, i D i_D iD增大. 当 v G S v_{GS} vGS反向增大时, 栅极电位为负, 排斥电子, 使导电沟道变薄, 导电电阻增大, 电流 i D i_D iD减小. 当 v G S v_{GS} vGS反向增大到 V G S ( o f f ) V_{GS(off)} VGS(off)时, 反型层变薄到刚好消失, 电流 i D i_D iD减小到零, 称此时的 v G S = v G S ( o f f ) v_{GS}=v_{GS(off)} vGS=vGS(off)为夹断电压, 简写为 V o f f V_{off} Voff. 转移特性曲线如下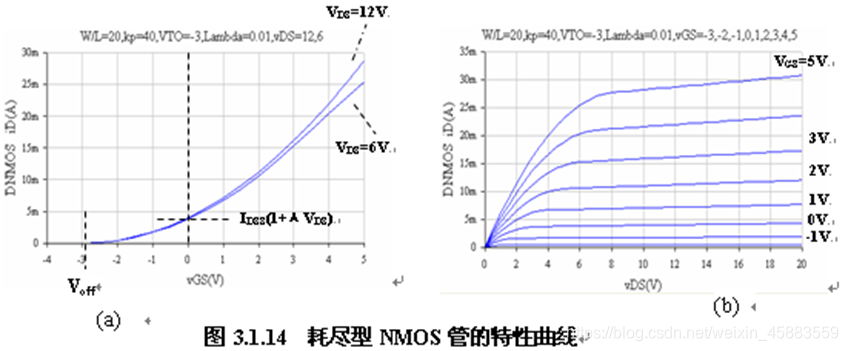
当 v G S > V o f f , 0 < v D S < v G S − V o f f v_{GS}>V_{off},0<v_{DS}<v_{GS}-V_{off} vGS>Voff,0<vDS<vGS−Voff时, MOS管处于可变电阻区, i D = f ( v D S , v G S ) i_D=f(v_{DS},v_{GS}) iD=f(vDS,vGS)关系如下 i D = k p 2 ⋅ W L [ 2 ( v G S − V o f f ) v D S − v D S 2 ] − − − v G S > V o f f , 0 < v D S < v G S − V o f f i_D=\frac{k_p}{2}\cdot \frac{W}{L}[2(v_{GS}-V_{off})v_{DS}-v_{DS}^2]---v_{GS}>V_{off}, 0<v_{DS}<v_{GS}-V_{off} iD=2kp⋅LW[2(vGS−Voff)vDS−vDS2]−−−vGS>Voff,0<vDS<vGS−Voff
当 v G S > V o f f , v D S > v G S − V o f f v_{GS}>V_{off}, v_{DS}>v_{GS}-V_{off} vGS>Voff,vDS>vGS−Voff时MOS管处于饱和区, 不考虑长度调制效应时, i D i_D iD表达式如下:
i D = k p 2 ⋅ W L ( v G S − V o f f ) 2 − − − v G S > V o f f , v D S > v G S − V o f f i_D=\frac{k_p}{2}\cdot \frac{W}{L}(v_{GS}-V_{off})^2---v_{GS}>V_{off}, v_{DS}>v_{GS}-V_{off} iD=2kp⋅LW(vGS−Voff)2−−−vGS>Voff,vDS>vGS−Voff
当 v G S = 0 v_{GS}=0 vGS=0时, 对应的可变电阻区与饱和区交界处 v D S = v G S − V o f f = − V o f f v_{DS}=v_{GS}-V_{off}=-V_{off} vDS=vGS−Voff=−Voff的漏极电流 i D i_D iD称为漏极饱和电流 I D S S I_{DSS} IDSS, 如果忽略沟道长度调制效应, 可令 v G S = 0 v_{GS}=0 vGS=0, 直接根据可变电阻区 i D i_D iD表达式可求出 I D S S I_{DSS} IDSS
I D S S = k p 2 ⋅ W L V o f f 2 I_{DSS}=\frac{k_p}{2}\cdot \frac{W}{L}V_{off}^2 IDSS=2kp⋅LWVoff2
引入漏极饱和电流 I D S S I_{DSS} IDSS后, 饱和区内的 i D i_D iD表达式为
i D = I D S S ( 1 − v G S V o f f ) 2 − − − v G S > V o f f , v D S > v G S − V o f f i_D=I_{DSS}(1-\frac{v_{GS}}{V_{off}})^2---v_{GS}>V_{off}, v_{DS}>v_{GS}-V_{off} iD=IDSS(1−VoffvGS)2−−−vGS>Voff,vDS>vGS−Voff
饱和区内, 耗尽型MOS管的微变跨导 g m g_m gm表达式定义和增强型相同, 可得基于 I D S S I_{DSS} IDSS的微变跨导为 g m g_m gm为
g m = − 2 I D S S V o f f ( 1 − V G S Q V o f f ) = − 2 V o f f I D S S ⋅ I D Q = 2 I D Q V G S Q − V o f f g_m=\frac{-2I_{DSS}}{V_{off}}(1-\frac{V_{GSQ}}{V_{off}})=\frac{-2}{V_{off}}\sqrt{I_{DSS}\cdot I_{DQ}}=\frac{2I_{DQ}}{V_{GSQ}-V_{off}} gm=Voff−2IDSS(1−VoffVGSQ)=Voff−2IDSS⋅IDQ=VGSQ−Voff2IDQ
P沟道耗尽型MOS管的特性类似增强型PMOS管, 但其加断电压 V o f f V_{off} Voff为正值. 放大应用中, 漏极电位应低于源极, 漏极电流 i D i_D iD的实际流向为流出漏极.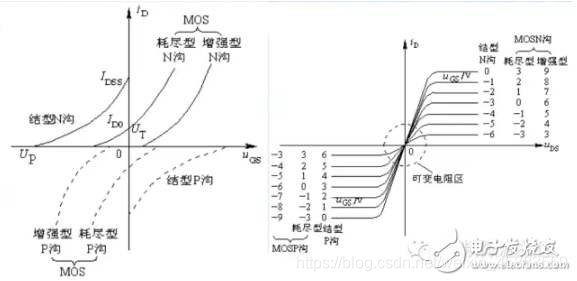
结型场效应管
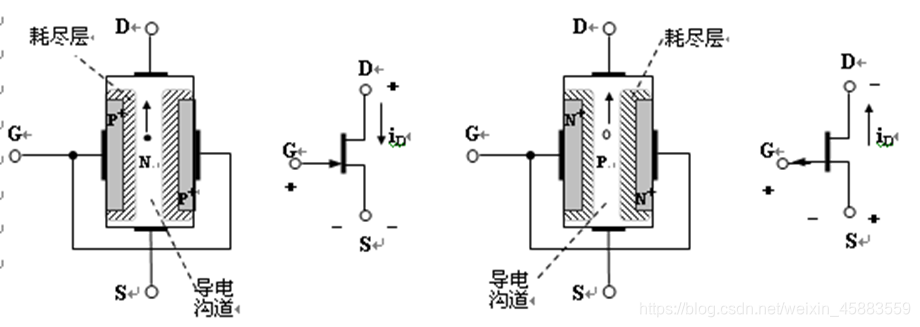
- 栅源电压 v G S v_{GS} vGS对沟道的影响.
为保证PN结反偏, v G S v_{GS} vGS必须小于0. 当漏源电压 v D S v_{DS} vDS等于0时, v G S v_{GS} vGS越大, 耗尽层就越宽, 导电沟道的有效宽度就越窄, 沟道电阻就越大. 当 v G S v_{GS} vGS增大到 ∣ V G S ( o f f ) ∣ |V_{GS(off)}| ∣VGS(off)∣时, (对于NJFET, V G S ( o f f ) V_{GS(off)} VGS(off)为负值), 导电沟道完全被耗尽层占据, 有效厚度减少至0, 称此状态为全夹断, 漏源电流 i D i_D iD为0, 漏源极间断路, V G S ( o f f ) V_{GS(off)} VGS(off)称为夹断电压. - 漏源电压 v D S v_{DS} vDS对沟道的影响
当 0 < v D S < v G S − V o f f 0<v_{DS}<v_{GS}-V_{off} 0<vDS<vGS−Voff时, 栅漏极间耗尽层厚度大于栅源极间耗尽层厚度. 此时场效应管工作在可变电阻区, 沟道电流与 v D S , v G D v_{DS},v_{GD} vDS,vGD的关系是
i D = I D S S [ − 2 ( 1 − v G S V o f f ) v D S V o f f − ( v D S V o f f ) 2 ] − − − V o f f < v G S ≤ 0 , 0 < v D S ≤ v G S − V o f f i_D=I_{DSS}[-2(1-\frac{v_{GS}}{V_{off}})\frac{v_{DS}}{V_{off}}-(\frac{v_{DS}}{V_{off}})^2]---V_{off}<v_{GS}\leq0,0<v_{DS}\leq v_{GS}-V_{off} iD=IDSS[−2(1−VoffvGS)VoffvDS−(VoffvDS)2]−−−Voff<vGS≤0,0<vDS≤vGS−Voff
当 v D S v_{DS} vDS由零增大到 v G S − V o f f v_{GS}-V_{off} vGS−Voff时, 恰好使 v G D v_{GD} vGD增大到 v G D = − v D S + v G S = V o f f v_{GD}=-v_{DS}+v_{GS}=V_{off} vGD=−vDS+vGS=Voff时, 导电沟道在漏极一段被夹断, 称此状态为预夹断. 此状态下漏源电流如下, 式中的 v D S = v G S − V o f f v_{DS}=v_{GS}-V_{off} vDS=vGS−Voff. 当 v G S = 0 v_{GS}=0 vGS=0时的预夹断漏源电流称为饱和电流 I D S S I_{DSS} IDSS
i D = I D S S ( 1 − v G S V o f f ) 2 − − − 0 ≥ v G S > V o f f , v D S > v G S − V o f f i_D=I_{DSS}(1-\frac{v_{GS}}{V_{off}})^2---0\geq v_{GS}>V_{off}, v_{DS}>v_{GS}-V_{off} iD=IDSS(1−VoffvGS)2−−−0≥vGS>Voff,vDS>vGS−Voff
在预夹断发生后, 继续增大 v D S v_{DS} vDS的值, 加断点将向源极移动. 在 v D S v_{DS} vDS的作用下, 电子由源极沿导电沟道向漏极移动, 达到夹断区时被耗尽层内的强电场吸引继续向漏区漂移, 形成漏源电流 i D i_D iD, 当 v D S v_{DS} vDS增大时, 栅极到沟道加断点的电压总是 V o f f V_{off} Voff, 夹断点到到源极间剩余的导电沟道上的电压也总是 v G S − V o f f v_{GS}-V_{off} vGS−Voff. i D i_D iD基本保持不变
考虑到沟道预夹断后, 导电沟道会随 v D S v_{DS} vDS增大而减短, 沟道电阻也随之减小, 沟道电流会随 v D S v_{DS} vDS增大, 与MOS场效应管一样, 这种现象称为沟道长度调制效应, 引入沟道长度调质因子 λ \lambda λ或厄尔利电压来描述. 在进行交流分析时, 可用漏源极微变电阻 r d s r_{ds} rds表示沟道长度调制效应的影响. r d s = Δ v D S Δ i D ∣ I D Q V D S Q = V D S Q + V A I D Q ≈ V A I D Q = 1 λ ⋅ I D Q r_{ds}=\frac{\Delta v_{DS}}{\Delta i_D}|_{I_{DQ}\ V_{DSQ}}=\frac{V_{DSQ}+V_A}{I_{DQ}}\approx \frac{V_A}{I_{DQ}}=\frac{1}{\lambda\cdot I_{DQ}} rds=ΔiDΔvDS∣IDQ VDSQ=IDQVDSQ+VA≈IDQVA=λ⋅IDQ1
g m = − 2 I D S S V o f f ( 1 − V G S Q V o f f ) = − 2 V o f f I D S S ⋅ I D Q = 2 I D Q V G S Q − V o f f g_m=\frac{-2I_{DSS}}{V_{off}}(1-\frac{V_{GSQ}}{V_{off}})=\frac{-2}{V_{off}}\sqrt{I_{DSS}\cdot I_{DQ}}=\frac{2I_{DQ}}{V_{GSQ}-V_{off}} gm=Voff−2IDSS(1−VoffVGSQ)=Voff−2IDSS⋅IDQ=VGSQ−Voff2IDQ
结型场效应管的 r d s , g m r_{ds},g_m rds,gm与耗尽型MOS场效应管相同.
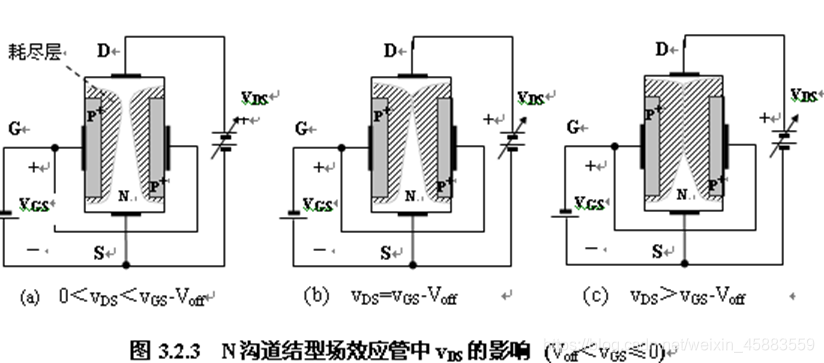
- 结型场效应管特性曲线:
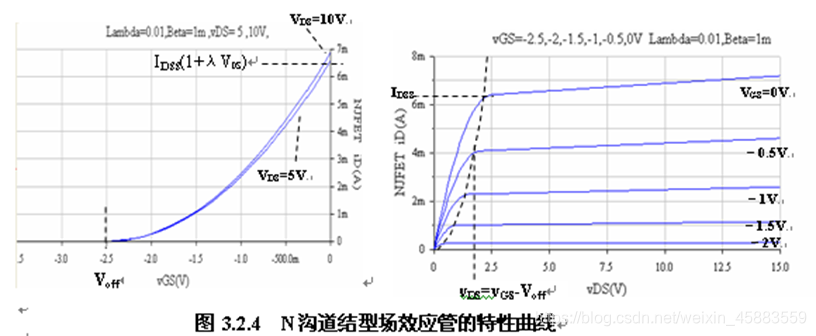
其转移特性曲线和输出特性曲线与耗尽型MOS管类似. 结型场效应管的输出特性曲线分为可变电阻去, 饱和区, 截止区, 击穿区. 可变电阻区和饱和区的分界为 v G D = V o f f , v D S = v G S − V o f f v_{GD}=V_{off}, v_{DS}=v_{GS}-V_{off} vGD=Voff,vDS=vGS−Voff, v G S = 0 v_{GS}=0 vGS=0对应的输出特性曲线的拐点位置的电流 i D i_D iD为饱和电流 I D S S I_{DSS} IDSS.
转移特性曲线反映了场效应管在截止区, 饱和区的 i D = f ( v G S ) i_D=f(v_{GS}) iD=f(vGS), 在 λ \lambda λ比较小或不考虑沟道长度调制效应时, 转移特性曲线上的 v G S = 0 v_{GS}=0 vGS=0对应的 i D i_D iD是饱和电流 I D S S I_{DSS} IDSS.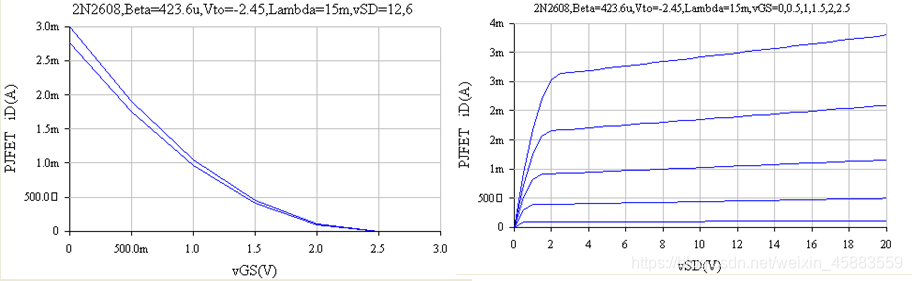
P沟道结型场效应管的特性曲线.
场效应管的放大电路
- 场效应管微变信号模型
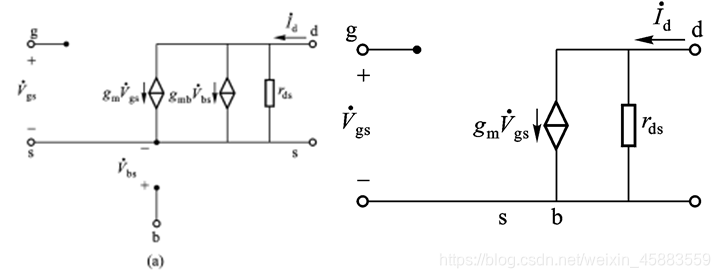
场效应管直流偏置电路
- 分压式偏置
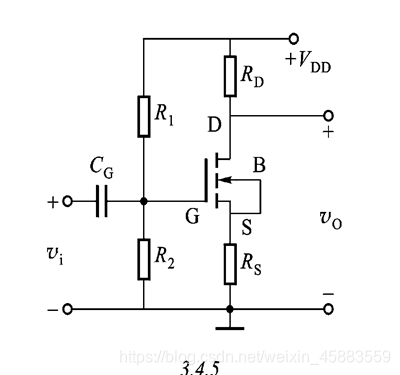
V G Q = R G 2 R G 1 + R G 2 V D D , V S Q = I D Q R S S V G S Q = V G Q − v S Q = R G 2 R G 1 + R G 2 V D D − I D Q R S S V_{GQ}=\frac{R_{G2}}{R_{G1}+R_{G2}}V_{DD},V_{SQ}=I_{DQ}R_{SS}\\[2ex] V_{GSQ}=V_{GQ}-v_{SQ}=\frac{R_{G2}}{R_{G1}+R_{G2}}V_{DD}-I_{DQ}R_{SS} VGQ=RG1+RG2RG2VDD,VSQ=IDQRSSVGSQ=VGQ−vSQ=RG1+RG2RG2VDD−IDQRSS - 自给偏压式偏置
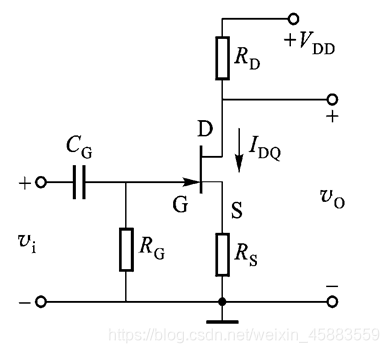
由于输入电阻极高, 栅极输入电流很小, 电阻 R C R_C RC两端的直流压降近似为零(也就是栅极电位 V G ≈ 0 V_G\approx 0 VG≈0), 因此 V G S Q = − V S Q = − I D Q R S V_{GSQ}=-V_{SQ}=-I_{DQ}R_{S} VGSQ=−VSQ=−IDQRS可根据耗尽型场效应管的 i D i_D iD与 v G S v_{GS} vGS函数关系解出 I D Q , V D S Q I_{DQ},V_{DSQ} IDQ,VDSQ
I D Q = I D S S ( 1 − v G S Q V o f f ) 2 = I D S S ( 1 − − I D Q R S S V o f f ) 2 V D S Q = V D D − I D Q ( R D + R S S ) I_{DQ}=I_{DSS}(1-\frac{v_{GSQ}}{V_{off}})^2=I_{DSS}(1-\frac{-I_{DQ}R_{SS}}{V_{off}})^2\\[2ex] V_{DSQ}=V_{DD}-I_{DQ}(R_{D}+R_{SS}) IDQ=IDSS(1−VoffvGSQ)2=IDSS(1−Voff−IDQRSS)2VDSQ=VDD−IDQ(RD+RSS) - 共源增益:
A v = − g m ( R D / / r d s ) R i = R G R o = R D / / r d s A_v=-g_m(R_D//r_{ds})\\[2ex] R_i=R_G\\[2ex] R_o=R_D//r_{ds} Av=−gm(RD//rds)Ri=RGRo=RD//rds - 共栅增益:
A v = g m ( R D / / R L ) R i = 1 g m R o = R D A_v=g_m(R_D//R_L)\\[2ex] R_i=\frac{1}{g_m}\\[2ex] R_o=R_D Av=gm(RD//RL)Ri=gm1Ro=RD - 共漏增益:
A v = g m R L ′ 1 + g m R L ′ R i = R G + R G 1 / / R G 2 R o = ( 1 g m ) / / ( 1 g m b ) / / r d s / / R S S A_v=\frac{g_mR_L'}{1+g_mR_L'}\\[2ex] R_i=R_G+R_{G1}//R_{G2}\\[2ex] R_o=(\frac{1}{g_m})//(\frac{1}{g_{mb}})//r_{ds}//R_{SS} Av=1+gmRL′gmRL′Ri=RG+RG1//RG2Ro=(gm1)//(gmb1)//rds//RSS
这篇关于场效应晶体管及其放大电路的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








