论文笔记：YOLOv3: An Incremental Improvement(yolo v3)

一、基本信息

标题：YOLOv3: An Incremental Improvement
时间：2018
引用格式：Redmon, Joseph, and Ali Farhadi. “Yolov3: An incremental improvement.” arXiv preprint arXiv:1804.02767 (2018).

二、研究背景

YOLOv1：
提出和R-CNN不同的方式，去掉检测Proposal步骤，利用网格划分粗略位置，然后使用回归预测进行微调。虽然速度很快，但是每个网格只有2个bbox，召回率和准确度都不太高。
YOLOv2：
Better：
Batch normalization 批归一化 训练上的改进
High Resolution Classifier 高分辨率图像微调分类模型 训练上的改进
Convolutional With Anchor Boxes 采用先验框 借鉴Faster R-CNN中Anchor
Dimension Clusters 聚类提取先验框尺度 对Anchor的改进
Fine-Grained Features 检测细粒度特征 训练上的改进
Multi-Scale Training 多尺度图像训练 训练上的改进
Faster：
使用Darknet-19，更快
Stronger：
利用WordTree实现检测9000中对象

三、创新点

YOLO3主要的改进有：
新的网络结构Darknet-53
利用多尺度特征进行对象检测
对象分类用Logistic取代了Softmax
改进后AP和AP-50对比:

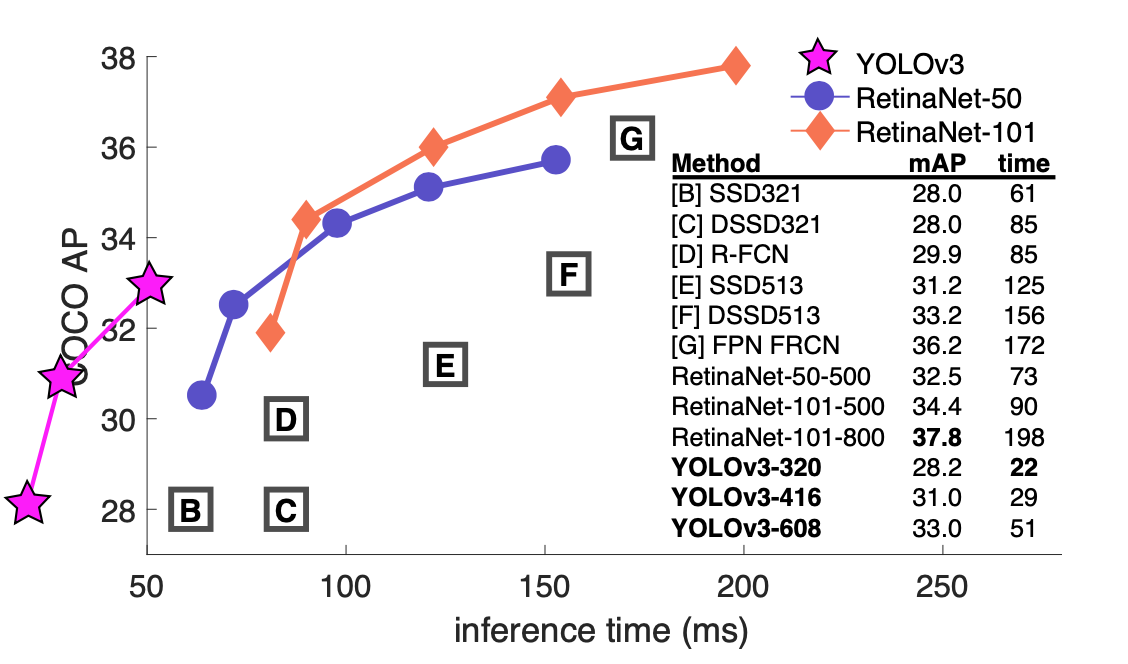
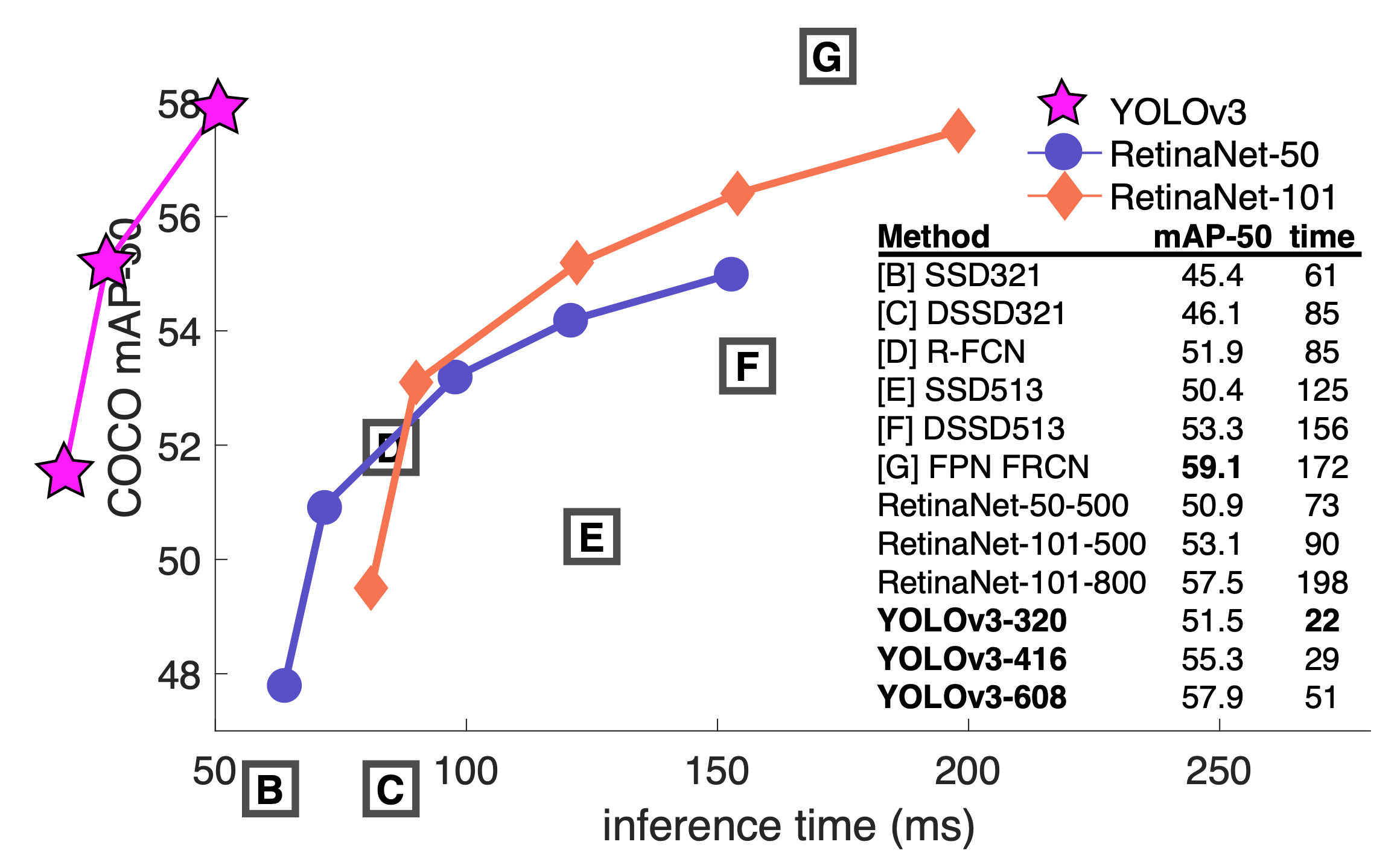
COOCO数据集中的AP和AP50是一种评价指标：

比如AP50是这么求的：
对检测到的结果按照IOU>50%的boxx认为是真正例(TP)，否则是假正例(FP)。
没有检测到又分为，实际存在即假负例(FN)，实际不存在即真假例(TN)。

由此可以按照11点法(11-point interpolated average precision)求AP。具体描述可以看这里。由此说来AP50后面的50是指IOU为50%。同理可以求AP70、AP80
而COCO中说的AP是AP[.50:.05:.95]，也就是IOU_T设置为0.5,0.55,0.60,0.65……0.95，算十个APx，然后再求平均，得到的就是P。
配合这篇博文可以更好理解COOCO中的AP、AP50、AP70

新的网络结构Darknet-53

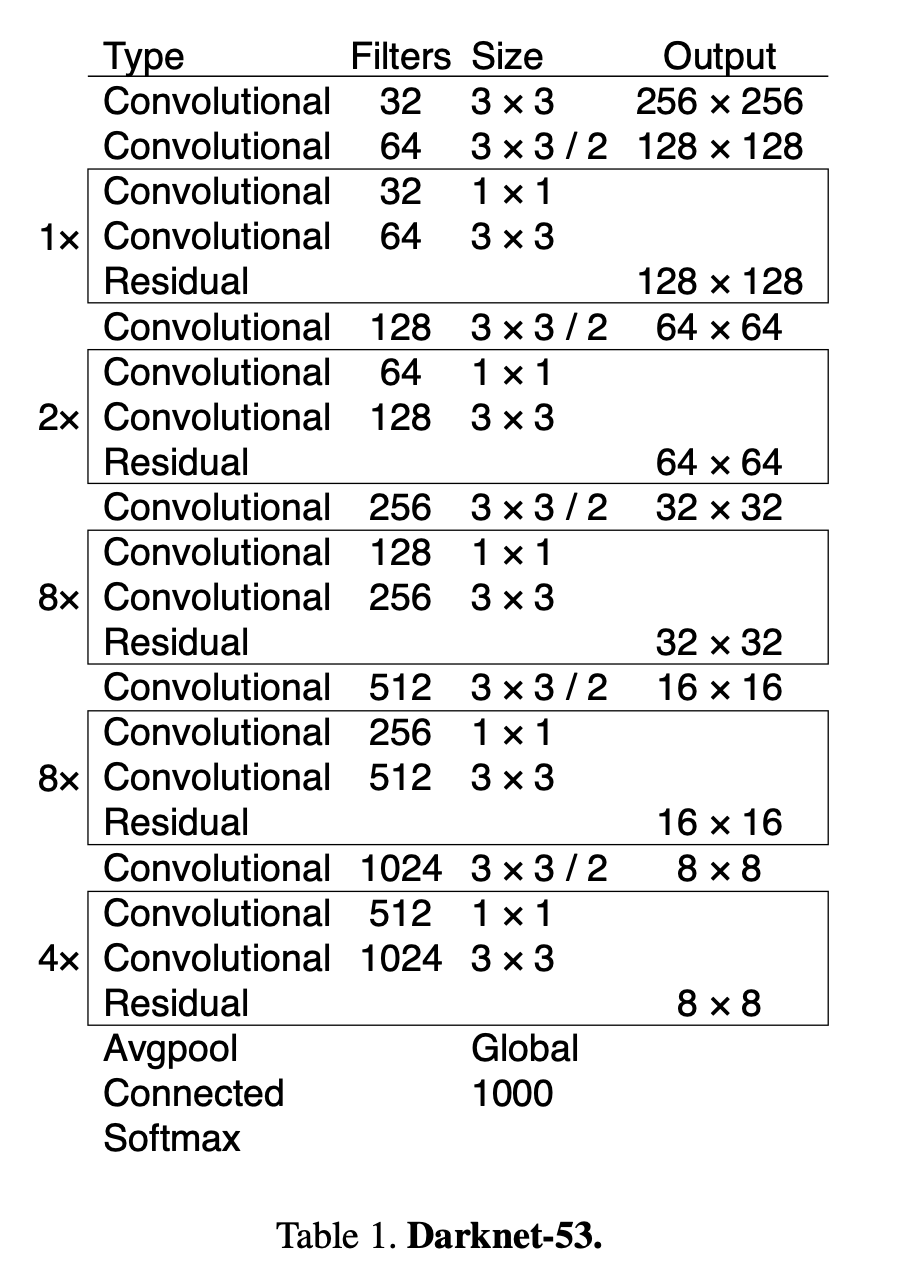
网络细节就没必要搞太清楚了，主要改进的地方是它借鉴了残差网络residual network的做法，在一些层之间设置了快捷链路（shortcut connections）。关于ResNet之前做过笔记，这里过一下ResNet的核心：Residual Block结构

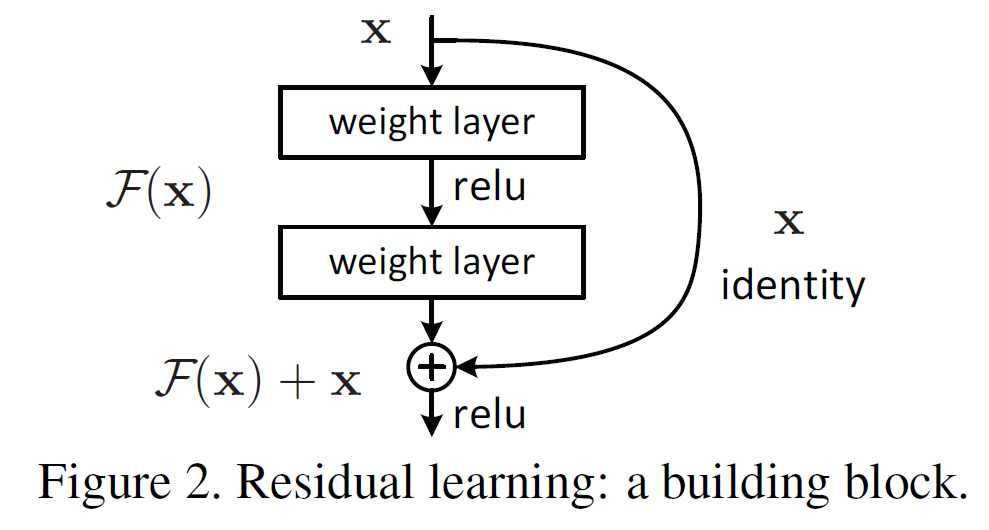
深度残差网络。如果深层网络的后面那些层是恒等映射，那么模型就退化为一个浅层网络。那现在要解决的就是学习恒等映射函数了。 但是直接让一些层去拟合一个潜在的恒等映射函数H(x) = x，比较困难，这可能就是深层网络难以训练的原因。但是，如果把网络设计为H(x) = F(x) + x,如上图。可以转换为学习一个残差函数F(x) = H(x) - x. 只要F(x)=0，就构成了一个恒等映射H(x) = x. 而且，拟合残差肯定更加容易。标识快捷连接既不增加额外的参数，也不增加计算复杂度。整个网络仍然可以通过带有反向传播的SGD进行端到端的训练。

利用多尺度特征进行对象检测

和Mask R-CNN一样利用了FPN结果来解决多尺度问题
所以先回顾一下FPN，这里记了FPN笔记:

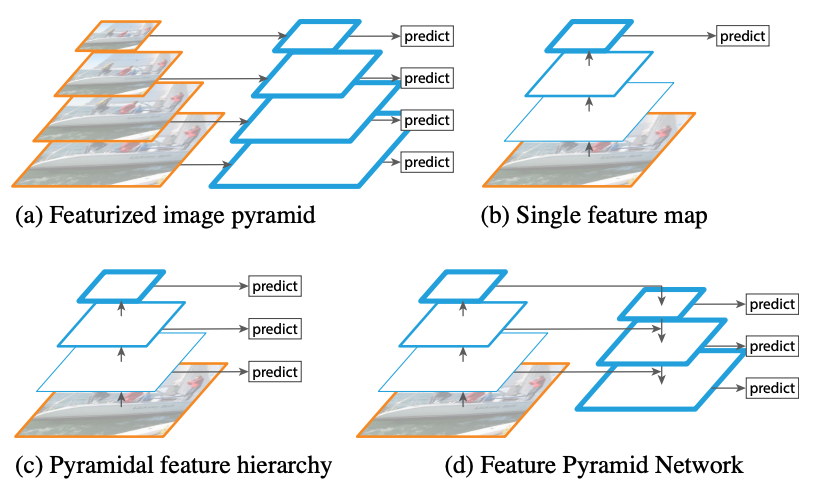
橙色框代表图片，一般由resize/下采样操作产生；蓝色框代表特征图，通过卷积产生，越粗的框代表语义越深。

( a ) 多维度图片输入，多维度特征图预测：图像金字塔，不同尺寸的图输入到网络，底层分辨率高，可以检测细节，高层分辨率低，可以检测轮廓
( b ) 单维度图片输入，单维度特征图预测：拿单层(这里是最后一层)的特征图进行预测，Fast/er R-CNN R-CNN，都是这种
( c ) 单维度图片输入，多维度特征图预测：和b相比除了拿最后一层外，还会从后往前多拿几层预测(比如SSD，但是SDD没有一直到前，所以SSD对于小物体检测也不是很准)
( d )单维度图片输入，多维度特征图预测：和c相比可以看到，本层会连接高层的语义，这样做的目的是使每一层不同尺度的特征图都具有较强的语义信息

然后对比看下用了FPN的Darknet-53网络结构：

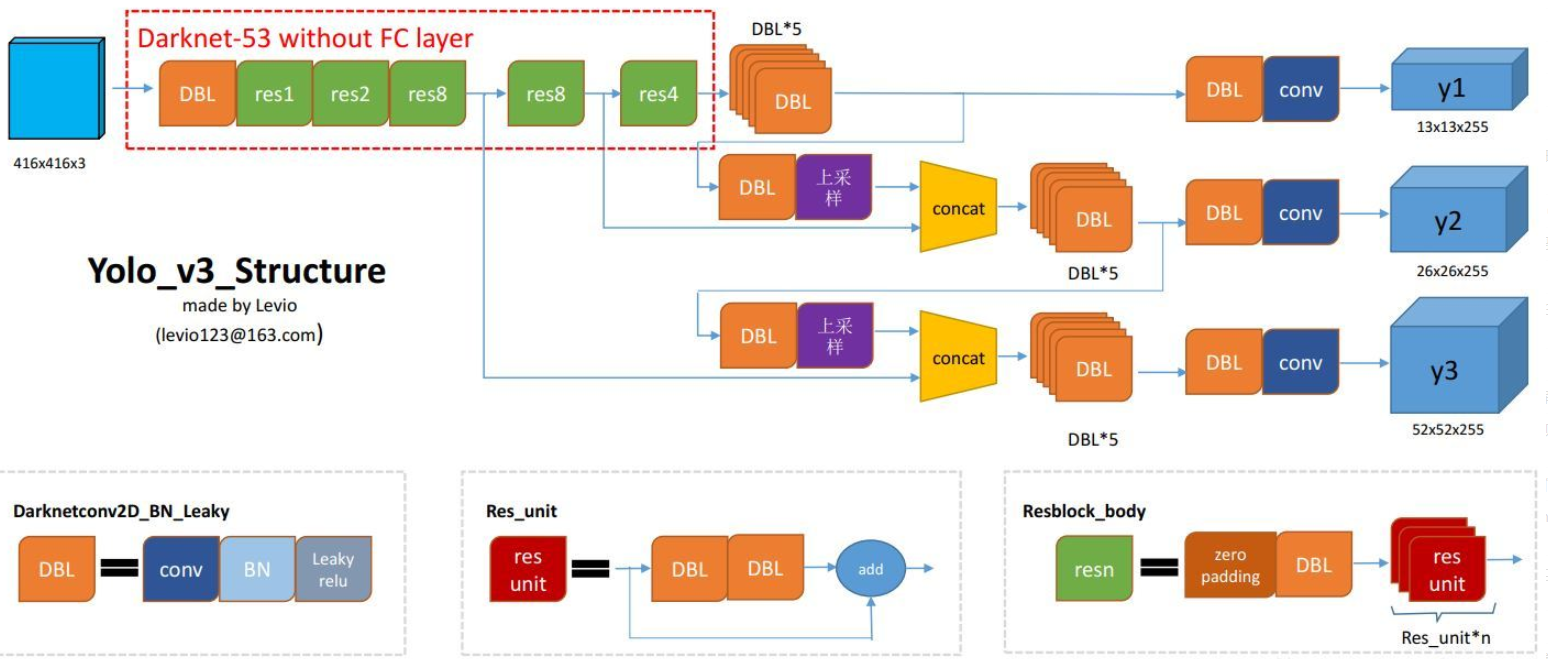
DBL:代码中的Darknetconv2d_BN_Leaky，是yolo_v3的基本组件。就是卷积+BN+Leaky relu。
resn：n代表数字，有res1，res2, … ,res8等等，表示这个res_block里含有多少个res_unit。
concat：张量拼接。将darknet中间层和后面的某一层的上采样进行拼接。拼接的操作和残差层add的操作是不一样的，拼接会扩充张量的维度，而add只是直接相加不会导致张量维度的改变。具体可以参考笔记加以理解。

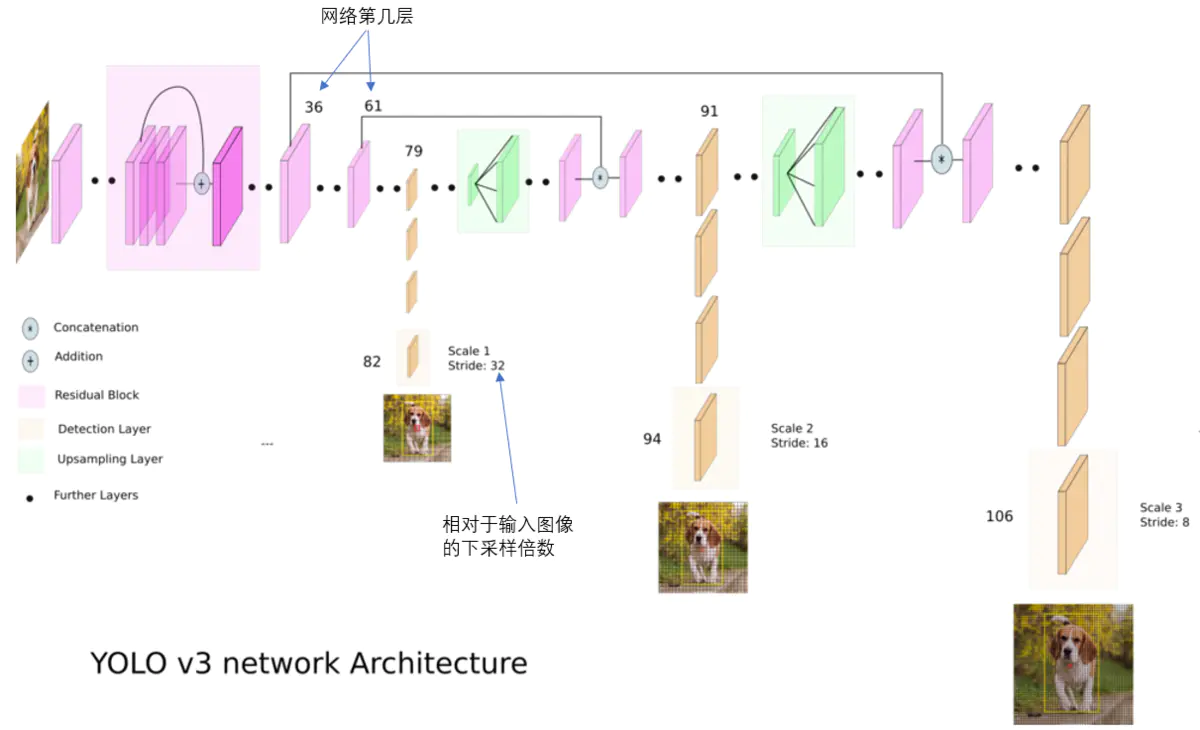
OLO2曾采用passthrough结构来检测细粒度特征，在YOLO3更进一步采用了3个不同尺度的特征图来进行对象检测。

结合上图看，卷积网络在79层后，经过下方几个黄色的卷积层得到一种尺度的检测结果。相比输入图像，这里用于检测的特征图有32倍的下采样。比如输入是416416的话，这里的特征图就是1313了。由于下采样倍数高，这里特征图的感受野比较大，因此适合检测图像中尺寸比较大的对象。

为了实现细粒度的检测，第79层的特征图又开始作上采样（从79层往右开始上采样卷积），然后与第61层特征图融合（Concatenation），这样得到第91层较细粒度的特征图，同样经过几个卷积层后得到相对输入图像16倍下采样的特征图。它具有中等尺度的感受野，适合检测中等尺度的对象。

最后，第91层特征图再次上采样，并与第36层特征图融合（Concatenation），最后得到相对输入图像8倍下采样的特征图。它的感受野最小，适合检测小尺寸的对象。

作者：X猪
链接：https://www.jianshu.com/p/d13ae1055302
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

9种尺度的先验框

既然使用了FPN，那么Anchor也要相应变化，不然3中尺度都用yolo v2中提供的5种聚类得到Anchor会不太合适。
所以，在3种尺度下，分别聚类3个就行了，即：
scale1：聚类得到3个Anchor
scale2：聚类得到3个Anchor
scale3：聚类得到3个Anchor
所以最后有9个Anchor。在3种尺度下对应使用。

在COCO数据集这9个先验框是：(10x13)，(16x30)，(33x23)，(30x61)，(62x45)，(59x119)，(116x90)，(156x198)，(373x326)。

分配上，在最小的1313特征图上（有最大的感受野）应用较大的先验框(116x90)，(156x198)，(373x326)，适合检测较大的对象。中等的2626特征图上（中等感受野）应用中等的先验框(30x61)，(62x45)，(59x119)，适合检测中等大小的对象。较大的52*52特征图上（较小的感受野）应用较小的先验框(10x13)，(16x30)，(33x23)，适合检测较小的对象。

对象分类用Logistic回归取代了Softmax回归

这里的logistic和softmax分别代表的是logistic回归和softmax回归。它们都是用回归(regression)方式来进行分类。
具体的logistic回归和softmax回归步骤可以具体看这个笔记Linner Regression、Logistic Regression、Softmax Regression区别与联系，专门花了几个小时整理。这里就不展开。

那么为什么要用Logistic回归取代了Softmax回归？

原文这么描述的：

Each box predicts the classes the bounding box may con- tain using multilabel classification. We do not use a softmax as we have found it is unnecessary for good performance, instead we simply use independent logistic classifiers. During training we use binary crosentropy loss for the class predictions.
This formulation helps when we move to more complex domains like the Open Images Dataset [7]. In this dataset there are many overlapping labels (i.e. Woman and Person). Using a softmax imposes the assumption that each box has exactly one class which is often not the case. A multilabel approach better models the data.

大意是softmax对性能提升没有很大帮助，而使用多个二元logistic分类器(instead we simply use independent logistic classifiers)可以取代softmax。类似单个神经元可以拟合复杂函数。

首先logistic是softmax的特殊情况，softmax是logistic一般情况。其次在类别不是独立的情况下，使用logistic更好。比如，要区分图像是风景、人和黑白图片。那么一张图有可能是黑白的人像图，即一个bbox包含多个标签(overlapping labels)，而使用softmax增强了一个假设，一个bbox只对应一种类。但是情况并非如此。多标签方法可以更好地模拟数据。

Softmax 回归 vs. k 个二元分类器
如果你在开发一个音乐分类的应用，需要对k种类型的音乐进行识别，那么是选择使用 softmax 分类器呢，还是使用 logistic 回归算法建立 k 个独立的二元分类器呢？
这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 k = 4 的softmax回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 k 设为5。）
如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声 。这种情况下，使用4个二分类的 logistic 回归分类器更为合适。这样，对于每个新的音乐作品 ，我们的算法可以分别判断它是否属于各个类别。
现在我们来看一个计算视觉领域的例子，你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是：室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢？ (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片，你又会选择 softmax 回归还是多个 logistic 回归分类器呢？
在第一个例子中，三个类别是互斥的，因此更适于选择softmax回归分类器 。而在第二个例子中，建立三个独立的 logistic回归分类器更加合适。

简单总结一下：
什么要替换：用softmax regression引入一个假设，即softmax中max含义，即一个box只能预测一个类。而事实上一个box可以多个类，比如在女人和人。
它们之间关系：个人认为softmax regression就是logistic regression的多类别表示。而softmax函数有冗余参数集，所以softmax regression可以转为logistic regression，或者说logistic regression是softmax regression的一个特例。
从另一种角度来说多个logistic regression(二元分类器)可以替代softmax regression多类预测。类似多个神经元可以拟合复杂函数。

损失函数

损失函数为：
$$\begin{array}{l}\text{ Loss }={\lambda }_{\text{coord }}{\sum }_{i=0}^{S^2}{\sum }_{j=0}^B{I}_{ij}^{obj}\left[{\left(x_i-{\hat{x}}_i^j\right)}^2+{\left(y_i-{\hat{y}}_i^j\right)}^2\right]+\\ \\ {\lambda }_{\text{coord }}{\sum }_{i=0}^{S^2}{\sum }_{j=0}^B{I}_{ij}^{obj}\left[{\left(\sqrt{w_i^j}-\sqrt{{\hat{w}}_i^j}\right)}^2+{\left(\sqrt{h_i^j}-\sqrt{{\hat{h}}_i^j}\right)}^2\right]-\\ \\ {\sum }_{i=0}^{S^2}{\sum }_{j=0}^B{I}_{ij}^{obj}\left[{\hat{C}}_i^j\log \left(C_i^j\right)+\left(1-{\hat{C}}_i^j\right)\log \left(1-C_i^j\right)\right]-\\ \\ {\lambda }_{\text{noobj }}{\sum }_{i=0}^{S^2}{\sum }_{j=0}^B{I}_{ij}^{\text{noobj }}\left[{\hat{C}}_i^j\log \left(C_i^j\right)+\left(1-{\hat{C}}_i^j\right)\log \left(1-C_i^j\right)\right]-\\ \\ {\sum }_{i=0}^{S^2}{I}_i^{\text{obj }}{\sum }_{c\in \text{ classes }}(\left[{\hat{P}}_i^j\log \left(P_i^j\right)+\left(1-{\hat{P}}_i^j\right)\log \left(1-P_i^j\right)\right]\end{array}$$

网格一共是$S\ast S$个，每个网格产生$B$个候选框anchor box，每个候选框会经过网络最终得到相应的bounding box。最终会得到$S\ast S\ast B$个bounding box

下面解释公式中的含义，大部分与yolo1一样：
$I_i^{obj}$ 意思是网格i中存在对象。除了i以外的gird，都不能预测该对象。即一个Object只由一个grid负责预测，不要多个grid都抢着预测同一个Object

$I_{ij}^{obj}$ 意思是网格i的第j个bounding box中存在对象。 除了j以外的bbox，都不能代表该对象。即一个Object只会选择一个具有最大IOU的bbox负责这个Object。

$I_{ij}^{noobj}$ 意思是网格i的第j个bounding box中不存在对象。

网格负责(responsible) 的解释：
具体就是计算出该Object的bounding box的中心位置，这个中心位置落在哪个grid，该grid对应的输出向量中该对象的类别概率是1（该gird负责预测该对象），所有其它grid对该Object的预测概率设为0（不负责预测该对象）。

bbox负责(responsible) 的解释：
公式：$Confidence=Pr(Object)\ast IO{U}_{pred}^{truth}$
看9个bounding box的IOU，哪个比较大（更接近对象实际的bounding box），就由哪个bounding box来负责预测该对象是否存在，即该bounding box的$Pr(Object)=1$，同时对象真实bounding box的位置也就填入该bounding box。剩余不负责预测的bounding box的$Pr(Object)=0$。
总的来说就是，与对象实际bounding box最接近的那个bounding box，其$Confidence=IO{U}_{pred}^{truth}$，该网格的其它bounding box的$Confidence=0$。

论文中是这么规定正负样本的，但是我看代码是，只要目标所在网格产生的9个anchor中和目标的真实框的iou大于阈值的就为正样本，如果都小于阈值，那么和目标iou最大的为正样本。来自这里的解释

拆开每项来看：

中心坐标误差
$${\lambda }_{\text{coord }}\sum _{i=0}^{S^2}\sum _{j=0}^B{\mathbb{I}}_{ij}^{\text{obj }}\left[{\left(x_i-{\hat{x}}_i\right)}^2+{\left(y_i-{\hat{y}}_i\right)}^2\right]$$
和yolo1一样
有在$1_{ij}^{\mathrm{o}\mathrm{b}\mathrm{j}}=1$时，也就是网格i的第j个bounding box中存在对象，网格才计入误差。

实际上，网络输出的应当是 $t_x$ 和 $t_y,$ 然后通过 $\sigma \left(t_x\right)$ 和 $\sigma \left(t_y\right),$ 再乘以步长，就映射到了输入大小的图上的目标了，所以在计算误差的时候，其实也是用的这一项 $\sigma \left(t_x\right)\ast$ stride和 $\sigma \left(t_y\right)\ast$ stride和真实目标经过resize到416 * 416上的目标的大小，去计算误差。

宽高坐标误差

$${\lambda }_{\text{coord }}\sum _{i=0}^{S^2}\sum _{j=0}^B{I}_{ij}^{obj}\left[{\left(\sqrt{w_i^j}-\sqrt{{\hat{w}}_i^j}\right)}^2+{\left(\sqrt{h_i^j}-\sqrt{{\hat{h}}_i^j}\right)}^2\right]$$
和yolo1一样
边框宽度，高度误差，只有在$I_{ij}^{\mathrm{o}\mathrm{b}\mathrm{j}}=1$时，也就是网格i的第j个bounding box中存在对象，网格才计入误差。

宽度和高度先取了平方根，因为如果直接取差值的话，大的对象对差值的敏感度较低，小的对象对差值的敏感度较高，所以取平方根可以降低这种敏感度的差异，使得较大的对象和较小的对象在尺寸误差上有相似的权重。

实际上，网络输出的应当是 $\left(t_w\right)$ 和 $\left(t_h\right),$ 所以在计算误差的时候，其实也是用的这一项 $\left(t_w\right)\ast$ stride和 $\left(t_h\right)\ast$ stride和真实目标经过resize之后的值，去计算误差的。所以可以认为公式里的 $w_i$ 就是 $\left(t_w\right)\ast$ stride等等。

置信度误差(存在对象)
$$\begin{array}{c}-{\sum }_{i=0}^{S^2}{\sum }_{j=0}^B{I}_{ij}^{obj}\left[{\hat{C}}_i^j\log \left(C_i^j\right)+\left(1-{\hat{C}}_i^j\right)\log \left(1-C_i^j\right)\right]\end{array}$$
由于yolov3中剔除了softmax改用logistic，分类损失换成了交叉熵。
带有 $I_{ij}^{Ibj}$ 意味着只有"负责"（IOU比较大）预测的那个bounding box的置信度才会计入误差。

置信度误差(不存在对象)
$$-{\lambda }_{\text{noobj}}\sum _{i=0}^{S^2}\sum _{j=0}^B{I}_{ij}^{\text{noobj}}\left[{\hat{C}}_i^j\log \left(C_i^j\right)+\left(1-{\hat{C}}_i^j\right)\log \left(1-C_i^j\right)\right]$$
由于yolov3中剔除了softmax改用logistic，分类损失换成了交叉熵
不存在对象的bounding box的置信度误差。因为不存在对象的bounding box应该老老实实的说"我这里没有对象"，也就是输出尽量低的置信度。如果它不恰当的输出较高的置信度，会与真正"负责"该对象预测的那个bounding box产生混淆。其实就像对象分类一样，正确的对象概率最好是1，所有其它对象的概率最好是0。

所以不管anchor box是否负责某个目标，都会计算置信度误差。

分类误差
$$-\sum _{i=0}^{S^2}{I}_{ij}^{obj}\sum _{c\in \text{classes}}(\left[{\hat{P}}_i^j\log \left(P_i^j\right)+\left(1-{\hat{P}}_i^j\right)\log \left(1-P_i^j\right)\right]$$
对象分类误差，只有在$I_{ij}^{\mathrm{o}\mathrm{b}\mathrm{j}}=1$时，也就是网格i的第j个bounding box中存在对象，网格才计入误差。
分类误差也是选择了交叉熵作为损失函数。

和yolo1一样：
乘以 ${\lambda }_{coord}$ 调节bounding box位置误差的权重（相对分类误差和置信度误差）。YOLO设置 ${\lambda }_{coord}=5$，即调高位置误差的权
乘以 ${\lambda }_{noobj}$ 调节不存在对象的bounding box的置信度的权重（相对其它误差）。YOLO设置 ${\lambda }_{noobj}=0.5$，即调低不存在对象的bounding box的置信度误差的权重。

四、实验结果

五、结论与思考

作者结论

总结

思考

参考

COCO：AP，AP50，AP70，mAP，AP[.50:.05:.95]什么意思？小白理解
YOLOv3 深入理解
一文看懂YOLO v3
【论文理解】yolov3损失函数