本文主要是介绍《多传感器融合定位》惯性导航基础(一),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
未完待续~:《多传感器融合定位》惯性导航基础(二).
惯性导航基础习题一
- 一、仿真imu数据,并用Allan方差进行分析
- 1.使用gnss-ins-sim进行imu数据仿真
- (1)官方例程demo_allan.py代码解析
- (2)官方例程demo_allan.py运行
- 2.使用imu_utils进行imu数据仿真
- 二、设计一种转台旋转方案,并基于仿真数据进行内参求解的验证
- 1.使用gnss-ins-sim定义标定的运动场景
- 2.使用gnss-ins-sim分立级标定加速度计
- (1)读取仿真文件中的加速度计数据
- (2)分立级解析法标定加速度计实现
- (3)分立级解析法标定加速度计实验对比
- 2.使用gnss-ins-sim分立级标定陀螺仪
- 三、推导基于LM进行加速度计和陀螺仪内参估计的优化过程。按照误差模型,修改参考代码,并基于仿真数据实现。
- 1.使用半系统级(不依赖转台)标定加速度计
- (1)原理及雅克比矩阵的推导
- (2)代码实现加速度计的半系统级标定
- (3)实验对比
- 2.使用半系统级(不依赖转台)标定陀螺仪
一、仿真imu数据,并用Allan方差进行分析
imu数据仿真程序地址: https://github.com/Aceinna/gnss-ins-sim.
Allan方差分析代码地址: https://github.com/gaowenliang/imu_utils.
1.使用gnss-ins-sim进行imu数据仿真
官方提供部分功能的例子程序如表所示:
| 文件名 | 描述 |
|---|---|
| demo_no_algo.py | 一个生成数据的例子,将生成的数据保存到文件并绘制(2D / 3D)感兴趣的数据。没有用户指定的算法. |
| demo_allan.py | 一个陀螺仪和加速度计数据的Allan方差分析演示,并画出的Allan方差的图。 |
| demo_free_integration.py | 一个简单捷联系统的演示。模拟运行1000次。生成了1000个仿真的INS结果的统计信息。 |
| demo_inclinometer_mahony.py | 基于Mahony理论的动态测斜仪算法演示。该演示演示了如何生成感兴趣数据的误差图。 |
| demo_aceinna_vg.py | DMU380动态倾斜算法的演示。该算法首先被编译为共享库。该演示演示了如何调用共享库。这是Aceinna的VG / MTLT产品中的算法。 |
| demo_aceinna_ins.py | DMU380 GNSS / INS融合算法的演示。该算法首先被编译为共享库。该演示演示了如何调用共享库。这是Aceinna的INS产品中的算法。 |
| demo_multiple_algorithms.py | 仿真中的多种算法演示。该演示演示了如何比较多种算法的结果。 |
| demo_gen_data_from_files.py | 该演示演示了如何从记录的数据文件进行仿真。 |
(1)官方例程demo_allan.py代码解析
import os
import math
import numpy as np
from gnss_ins_sim.sim import imu_model
from gnss_ins_sim.sim import ins_sim# globals
D2R = math.pi/180motion_def_path = os.path.abspath('.//demo_motion_def_files//')
fs = 100.0 # IMU sample frequencydef test_allan():'''An Allan analysis demo for Sim.'''#### Customized IMU model parameters, typical for IMU381'''关于imu模型的建立:1.accuracy精度系统定义了三种精度可直接使用 : 'low-accuracy', 'mid-accuracy' , 'high accuracy'.或者如下自定义精度模型:'gyro_b':陀螺仪bias,度/小时'gyro_arw':陀螺角度随机游走,度/ RT-小时'gyro_b_stability':陀螺仪bias不稳定性,度/小时'gyro_b_corr':陀螺仪偏置不稳定性相关性(秒)。将其设置为'inf'以使用随机游走模型将其设置为正实数以使用一阶高斯-马尔可夫模型'accel_b':加速度计bias,米/秒^ 2'accel_vrw':加速度计速度随机游走,米/秒/ RT-小时'accel_b_stability':加速度计bias不稳定性,米/秒^ 2'accel_b_corr':加速度计偏置不稳定性相关性(秒)。'mag_std':磁力噪声STD,UT 2.axis6:仅生成陀螺仪和加速度计数据。9:生成除陀螺仪和加速度计数据外的磁力计数据。3.gpsTrue生成GPS数据,False不生成。'''imu_err = {'gyro_b': np.array([0.0, 0.0, 0.0]),'gyro_arw': np.array([0.25, 0.25, 0.25]) * 1.0,'gyro_b_stability': np.array([3.5, 3.5, 3.5]) * 1.0,'gyro_b_corr': np.array([100.0, 100.0, 100.0]),'accel_b': np.array([0.0e-3, 0.0e-3, 0.0e-3]),'accel_vrw': np.array([0.03119, 0.03009, 0.04779]) * 1.0,'accel_b_stability': np.array([4.29e-5, 5.72e-5, 8.02e-5]) * 1.0,'accel_b_corr': np.array([200.0, 200.0, 200.0]),'mag_std': np.array([0.2, 0.2, 0.2]) * 1.0}# do not generate GPS and magnetometer dataimu = imu_model.IMU(accuracy=imu_err, axis=6, gps=False)#### Allan analysis algorithmfrom demo_algorithms import allan_analysisalgo = allan_analysis.Allan()#### start simulation'''关于Sim的说明:[fs, 0.0, 0.0]:imu(陀螺仪和加速度计),GPS和磁力计的采样频率,此demo中没有后两者motion_def_path+"//motion_def-Allan.csv":初始条件和运动定义,需要指定算法和运动场景。参考ins_sim.py对于Allan方差分析,需要采集的是IMU静止时的传感器数据,因此,运动场景非常简单:保持静止。在完整的运动仿真中,运动场景定义需要包含一系列的运动模式或机动指令。ref_frame:0代表NED坐标系,1代表惯性系mode:车辆操纵能力,[最大加速度,最大角加速度,最大角速度]env:algorithm:算法对象'''sim = ins_sim.Sim([fs, 0.0, 0.0],motion_def_path+"//motion_def-Allan.csv",ref_frame=1,imu=imu,mode=None,env=None,algorithm=algo)'''run():参数为执行次数,默认1results():保存数据,参数为路径,空则不保存plot():画图'''sim.run()# generate simulation results, summary, and save data to filessim.results() # save data files# plot datasim.plot(['ad_accel', 'ad_gyro'])if __name__ == '__main__':test_allan()(2)官方例程demo_allan.py运行


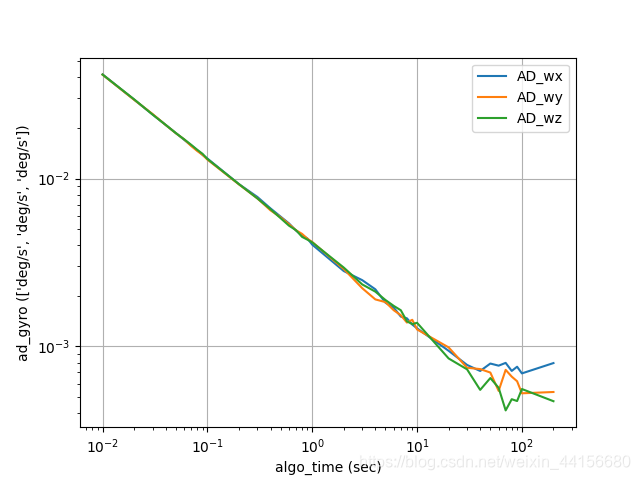
2.使用imu_utils进行imu数据仿真
挖个坑,还没尝试~~
二、设计一种转台旋转方案,并基于仿真数据进行内参求解的验证
1.使用gnss-ins-sim定义标定的运动场景
| Ini lat 经度(deg) | ini lon 纬度(deg) | ini alt 高度(m) | ini vx_body (m/s) | ini vx_body (m/s) | ini vy_body (m/s) | ini vz_body (m/s) | ini pitch (deg) | ini roll (deg) |
|---|---|---|---|---|---|---|---|---|
| command type命令类型 | yaw (deg) | pitch (deg) | roll (deg) | vx_body (m/s) | vy_body (m/s) | vz_body (m/s) | command duration 持续时间(s) | GPS visibilityGPS个数 |
对于其中的命令类型,官方有如下说明:
| Command type | Comment |
|---|---|
| 1 | 直接定义欧拉角变化率和车架速度变化率。变化率在第2〜7栏给出。单位是度/秒和米/秒/秒。第8列给出了该命令将持续多长时间。如果要完全控制每个命令的执行时间,则应始终将运动类型选择为12 |
| 2 | 定义要达到的绝对姿态和绝对速度。目标姿态和速度在第2〜7列中给出。单位是度和m / s。第8列定义了执行命令的最长时间。如果实际执行时间少于最大时间,则将不使用剩余时间,并且将立即执行下一条命令。如果命令不能在最大时间内完成,则在最大时间后将执行下一条命令。 |
| 3 | 定义姿态变化和速度变化。姿态和速度变化在第2〜7列中给出。单位是度和m / s。第8列定义了执行命令的最长时间。 |
| 4 | 定义绝对姿态和速度变化。绝对姿态和速度变化由第2〜7列给出。单位是度和m / s。第8列定义了执行命令的最长时间。 |
| 5 | 定义姿态变化和绝对速度。姿态变化和绝对速度由第2〜7列给出。单位是度和m / s。第8列定义了执行命令的最长时间。 |
对于使用转台的IMU分立级标定而言,至少需要6个不同的转台位置:Z轴朝上,Z轴朝下,X轴朝上,X轴朝下,Y轴朝上,Y轴朝下(定义时多了两个复位)。
根据上述的说明定义转台的运动场景:
在demo_motion_def_files文件夹下定义motion_def_my_imu.csv: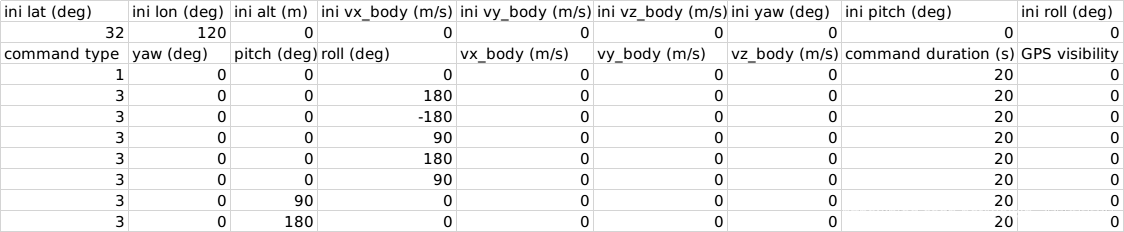
接下来参考demo_allan.py,在gnss-ins-sim文件夹下使用我们刚刚定义的运动模式产生仿真的imu数据,在这里我们要将加速度计三个轴的零偏设置为[0.1,0.2,0.3],具体实现Sim_IMU.py如下:
import numpy as np
import os
import math
from gnss_ins_sim.sim import imu_model
from gnss_ins_sim.sim import ins_sim# globals
D2R = math.pi/180motion_def_path = os.path.abspath('.//demo_motion_def_files//')
fs = 100.0 # IMU sample frequencydef create_sim_imu(): #生成 imu 方针imu数据### Customized IMU model parameters, typical for IMU381imu_err = {'gyro_b': np.array([0.0, 0.0, 0.0]),'gyro_arw': np.array([0.25, 0.25, 0.25]) * 1.0,'gyro_b_stability': np.array([3.5, 3.5, 3.5]) * 1.0,'gyro_b_corr': np.array([100.0, 100.0, 100.0]),'accel_b': np.array([0.1, 0.2, 0.3]),'accel_vrw': np.array([0.03119, 0.03009, 0.04779]) * 1.0,'accel_b_stability': np.array([4.29e-5, 5.72e-5, 8.02e-5]) * 1.0,'accel_b_corr': np.array([200.0, 200.0, 200.0]),'mag_std': np.array([0.2, 0.2, 0.2]) * 1.0}# do not generate GPS and magnetometer dataimu = imu_model.IMU(accuracy=imu_err, axis=6, gps=False)#### start simulationsim = ins_sim.Sim([fs, 0.0, 0.0],motion_def_path+"//motion_def_my_imu.csv",ref_frame=1,imu=imu,mode=None,env=None,algorithm=None)sim.run(1)# generate simulation results, summary, and save data to filessim.results('.//my_sim_imu//') # save data filesif __name__ == '__main__':create_sim_imu()
在进行imu仿真的时候,ins_sim.Sim函数内部会调用acc_gen()函数,该函数在gnss-ins-sim/gnss_ins_sim/pathgen/pathgen.py中定义,在这里函数里可以修改刻度系数和安装误差,修改函数如下:
ks=np.array([[1.02,0.02,-0.03],[0.03,0.96,0.01],[0.04,0.05,1.05]])
ks=np.transpose(ks)
ref_a2=np.dot(ref_a,ks)
a_mea = ref_a2 + acc_bias + acc_bias_drift + acc_noise + acc_vib
修改后产生的加速度数据的内参矩阵为
[ 1.02 0.03 0.04 0.02 0.96 0.05 − 0.03 0.01 1.05 ] \begin{bmatrix} 1.02&0.03 &0.04 \\ 0.02& 0.96 & 0.05\\ -0.03& 0.01 &1.05 \end{bmatrix} ⎣⎡1.020.02−0.030.030.960.010.040.051.05⎦⎤
产生了如下仿真数据:
The following results are saved:time: sample timeref_pos: true position in the local NED frameref_vel: true vel in the NED frameref_att_euler: true attitude (Euler angles, ZYX)ref_accel: true accel in the body frameref_gyro: true angular velocity in the body frameaccel: accel measurementsgyro: gyro measurementsref_att_quat: true attitude (quaternion)
代码采样频率为100hz,每个位置停留20s,即每个位置会产生2000个数据.
2.使用gnss-ins-sim分立级标定加速度计
(1)读取仿真文件中的加速度计数据
在读取的时候遇到了一些问题,我首先打开了文件查看数据格式(默认wps),看起来非常的规范(没有逗号之类的间隔),可是我单个数据读取的时候,莫名其妙的多了很多的间隔,一个数据有些被分成了两个,完全错乱,所以后来改成行读入,按逗号分隔,读入成功.
#include <vector>
#include <Eigen/Core>
#include <iostream>
#include <fstream>
#include <Eigen/Geometry>#define D2R 0.017453292519943295 //角度转弧度bool ReadData(const std::string &path ,std::vector<Eigen::Vector3d ,Eigen::aligned_allocator<Eigen::Vector3d>> &dataVector)
{//清除原有数据dataVector.clear();std::ifstream fin(path);std::string line="";std::string temp="";int cnt=0;while (std::getline(fin,line)){cnt++;if (cnt==1){line="";temp=""; continue;}std::vector<double> acc;for (int i=0;i<line.size();i++){if (line[i]==','){acc.push_back(std::stod(temp));temp="";}else{temp+=line[i];} }acc.push_back(std::stod(temp));line="";temp="";dataVector.push_back(Eigen::Vector3d(acc[0],acc[1],acc[2]));std::cout<<cnt<<": "<<acc[0]<<", "<<acc[1]<<", "<<acc[2]<<std::endl;}if (cnt==0){std::cerr<<"read fail"<<std::endl;return false;}return true;
}
(2)分立级解析法标定加速度计实现
在读取数据的时候我注意到其实数据总共只有15725个(仿真出来的数据也就这么多,不是没有读取到),但是按照推算,8个场景(算上两次复位动作),100hz,20s。那么应该产生16000个数据,显然这存在一些问题.但是我们的标定最少只需要6个不同位置的数据,所以,我们要对这些数据进行一些优化,然后进行标定,代码如下:
void Calibration(std::vector<Eigen::Vector3d ,Eigen::aligned_allocator<Eigen::Vector3d>> &accs)
{Eigen::Vector3d truth_z_down=CalculateMean(accs,1000,1500);Eigen::Vector3d truth_z_up=CalculateMean(accs,3000,3500);Eigen::Vector3d truth_y_down=CalculateMean(accs,7000,7500);Eigen::Vector3d truth_y_up=CalculateMean(accs,9000,9500);Eigen::Vector3d truth_x_up=CalculateMean(accs,13000,13500);Eigen::Vector3d truth_x_down=CalculateMean(accs,15000,15500);
/*std::cout<<"truth_z_up :"<<std::endl;std::cout<<truth_z_up<<std::endl;std::cout<<"truth_z_down :"<<std::endl;std::cout<<truth_z_down<<std::endl;std::cout<<"truth_y_up :"<<std::endl;std::cout<<truth_y_up<<std::endl;std::cout<<"truth_y_down :"<<std::endl;std::cout<<truth_y_down<<std::endl;std::cout<<"truth_x_up :"<<std::endl;std::cout<<truth_x_up<<std::endl;std::cout<<"truth_x_down :"<<std::endl;std::cout<<truth_x_down<<std::endl;
*/Eigen::Vector3d calib_bias;Eigen::Matrix3d calib_sacle_factor;Eigen::Matrix3d calib_installation_error;Eigen::Matrix3d calib_internal_matrix=Eigen::Matrix3d::Identity();//解析法求解 利用6组数据建立六个方程calib_bias=(truth_z_up+truth_z_down)/2;Eigen::Vector3d calib_internal_matrix_col3=(truth_z_up-calib_bias)/g;Eigen::Vector3d calib_internal_matrix_col2=(truth_y_up-calib_bias)/g;Eigen::Vector3d calib_internal_matrix_col1=(truth_x_up-calib_bias)/g;calib_internal_matrix<<calib_internal_matrix_col1[0],calib_internal_matrix_col1[1],calib_internal_matrix_col1[2],calib_internal_matrix_col2[0],calib_internal_matrix_col2[1],calib_internal_matrix_col2[2],calib_internal_matrix_col3[0],calib_internal_matrix_col3[1],calib_internal_matrix_col3[2];calib_internal_matrix.transpose();std::cout<<"calib_internal_matrix: "<<std::endl;std::cout<<calib_internal_matrix<<std::endl;std::cout<<"calib_bias: "<<std::endl;std::cout<<calib_bias<<std::endl;
}int main(int argc ,char** argv)
{//加速度计仿真数据std::string accel_csv_path="./gnss-ins-sim/my_sim_imu/accel-0.csv";std::vector<Eigen::Vector3d ,Eigen::aligned_allocator<Eigen::Vector3d>> accs;ReadData(accel_csv_path,accs);Calibration(accs);
}
(3)分立级解析法标定加速度计实验对比
设定的真实内参矩阵:
[ 1.02 0.03 0.04 0.02 0.96 0.05 − 0.03 0.01 1.05 ] \begin{bmatrix} 1.02&0.03 &0.04 \\ 0.02& 0.96 & 0.05\\ -0.03& 0.01 &1.05 \end{bmatrix} ⎣⎡1.020.02−0.030.030.960.010.040.051.05⎦⎤
设定的真实零飘:
[ 0.1 0.2 0.3 ] \begin{bmatrix} 0.1& \\ 0.2& \\ 0.3& \end{bmatrix} ⎣⎡0.10.20.3⎦⎤
解析法标定的内参模型数据:

2.使用gnss-ins-sim分立级标定陀螺仪
挖坑狂魔,还没做~~~(理直气壮!)
三、推导基于LM进行加速度计和陀螺仪内参估计的优化过程。按照误差模型,修改参考代码,并基于仿真数据实现。
参考框架: https://github.com/Kyle-ak/imu_tk.
1.使用半系统级(不依赖转台)标定加速度计
(1)原理及雅克比矩阵的推导
主要是通过旋转imu到各个位置并在每个位置静止放置一段时间来估计陀螺仪和加速度计的误差.先标定加速度计,再标定陀螺仪。
加速度计标定原理:
取M个静止位置的时候的加速度计均值,该均值经过加速度计零偏,安装误差的补偿后: [ A x A y A z ] = K a ( I + S a ) [ a x a y a z ] + [ ▽ x ▽ y ▽ z ] ≈ ( K a + S a ) [ a x a y a z ] + [ ▽ x ▽ y ▽ z ] \begin{bmatrix} A_{x}\\ A_{y}\\ A_{z} \end{bmatrix} = K_{a}(I+S_{a})\begin{bmatrix} a_{x}\\ a_{y}\\ a_{z} \end{bmatrix} +\begin{bmatrix} \triangledown_{x}\\ \triangledown_{y}\\ \triangledown_{z} \end{bmatrix} \approx (K_{a}+S_{a})\begin{bmatrix} a_{x}\\ a_{y}\\ a_{z} \end{bmatrix} +\begin{bmatrix} \triangledown_{x}\\ \triangledown_{y}\\ \triangledown_{z} \end{bmatrix} ⎣⎡AxAyAz⎦⎤=Ka(I+Sa)⎣⎡axayaz⎦⎤+⎣⎡▽x▽y▽z⎦⎤≈(Ka+Sa)⎣⎡axayaz⎦⎤+⎣⎡▽x▽y▽z⎦⎤其模长为一个重力加速度作为约束。由此来估计出加速度计零偏,安装误差参数,于是有:
f ( θ a c c ) = ∑ k = 1 M ( ∥ [ a x a y a z ] ∥ 2 − ∥ g ∥ 2 ) f(\theta ^{acc})=\sum_{k=1}^{M} \left ( \left \| \begin{bmatrix} a_{x}\\ a_{y}\\ a_{z} \end{bmatrix} \right \|^2 -\left \| g \right \|^2 \right ) f(θacc)=k=1∑M⎝⎜⎛∥∥∥∥∥∥⎣⎡axayaz⎦⎤∥∥∥∥∥∥2−∥g∥2⎠⎟⎞
首先我们通过误差模型,求解出 a ⃗ \vec{a} a:
[ a x a y a z ] = ( I + S a ) − 1 K a − 1 ( [ A x A y A z ] − [ ▽ x ▽ y ▽ z ] ) \begin{bmatrix} a_{x}\\ a_{y}\\ a_{z} \end{bmatrix} = (I+S_{a})^{-1}K_{a}^{-1}\left ( \begin{bmatrix} A_{x}\\ A_{y}\\ A_{z} \end{bmatrix} - \begin{bmatrix} \triangledown_{x}\\ \triangledown_{y}\\ \triangledown_{z} \end{bmatrix} \right ) ⎣⎡axayaz⎦⎤=(I+Sa)−1Ka−1⎝⎛⎣⎡AxAyAz⎦⎤−⎣⎡▽x▽y▽z⎦⎤⎠⎞
在进行IMU坐标轴选定的时候,令:
a.IMU坐标的 X b X_{b} Xb与加速度计的 X a X_{a} Xa重合
b. X b O Y b X_{b}OY_{b} XbOYb与 X a O Y a X_{a}OY_{a} XaOYa共面
所以 S a S_{a} Sa可以化简为:
[ 0 0 0 S a y x 0 0 S a z x S z z y 0 ] \begin{bmatrix} 0 & 0 & 0\\ S_{ayx} & 0 &0 \\ S_{azx}& S_{zzy} & 0 \end{bmatrix} ⎣⎡0SayxSazx00Szzy000⎦⎤
对于一个小量 S a S_{a} Sa而言, ( I + S a ) − 1 ≈ ( I − S a ) (I+S_a)^{-1} \approx (I-S_a) (I+Sa)−1≈(I−Sa),带入化简有:
[ a x a y a z ] = [ 1 0 0 − S a y x 1 0 − S a z x − S z z y 1 ] [ K a x − 1 0 0 0 K a y − 1 0 0 0 K a z − 1 ] ( [ A x A y A z ] − [ ▽ x ▽ y ▽ z ] ) = [ K a x − 1 ( A x − ▽ x ) − S a y x K a x − 1 ( A x − ▽ x ) + K a y − 1 ( A y − ▽ y ) − S a z x K a x − 1 ( A x − ▽ x ) − S a z y K y x − 1 ( A y − ▽ y ) + K a z − 1 ( A z − ▽ z ) ] \begin{bmatrix} a_{x}\\ a_{y}\\ a_{z} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\\ -S_{ayx} & 1 &0 \\ -S_{azx}& -S_{zzy} & 1 \end{bmatrix} \begin{bmatrix} K^{-1}_{ax}& 0 & 0\\ 0 & K^{-1}_{ay} &0 \\ 0&0 & K^{-1}_{az} \end{bmatrix}\left ( \begin{bmatrix} A_{x}\\ A_{y}\\ A_{z} \end{bmatrix} - \begin{bmatrix} \triangledown_{x}\\ \triangledown_{y}\\ \triangledown_{z} \end{bmatrix} \right ) =\begin{bmatrix} K^{-1}_{ax}(A_x-\triangledown_{x})\\ -S_{ayx}K^{-1}_{ax}(A_x-\triangledown_{x})+K^{-1}_{ay}(A_y-\triangledown_{y})\\ -S_{azx}K^{-1}_{ax}(A_x-\triangledown_{x})-S_{azy}K^{-1}_{yx}(A_y-\triangledown_{y})+K^{-1}_{az}(A_z-\triangledown_{z}) \end{bmatrix} ⎣⎡axayaz⎦⎤=⎣⎡1−Sayx−Sazx01−Szzy001⎦⎤⎣⎡Kax−1000Kay−1000Kaz−1⎦⎤⎝⎛⎣⎡AxAyAz⎦⎤−⎣⎡▽x▽y▽z⎦⎤⎠⎞=⎣⎡Kax−1(Ax−▽x)−SayxKax−1(Ax−▽x)+Kay−1(Ay−▽y)−SazxKax−1(Ax−▽x)−SazyKyx−1(Ay−▽y)+Kaz−1(Az−▽z)⎦⎤
求解雅克比矩阵:
∂ f ( θ a c c ) ∂ θ a c c = − ∂ ∥ a ∥ 2 ∂ ∥ a ∥ ⋅ ∂ ∥ a ∥ ∂ a ⋅ ∂ a ∂ θ a c c = − 2 a T ⋅ ∂ a ∂ θ a c c \frac{\partial f(\theta^{acc})}{\partial \theta^{acc}} = -\frac{\partial \left \| a \right \|^2 }{\partial \left \| a \right \|} \cdot \frac{\partial\left \| a \right \| }{\partial a} \cdot \frac{\partial a}{\partial \theta^{acc}}=-2a^T\cdot \frac{\partial a}{\partial \theta^{acc}} ∂θacc∂f(θacc)=−∂∥a∥∂∥a∥2⋅∂a∂∥a∥⋅∂θacc∂a=−2aT⋅∂θacc∂a
所以问题的关键变成了求解 ∂ a ∂ θ a c c \frac{\partial a}{\partial \theta^{acc}} ∂θacc∂a,显然这是一个3*9的矩阵,最后可以得到:
[ 0 0 0 A x − ▽ x 0 0 − K a x − 1 0 0 − K a x − 1 ( A x − ▽ x ) 0 0 − S a y x ( A x − ▽ x ) A y − ▽ y 0 S a y x K a x − 1 − K a y − 1 0 0 − K a x − 1 ( A x − ▽ x ) − K a y − 1 ( A y − ▽ y ) − S a z x ( A x − ▽ x ) − S a z y ( A y − ▽ y ) ( A z − ▽ z ) S a z x K a x − 1 S a z y K a y − 1 − K a z − 1 ] \begin{bmatrix} 0 &0 & 0 & A_x-\triangledown_{x} & 0 & 0 & -K^{-1}_{ax} & 0 &0 \\ -K^{-1}_{ax}(A_x-\triangledown_{x})& 0 & 0 &- S_{ayx}(A_x-\triangledown_{x}) & A_y-\triangledown_{y} & 0 & S_{ayx}K^{-1}_{ax} & -K^{-1}_{ay} & 0 \\ 0&- K^{-1}_{ax}(A_x-\triangledown_{x}) &- K^{-1}_{ay}(A_y-\triangledown_{y}) & -S_{azx}(A_x-\triangledown_{x}) & -S_{azy}(A_y-\triangledown_{y}) & (A_z-\triangledown_{z}) & S_{azx}K^{-1}_{ax} & S_{azy}K^{-1}_{ay} & -K^{-1}_{az} \end{bmatrix} ⎣⎡0−Kax−1(Ax−▽x)000−Kax−1(Ax−▽x)00−Kay−1(Ay−▽y)Ax−▽x−Sayx(Ax−▽x)−Sazx(Ax−▽x)0Ay−▽y−Sazy(Ay−▽y)00(Az−▽z)−Kax−1SayxKax−1SazxKax−10−Kay−1SazyKay−100−Kaz−1⎦⎤
需要注意的是,这里求导的 θ a c c \theta^{acc} θacc并不是 [ S a y x S a z x S a z y K a x K a y K a z ▽ x ▽ y ▽ z ] T \begin{bmatrix} S_{ayx}& S_{azx} & S_{azy}& K_{ax} & K_{ay} & K_{az} & \triangledown_x & \triangledown_y &\triangledown_z \end{bmatrix}^T [SayxSazxSazyKaxKayKaz▽x▽y▽z]T
而是将刻度因子取倒数以后的内参 [ S a y x S a z x S a z y K a x − 1 K a y − 1 K a z − 1 ▽ x ▽ y ▽ z ] T \begin{bmatrix} S_{ayx}& S_{azx} & S_{azy}& K^{-1}_{ax} & K^{-1}_{ay} & K^{-1}_{az} & \triangledown_x & \triangledown_y &\triangledown_z \end{bmatrix}^T [SayxSazxSazyKax−1Kay−1Kaz−1▽x▽y▽z]T
(2)代码实现加速度计的半系统级标定
原代码框架是将 S a S_a Sa的下三角通过IMU坐标的选定设置为0,并使用ceres的自动求导,这里的代码主要是实现手动求解最小二乘问题。
简单回顾一下ceres求导的步骤:
a.定义ceres的最小二乘问题
ceres::Problem problem;
b.向最小二乘问题添加误差项
problem.AddResidualBlock ( cost_function, NULL /* squared loss */, parameter );
ceres::CostFunction* cost_function为误差函数指针,parameter为待估计参数指针。
cost_function的实现有两种方式:
第一种是使用ceres的自动求导,需要构建一个带模板参数的struct,并重载()运算符,在仿函数中实现误差项的定义。此时的cost_function:
cost_function=new ceres::AutoDiffCostFunction< 自定义的误差模型类型, 误差维度, 估计参数维度 > (new 自定义误差模型的匿名对象( 有参构造 ) ) )
第二种是使用手动求导,需要构建一个公共继承自ceres::SizedCostFunction的类,在类中实现虚函数Evaluate,计算雅克比矩阵。
class 自定义计算模型 : public ceres::SizedCostFunction<误差维度,估计维度>
{virtual bool Evaluate(double const* const* parameters,double* residuals,double** jacobians) const {//雅克比的计算}...//省略其他基础的类代码
此时的cost_function:
cost_function=new 自定义计算模型的匿名对象< (有参构造 )
c.配置求解器求解
ceres::Solver::Options options;options.linear_solver_type = ceres::DENSE_QR;//可选QR cholesky等options.minimizer_progress_to_stdout = true;ceres::Solver::Summary summary;ceres::Solve ( options, &problem, &summary );//求解
所以实际上我们所的工作就是修改掉cost_function中原有的赋值,具体的实现如下:
template <typename _T1>
class MultiPosAccResidual_ManualCalculation : public ceres::SizedCostFunction<1,9>
{
public:MultiPosAccResidual_ManualCalculation( const _T1 &g_mag, const Eigen::Matrix< _T1, 3 , 1> &sample ) :g_mag_(g_mag),sample_(sample){}virtual bool Evaluate(double const* const* parameters,double* residuals,double** jacobians) const {Eigen::Matrix< double, 3 , 1> raw_samp( double(sample_(0)), double(sample_(1)), double(sample_(2)) );CalibratedTriad_<double> calib_triad( double(0), double(0), double(0),parameters[0][0], parameters[0][1], parameters[0][2], parameters[0][3], parameters[0][4], parameters[0][5], parameters[0][6], parameters[0][7], parameters[0][8] );Eigen::Matrix< double, 3 , 1> calib_samp = calib_triad.unbiasNormalize( raw_samp );residuals[0] = double ( g_mag_ ) - calib_samp.norm();//雅克比矩阵的计算if (jacobians!=NULL){if(jacobians[0]!=NULL){double Sayx=parameters[0][0];double Sazx=parameters[0][1];double Sazy=parameters[0][2];double Kax=parameters[0][3];double Kay=parameters[0][4];double Kaz=parameters[0][5];double bx=parameters[0][6];double by=parameters[0][7];double bz=parameters[0][8];double Ax=sample_(0);double Ay=sample_(1);double Az=sample_(2);Eigen::Vector3d a(Kax*(Ax-bx),Sayx*Kax*(Ax-bx)+Kay*(Ay-by),Sazx*Kax*(Ax-bx)+Sazy*Kay*(Ay-by)+Kaz*(Az-bz));Eigen::MatrixXd aToTheta(3,9);aToTheta<<0,0,0,(Ax-bx),0,0,-Kax,0,0,Kax*(Ax-bx),0,0,Sayx*Kax*(Ax-bx),(Ay-by),0,-Sayx*Kax,-Kay,0,0,Kax*(Ax-bx),Kay*(Ay-by),Sazx*(Ax-bx),Sazy*(Ay-by),-Sazx*Kax,-Sazy*Kay,-Kaz;//经常会处理其他数据结构和Eigen的转换,//比如把opencv的mat转为eigen的matrix,或者std::vector的填入matrix。//在不进行拷贝的情况下可以使用eigen的map功能进行内存映射。//Eigen::RowMajor 按行优先Eigen::Map<Eigen::Matrix<double, 1, 9, Eigen::RowMajor> > Jacob(jacobians[0]);Jacob.setZero();Jacob=-a.transpose()/a.norm()*aToTheta;}}return true;}
private:const _T1 g_mag_;const Eigen::Matrix< _T1, 3 , 1> sample_;
};
其他修改:
ceres::CostFunction* cost_function =new MultiPosAccResidual_ManualCalculation<_T>(g_mag_, static_samples[i].data());acc_calib_params[0] = init_acc_calib_.misXZ();
acc_calib_params[1] = init_acc_calib_.misXY();
acc_calib_params[2] = init_acc_calib_.misYX();acc_calib_ = CalibratedTriad_<_T>( 0,0,0,min_cost_calib_params[0],min_cost_calib_params[1],min_cost_calib_params[2],min_cost_calib_params[3],min_cost_calib_params[4],min_cost_calib_params[5],min_cost_calib_params[6],min_cost_calib_params[7],min_cost_calib_params[8] );(3)实验对比
原有框架的标定数据:
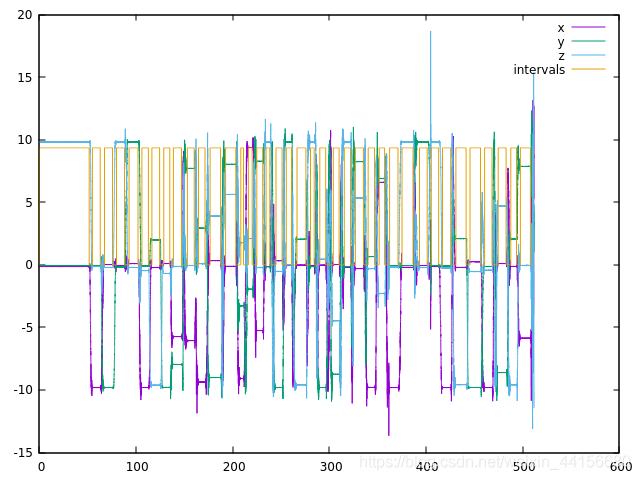
residual 0.13824
Accelerometers calibration: Better calibration obtained using threshold multiplier 6 with residual 0.120131
Misalignment Matrix1 -0.0033593 -0.008906390 1 -0.0213341-0 0 1
Scale Matrix
0.00241278 0 00 0.00242712 00 0 0.00241168
Bias Vector
33124.2
33275.2
32364.4Accelerometers calibration: inverse scale factors:
414.459
412.01
414.649
修改后的标定数据:
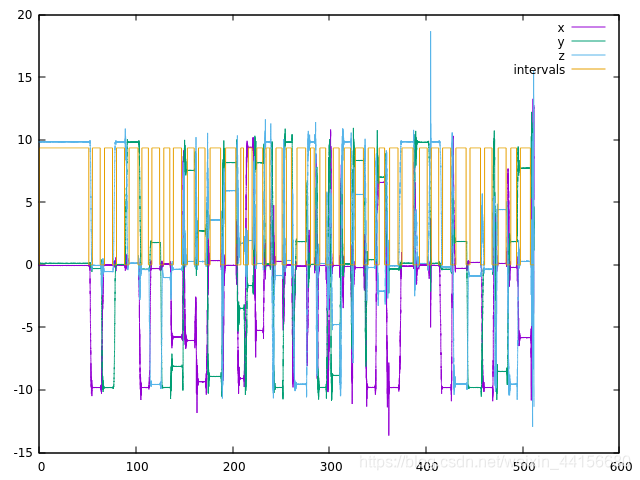
Misalignment Matrix1 -0 00.0246091 1 -0
-0.00897351 0.0348574 1
Scale Matrix
0.00241231 0 00 0.00242669 00 0 0.00241241
Bias Vector
33123.8
33275.4
32364.3Accelerometers calibration: inverse scale factors:
414.54
412.084
414.524
这样对比好像不好检查关于Misalignment Matrix的数值,应该将原框架的改成下三角的自动求导看看数值的~
2.使用半系统级(不依赖转台)标定陀螺仪
下次一定~
这篇关于《多传感器融合定位》惯性导航基础(一)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







