线性代数（二）| 行列式性质 求值 特殊行列式 加边法 归纳法等多种方法

本文主要是介绍线性代数（二）| 行列式性质 求值 特殊行列式 加边法 归纳法等多种方法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

​ 方阵行列式包含着大量的信息

​ 首先它直接告诉我们行列式是否可逆，如果为零则不可逆，如果不为零则可逆

​ 它可

1. 性质

1.1 重要性质梳理

1.1.1 转置和初等变换

1. 对于转置，值不变 |$A^T$|=|$A$|

2. 对于交换行列式的任意两行，行列式值变号

   ​ 可以证明若某两行相同，则行列式值为0

3. 对于某一行（列）乘一个数K，等于给矩阵的行列式乘K

   ​ 注意区别|kA|与 k|A| 其中 $|kA|=k^n|A| $ (A为n阶矩阵）

4. 对于某一行（列）加上另一行（列）的k倍，行列式值不变

1.1.2加法行列式可拆分

​ 行列式的某一行都为两项之和，可以拆分为两行项之和（和的那一行分开，其余行保持不变）。

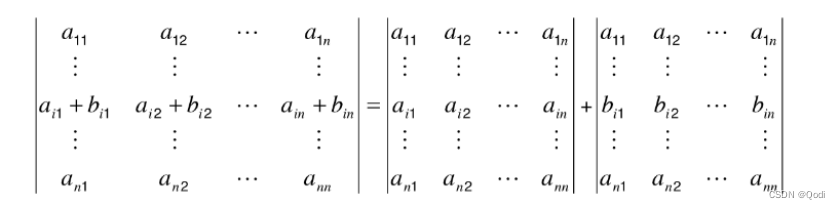
1.1.3 乘积行列式可拆分

设 A B 为n阶方阵，则|AB|=|A||B| 更一般的有|A1A2…As|=|A1||A2|…|As|

1.2 行列式性质的应用

1.2.1 简化运算

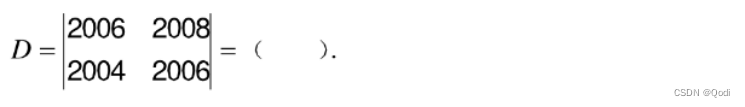
解：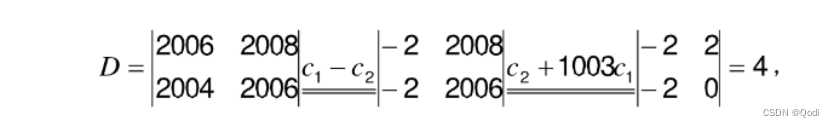

1.2.2 将行列式转换为（二）中的特殊行列式

​ 通过行列式变换转换为特殊行列式

2 特殊行列式

2.1 上三角或下三角行列式

​ 行列式的值为对象线上的元素的乘积，这个可以用行列式的定义来证明，它是一个很重要的行列式，三叉行列式，或者是行列式和为定值的行列式最后本质上都转为了这个特殊行列式

例：

$\left|\begin{array}{ccccc}1& 1& 2& 3& \\ 0& -1& 1& 7& \\ 0& 0& 3& 2& \\ 0& 0& 0& 4& \end{array}\right|=1\times -1\times 3\times 4=-12$

2.2 三叉行列式

​ 本质上需要转换为1 中的上三角或下三角行列式 KP88 1T

​ 例：计算n阶行列式 $\left|\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ -1& 2& 0& \cdots & 0\\ -1& 0& 3& \ddots & ⋮\\ ⋮& ⋮& \ddots & \ddots & 0\\ -1& 0& \cdots & 0& n\end{array}\right|$

​ 解：解决办法就是把主对角线下（上）的元素都变为零，对于本题的话，左下角都为-1,因而可以把第二列乘二分之一加到第一列上去，第三列乘三分之一加到第一列上去……可以得到如下$\left|\begin{array}{ccccc}1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}& 1& 1& \cdots & 1\\ 0& 2& 0& \cdots & 0\\ 0& 0& 3& \ddots & ⋮\\ ⋮& ⋮& \ddots & \ddots & 0\\ 0& 0& \cdots & 0& n\end{array}\right|$

​ 进而采用主对角线上元素相乘即可得到结果 $n!(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n})$

2.3 行列式行和（列和）为定值

如果行和或者列和为定值时，一般采取的方法是将各行（列）加到某一行（列），提取公因式

​ 例：

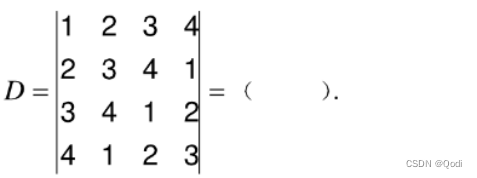
​ 解：

2.4 对称行列式和反对称行列式

​ （1）反对称行列式 主对角线上全为零，主对角上下对应元素相反

​ 如：$\left|\begin{array}{ccc}0& 1& 2\\ -1& 0& 3\\ -2& -3& 0\end{array}\right|$ 反对称行列式有一个重要性质 $A^T=-A$ 基于这一性质，我们可以推出若反对称行列式为奇数阶 ，则行列式值为零，左面这个行列式即为零 ，证明 因为$A^T=-A$ 所以$|A^T|=|-A|=（-1{）}^n|A|$ 当n为奇数，则有 $|A^T|=-|A|$ 又因为转置行列式值不变 ，所以$|A|=-|A|$ 则|A|只能为0

​ （2）对称行列式 主对角线上元素无要求，主对角上下对应元素相等

​ 如：$\left|\begin{array}{ccc}1& 1& 2\\ 1& 2& 3\\ 2& 3& 0\end{array}\right|$

2.5 范德蒙行列式

​ 范德蒙行列式

3.求行列式值的基本方法

3.1 行列式定义

​ 用行列式定义求的矩阵具有较多的零元素的特征，相应元素取过之后所在列所在行就不能再取元素了

​ 例1 求A=$\left|\begin{array}{ccccc}1& 1& 0& 0& \\ 2& -1& 0& 0& \\ 0& 0& 3& 0& \\ 0& 0& 4& 4& \end{array}\right|$

​ 解： A=1×(-1)×3×4+（-1）×1×2×3×4=-36

拓展C P9 1T 3T

3.2 行列式性质

​ 利用（一）中的行列式性质，如加法行列式可拆性，基本变换等结合一些行列式两行成比例结果为零的一些推论

​ 例2 求A=$\left|\begin{array}{cccc}{a}^2& (a+1{)}^2& (a+2{)}^2& (a+3{)}^2\\ b^2& (b+1{)}^2& (b+2{)}^2& (b+3{)}^2\\ c^2& (c+1{)}^2& (c+2{)}^2& (c+3{)}^2\\ d^2& (d+1{)}^2& (d+2{)}^2& (d+3{)}^2\end{array}\right|$

​ 解：$\left|\begin{array}{cccc}{a}^2& (a+1{)}^2& (a+2{)}^2& (a+3{)}^2\\ b^2& (b+1{)}^2& (b+2{)}^2& (b+3{)}^2\\ c^2& (c+1{)}^2& (c+2{)}^2& (c+3{)}^2\\ d^2& (d+1{)}^2& (d+2{)}^2& (d+3{)}^2\end{array}\right|$=$\left|\begin{array}{cccc}{a}^2& a^2+2a+1& a^2+4a+4& a^2+6a+9\\ b^2& b^2+2b+1& b^2+4b+4& b^2+6b+9\\ c^2& c^2+2c+1& c^2+4c+4& c^2+6c+9\\ d^2& d^2+2d+1& d^2+4d+4& d^2+6d+9\end{array}\right|$

​ 将右边完全拆开后，一共有3×3×3=27种组合相加，但每种组合总会有成比例的两列，因而最后行列式=0

3.3 行列式的展开

行列式的展开本质是降阶，是一种非常重要的方法，降阶的话有可以得到二阶三阶行列式方便计算，或者是我们可以得到一种递推关系式（n阶矩阵）

（1）如 $\left|\begin{array}{ccccc}1& 1& 3& 0& \\ 2& -1& 1& 0& \\ 5& 6& 3& 0& \\ 1& 2& 4& 4& \end{array}\right|$可按最后一列展开，则可以直接降解为三阶行列式，我们发现某一行（列）的零越多越好，多一个零就少算一个行列式。

有时候某一列的零不是很多，但是我们又没有其他好的方法计算，我们可以先进行一些变换，使得某一列或某一行的零变多，进而简化运算，如要求$\left|\begin{array}{ccccc}1& 1& 3& 1& \\ 2& -1& 1& 2& \\ 5& 6& 3& 3& \\ 1& 2& 4& 4& \end{array}\right|$ 我们可以先用第二行减去二倍的第一行，第三行减去三倍的第一行，第四行减去四倍的第一行，得到$\left|\begin{array}{ccccc}1& 1& 3& 1& \\ 0& -3& -5& 0& \\ 2& 3& -6& 0& \\ -3& -2& -8& 0& \end{array}\right|$按最后一列展开即可降阶为三阶**-**$\left|\begin{array}{cccc}0& -3& -5& \\ 2& 3& -6& \\ -3& -2& -8& \end{array}\right|$记得前面的负号不要丢掉，再按第一列展开即可得到两个二阶行列式

（2）对于n阶矩阵，我们不可能降阶到二阶三阶，但是我们可以找到递推关系式进而求出答案

3.4 加边法

​ 基于行列式展开让行列式升阶

3.5 归纳法

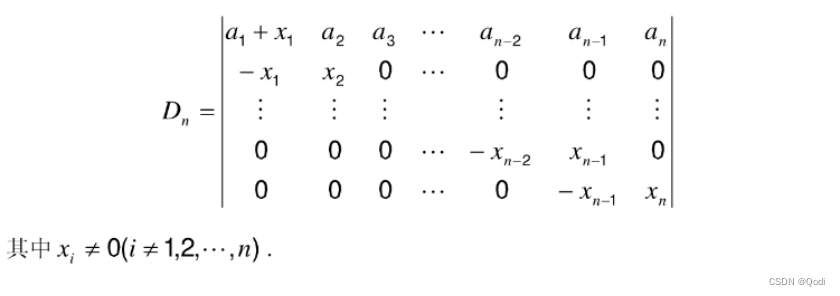
​ 解：

这篇关于线性代数（二）| 行列式性质 求值 特殊行列式 加边法 归纳法等多种方法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---