归纳法专题
算法笔记03--归纳法之生成排列
生成排列 生成排列即对n个数的全排列,显然时间复杂度是n指数级的O(n^k) 假定可以生成n-1个数的所有排列,那么就可以扩展生成1,2,.....,n的排列。 例如1的生成排列即1 1,2的生成排列即1,2和2,1 1,2,3的生成排列在1,2的生成排列基础上可以这样得到: 1在第1位,2,3的生成排列 2在第1位,1,3的生成排列 3在第1位,2,3的生成排列 那么推广到1,
算法笔记02--归纳法之多项式求值(Horner规则)
多项式求值 假设有n+2个实数a0,a1,...,an和x的序列,求多项式 p_nx = a_nx^n + a_n-1x^n-1 + ...+ a_1x + a_0; 则需要乘法:n+n-1 + ...+2+1 = n(n+1)/2 需要加法:n 可见算法效率为O(n^2) 而p_nx = ((...((((a_n)x + a_n-1)x + a_n-2)x + a_n-3)....)
算法笔记01--归纳法之整数幂
整数幂 算法1:对实数x的n次幂设计一个有效的算法。一种直接的方法是对x用迭代方法自乘n次,这种方法十分低效,因为它需要O(n)乘法。一个高效的方法可以用如下方法推出,令m=n/2,假设已经知道如何计算x^m。那么有两种情况:如果n是偶数,那么x^n = (x^m)^2;否则x^n = x(x^m)^2。 算法2:令n的二进制表示为dn-1.....d1,d0。从y=1开始,由n的高位至地位扫
【PL理论深化】(3) MI 归纳法:归纳假设 (IH) | 结构归纳法 | 归纳假设的证明
💬 写在前面:所有编程语言都是通过归纳法定义的。因此,虽然编程语言本身是有限的,但用该语言编写的程序数量是没有限制的,本章将学习编程语言研究中最基本的归纳法。本章我们继续讲解归纳法,介绍归纳假设和结构性归纳法。 目录 0x00 归纳假设 (IH) 和结构归纳法 0x01 归纳假设的证明 0x00 归纳假设 (IH) 和结构归纳法 归纳法是一种用于证明归纳定义的集合中的元素所具有
逻辑推理:归纳法和演绎法
归纳法和演绎法是两种不同的推理方法,用于从已有的信息推导出结论。以下是它们的区别和举例说明: 归纳法 (Inductive Reasoning) 归纳法是从具体的实例出发,经过观察和分析,得出一般性结论的一种推理方法。这种方法的结论具有概率性,而不是绝对确定的。 特点: 从具体到一般。结论具有一定的不确定性。需要大量实例作为基础。 例子: 假设你观察到以下情况: 天鹅A
【数学归纳法 反证法】菲蜀定理
裴蜀定理(或贝祖定理,Bézout’s identity)得名于法国数学家艾蒂安·裴蜀,说明了对任何整数a、b和它们的最大公约 数d,关于未知数x和y的线性不定方程(称为裴蜀等式):若a,b是整数,且(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立。 它的一个重要推论是:a,b互质的充要条件是存在整数x,y使ax+by=1.
数学经典思想:数学归纳法 理解+实战
导语: “数学归纳法”大家应该听起来并不陌生,从初中到大学应该都有使用这种思想去解题的经历。只不过在不同阶段的学习中难度不同,理解程度不同。最近在做一些高数方面相关的练习的时候用到的蛮多的,所以今天拎出来在自我学习巩固的过程中也可以和大家分享讨论。 1.定义 数学归纳法(Mathematical Induction, MI)是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然
约瑟夫环问题-基础版(数学归纳法)
问题:n个人围成一圈,从1开始报数,报到m的人死,然后后面的人接着报数。。。直到最后剩下一个人,求最后这个人的初始编号是多少 可以根据游戏进程进行正向模拟,但是我觉得这种方式是最自然的思考模式,肯定不是最优算法。 实际上:确实不是最优。 更优的算法是根据结果进行倒推: 首先为所有人编号: 初始号:0 1 2 3 4 5
【AcWing】蓝桥杯集训每日一题Day10|递归|暴力|数学归纳法|1360.有序分数(C++)
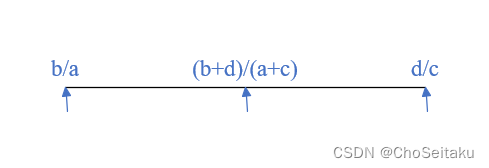
1360.有序分数 1360. 有序分数 - AcWing题库难度:简单时/空限制:1s / 64MB总通过数:4128总尝试数:6630来源:usaco training 2.1算法标签枚举排序最大公约数递归Stern-Brocot Tree 题目内容 给定一个整数 N,请你求出所有分母小于或等于 N,大小在 [0,1] 范围内的最简分数,并按从小到大顺序依次输出。 例如,当 N=5
人工智能数学验证工具LEAN4【入门介绍9】高级乘法世界:逆否策略的等效替代,提取假设 的已知,tauto另类理解,更 严格的归纳法假设。。。
视频讲解:人工智能数学验证工具LEAN4【入门介绍9】高级乘法世界:逆否策略的等效替代,提取假设 的已知,tauto另类理解,更 严格的归纳法假设。。。_哔哩哔哩_bilibili import Game.Levels.AdvMultiplication.L08mul_eq_zero World "AdvMultiplication" Level 9 Title "mul_left_can
an+1=an+2*an+1 的归纳法证明通项公式
习题来源:《基础数论》[(美)杜德利 著] 译者:周仲良 附录一:习题7 题: 假定,且对n=1,2,…,有,用归纳法证明: 这里先解出通项公式的推导过程,然后再证明通项公式的n的范围 解1: 由变形:知:为首项为2,公比为2的等比数列: 列出各项: 。 解2: 。 归纳法证明通项的正确性,晚上写。。
《线性代数:行列式》:数学归纳法
一、第一类数学归纳法 (1) 验证 n=1 时,命题成立 (2) 假设 n=k 时,命题成立 (3) 证明 n=k+1 时,命题成立 则命题对任意正整数 n 成立 二、第二类数学归纳法 (1) 验证 n=1 和 n=2 时,命题成立 (2) 假设 n<k 时,命题成立 (3) 证明 n=k 时,命题成立 则命题对任意正整数 n 成立
线性代数(二)| 行列式性质 求值 特殊行列式 加边法 归纳法等多种方法
文章目录 1. 性质1.1 重要性质梳理1.1.1 转置和初等变换1.1.2加法行列式可拆分1.1.3 乘积行列式可拆分 1.2 行列式性质的应用1.2.1 简化运算1.2.2 将行列式转换为(二)中的特殊行列式 2 特殊行列式2.1 上三角或下三角行列式2.2 三叉行列式2.3 行列式行和(列和)为定值2.4 对称行列式和反对称行列式2.5 范德蒙行列式 3.求行列式值的基本方法3.1
C++归纳法解决动物繁殖问题算法
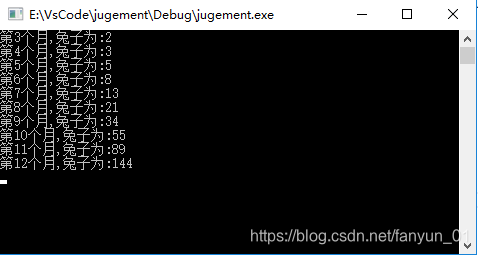
1.有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月,后每个月又生一对兔子,假如兔子都不死,问每个月的兔子总数为多少? 2.实现原理 先推算前几步,然后自己分析一个规律,再验证这个规律,其实就是归纳法,分析完之后,发现兔子的继承关系和最右侧的兔子总数,符合斐波那契数列规律。 3.代码实现如下 #include "stdafx.h"#include<stdi