2020年数维杯数学建模B题以家庭为单位的小规模多品种绿色农畜产品经营模式开发求解全过程文档及程序

2020年数维杯数学建模

B题 以家庭为单位的小规模多品种绿色农畜产品经营模式开发

原题再现：

  在全球化疫情蔓延和国民生活水平稳步提高大形势下，居民对于绿色农畜产品的需求可能会迎来新的爆发期。传统大规模种植或养殖模式因其较大的风险、产品质量的非保障性及难以解决大规模居民就业问题等方面的缺陷将逐步丧失竞争优势。另外，国家所提倡的乡村振兴策略及解决各地区发展不充分不协调的问题的迫切需求等均预示着以家庭为单位或小规模的个性化种植与养殖计划有望成为国家新一轮的经济增长点。这种模式较为适合我国这一具有庞大人口规模及城镇化比率较高的国家加以推广。未来农村牧区的经营模式将会逐步走向两个极端，一类是大规模的种植与养殖模式，而另一类是较小规模的精细化和绿色化的生产模式。

  请您利用数学建模的方法为以家庭为单位的广大具有种植或养殖计划的农牧民提供合理化的养殖计划，其具体问题包括：

  问题1：请您通过网络平台搜集适合不同地区种植的农产品（包括粮食、蔬菜及水果等）产量及价格相关时间序列数据，并对不同农产品预期的人力成本及收入展开相关分析讨论；

  问题2：请为具有充足土地资源的农民们提供合理的大规模农产品种植计划，这一计划不仅能够保障农民们的稳定收入，同时也能最大限度的保证土地资源的循环利用；

  问题3：针对缺乏土地资源的农民们提供合理的小规模种植计划，这一计划能够兼顾农民基本收入的同时尽量减少水资源的过度使用；

  问题4：如果在农业基础之上同时考虑牧业与渔业相关经营，您能否提出更为合理的种植与养殖计划；

  问题5：一个家庭经营多种农畜产品往往消耗过多的人力成本，您能否提供一个几个家庭合作后的最优养殖计划。

整体求解过程概述(摘要)

  本文首先分析了不同地区种植农产品的产量及相关数据，得到其变化趋势并建立农产品预期的人力成本和价格模型；其次，对土地资源充足和缺乏的地区提供合理种植方式，保证土地资源的充分利用及水资源合理使用；最后，在农业基础上考虑多种产业间的合理配合，提供更为合理的种植与养殖计划以及多家庭合作计划。
  针对问题一，通过中国农村统计年鉴以及查阅文献搜集了辽宁、山东、河北省种植玉米、小麦、苹果等农作物的产量、价格、人力成本的相关时间序列数据。首先，根据价格与产量随时间变化的数据绘制图像并分析得出三个省份所耕种的不同农作物随着时间的增长其产量及价格都呈现上升的趋势；其次，利用线性拟合的方法建立了的人工成本与价格之间的数学模型并利用最小二乘法对数学模型进行求解；最后，通过建模方程可知辽宁省种植玉米以及山东省种植苹果的收入在未来的一段时间内仍可以保持持续升高的收入，而河北省种植小麦的收入将有略微的下降。
  针对问题二，所提出的为具有充足土地资源的农民们提供合理的大规模农产品种植计划，使得所提出的计划既能够保障农民们的稳定收入，同时也能最大限度的保证土地资源的循环利用的问题。在具有充足土地资源的条件下，对农产品生产计划决策问题建立网络模型，并进行了算例分析
  针对问题三，根据土地生产特性构建农产品生产计划的数学模型，由于数学模型变量（农产品）在选择与生产上具有时间特性，故而引入网络分析法，将数学模型转化为网络计划图的多方案评价问题，运用动态规划逆解法对整合优化后的网络图进行对比，从而制定农产品最优生产计。并进行了算例分析。
  针对问题四，我们在农业基础之上同时考虑养殖经营，采用根关联流率基本入树建模法，建立系统反馈分析模型。生成可循环的农畜经营图，采用极小模反馈传递分析法，给出反馈环开发管理对策，提出规模养种一体的种植与养殖循环农业发展计划。
  针对问题五，我们构建了针对农户的成本收益函数的数学模型，定性的分析农户饲养规模对其成本收益的影响，在此基础上，定量求解二次型规划，同时采用数值模拟得出最优养殖计划结论：农户规模在其能力范围内，规模越大越容易获得与企业合作机会，饲养品质越好，抗风险能力越高，我们大致估算出几个农户投入的资产等于企业外部投入资产与农户饲养边界变动成本的一半。

问题分析：

  对于问题一：主要在于收集不同地区种植农产品的产量，价格，人力成本等方面的数据，并且在此基础上要建立人力成本及收入之间相关性的数学模型。首先，题中未给定地区以及种植农产品的名称，因此需要通过查阅文献以及相关统计网站对不同地区种植农产品的产量，价格，人力成本等数据进行搜索；其次，需要根据搜集来的数据，做出相关折线图或散点图，对不同数据之间的关系进行分析，得出不同变量之间的相关性或变化趋势；最后，应选择合适的数学建模方法对人力成本及收入之间相关性进行建模，通过对数学模型的求解以得出题目所要求的答案。
  对于问题二：首先根据农产品生产的时空特性和农产品生产时间柔性引入网络流规划构建网络模型；通过网络流量平衡分析，推导网络模型应满足的约束条件，结合各农产品的定量化控制，对大规模农产品生产网络模型进行线性优化；再进一步考虑农产品生产率的影响因素，构建非线性约束和目标函数对线性模型进行扩展；最后通过具体实例诠释大规模农产品生产计划拟订过程。结果表明，土地满负荷生产农产品将打破市场的供需平衡，容易造成“丰产不丰收”现象；利用本文模型制定农产品生产计划，虽土地有闲置，但在土地闲置期间，土地肥力能得到恢复，各种有机质能得到再生，有利于为农产品持续生产提供良好的生产条件和环境，有利于提高农产品的质量和产量，增加经济效益。
  对于问题三：针对缺乏土地资源的农民们提供合理的小规模种植计划，满足农民基本收入的同时尽量减少水资源的过度使用，对于有跨越年度的农产品生产网络已经没有跨年度的生产网络应用线性规划解决现实问题遵循抽象现实问题—建立模型—求解模型—分析结果的步骤。抽象现实问题是线性规划模型建立的关键，主要内容是把现实问题抽象为线性方程和线性函数；并转变为线性规划问题，从而能借助数学方法求解。本文凭借大规模农产品生产网络抽象现实问题，并演绎大规模农产品生产的目标函数和约束条件，满足线性规划求解的条件。
  对于问题四：问题 4 参考查阅相关文献，针对农业和牧业养殖业的特点，分析当下生产过程中的问题提出采用根关联流率基本入树建模法，建立系统反馈分析模型。生成可循环的农畜经营图，采用极小模反馈传递分析法，给出反馈环开发管理对策，提供规模养种一体的循环农业发展计划。
  对于问题五：问题 5 针对一个家庭经营多种农畜产品往往消耗过多的人力成本的现实问题，同时现阶段家庭养殖小而分散、抗风险能力低下的特点，我们构建了针对农户的成本收益函数的数学模型，定性的分析农户饲养规模对其成本收益的影响，在此基础上，定量求解二次型规划，目的是为提供一个几个家庭合作后的最优养殖计划，改变目前一个家庭经营多种农畜带来的小、弱、散的面貌。

模型假设：

  假设 1：本文中所提供的数据真实可靠。
  假设 2：对于人力成本与及每亩土地产出的价格之间的相关性不与其他外界因素（如天气，水分，作物成活率等方面）有关。
  假设 3：对于人力成本与及每亩土地产出的价格之间的相关性不与其他外界因素有关
  假设 4：针对问题二与问题三的土地资源规模，有足够多的劳动力去完成农产品种植任务。
  假设 5：针对问题二与问题三，假设所种植的农产品都具有相对稳定的市场环境

模型的建立与求解

数据的预处理：

  我们搜集了辽宁省、河北省、山东省三个省份不同农产品的产量及价格相关的数据，经过整理所得的数据如附录中表 5-1-1、5-1-2、5-1-3 所示。
  表 5-1-1、5-1-2、5-1-3 分别给出了不同地区种植农产品的产量及价格相关的时间数据。其中，农作物每亩的价格包含了在生产过程中劳动力，所投入的资金总量，以及该地区种植农作物所需的土地成本。表 5-1-1、5-1-2、5-1-3 中以每亩物质与服务费用、每亩人工成本和每亩土地成本的形式给出数据，通过分析这些数据可以决定农户种植该农作物的收入利益成本，另一方面也是导致农户是否会选择种植这种农作物的重要原因。为了更加清楚的分析不同农作物时间、产量、价格之间的关系，图 5-1-1 给出了不同时间下产量与价格之间的变化曲线。

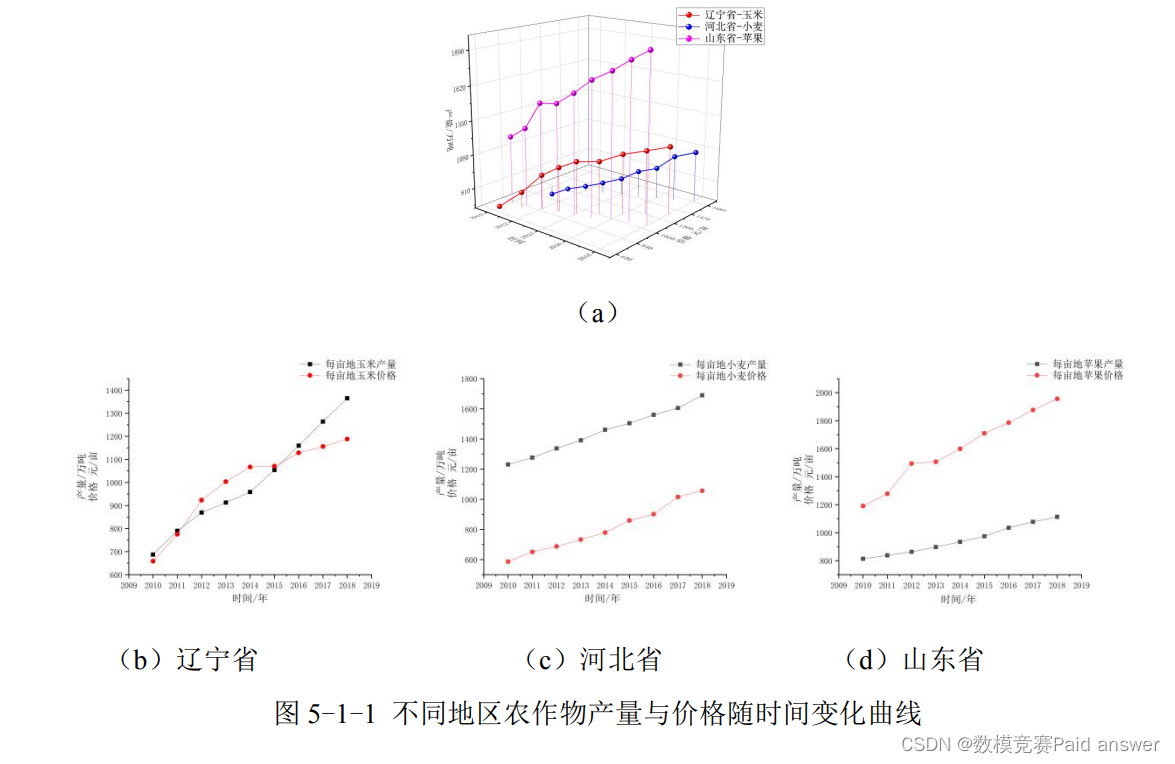
  图 5-1-1（a）综合时间、产量、价格三方面因素给出了三者之间的总体变化三维折线图。其中，三个不同省份所耕种的农作物其产量及价格随时间的增长基本呈现上升趋势，但在不同年限内农作物的产量和价值上升幅度略有不同。
  图 5-1-1（b）、（c）、（d）将时间与各地区农作物的产量和价格关系变得更为清楚。从不同省份种植农作物的产量及生产价格走势来看，其总体上都是保持增长的趋势。但价格随时间变动的情况要比产量随时间变动的情况表现的更为复杂，曲线变化较大。产生这种现象的原因是价格的高低除了与单位面积成本有关，还受到单位面积产量的影响，根据农业生产的特点，自然条件（如气候、光热、降水、土壤等）对农业生产的影响效果十分显著，在不同年份之间相同农产品的产量有可能出现较大波动，因此也就造成了价格在不同年间变化情况的多样性和复杂性。
  农产品人力成本及价格之间关系模型的建立
  由表 5-1-1、5-1-2、5-1-3 中价格变化可知，不同农产品每亩地的人工成本在2010-2018 年间涨幅最高，对价格的影响最大。因此，对于人工成本以及价格之间的关系还需要进一步的分析。由于本文只对人工成本与价格进行分析，因此结合上述表 5-1-1、5-1-2、5-1-3 中数据，可以选择曲线拟合的方法分析人工成本与价格的关系，在大多数的工程实践中，我们将已知的数据近似的拟合成一个经验公式，用以分析和预期反映变量之间的关系，称为回归分析。

农产品人力成本及收入模型的求解

  根据上述已建立的价格与人工成本间的方程，以及表 5-1-1、5-1-2、5-1-3 中已知数据，利用 MATLAB 软件进行仿真（源程序见附录中程序一）得到了拟合曲线的非线性拟合曲线及经验公式如图 5-1-2 所示。


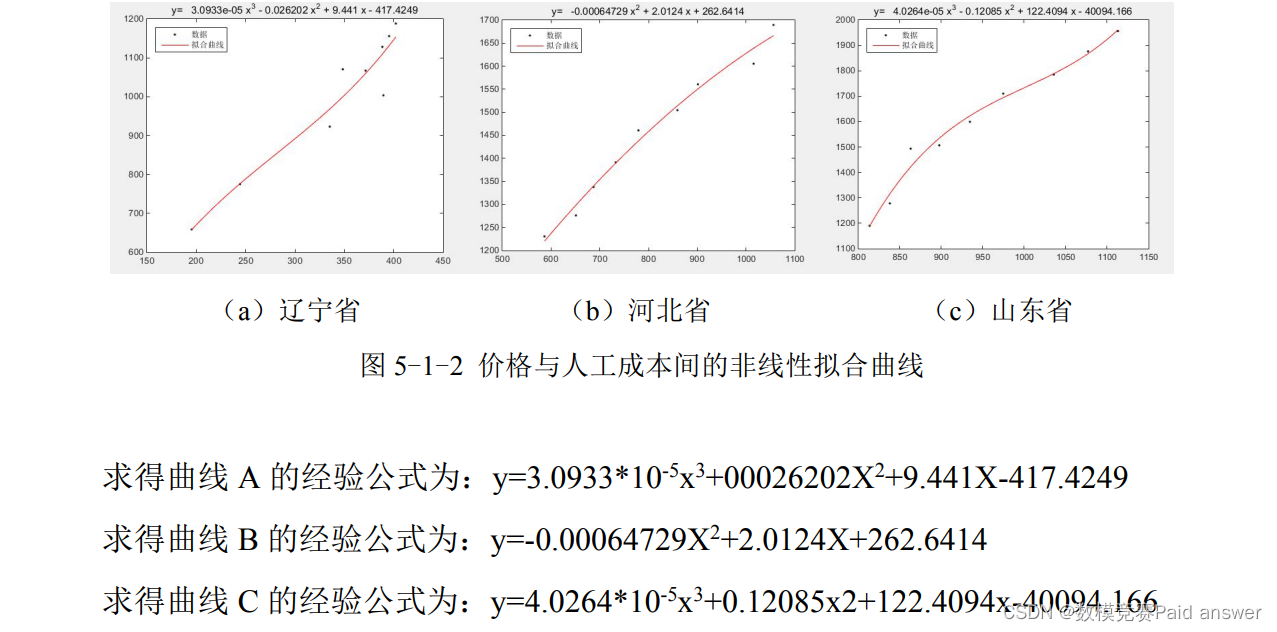
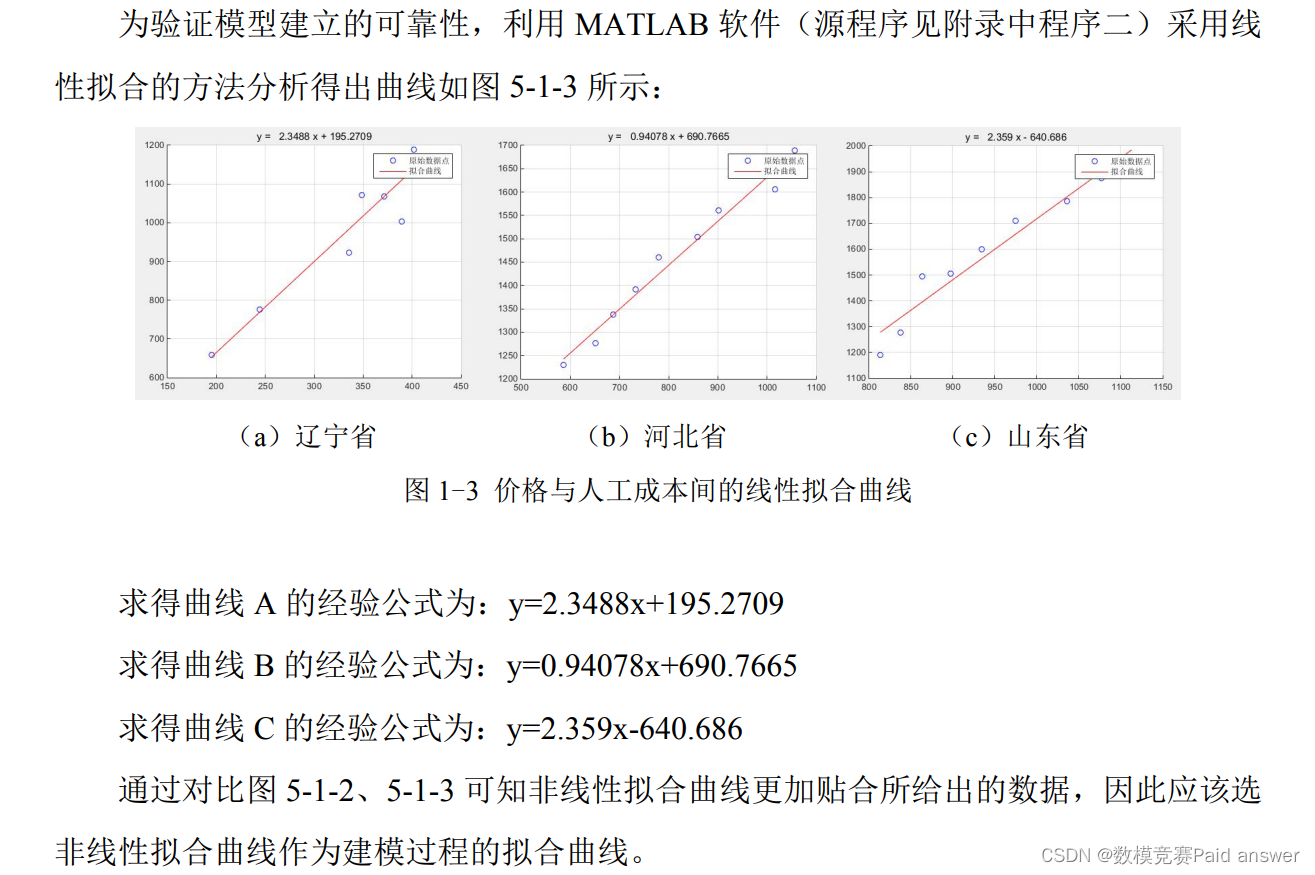
  随着人工成本的增加，辽宁省种植玉米以及山东省种植苹果的价格将呈现一个增长的趋势，该趋势表明农产品逐年增长的价值利润将高于人工成本的增长，在未来的一段时间内仍可以保持持续升高的收入；而河北省种植小麦逐年增长的利润将低于人工成本的增长，农产品总体价值较往年有所升高，但是在未来的一段时间内的净收入将有略微的下降。

大规模农产品时间柔性种植计划模型的建立

基于时空约束的大规模农产品时间柔性生产网络模型

  本文以辽宁省A地作为大规模生产种植的算例进行分析建模。以辽宁省种植成本以及种植的净利润为基础，根据 A 地的实际情况确定种植时间（具体建模参数见附录中表5-2-1）既保证农民生产收入又保证土地资源的合理利用得到大规模农产品种植计划（分析所得的具体种植计划安排见附录中表 5-2-2）

基于时空约束的中小规模农产品生产计划动态优化模型的建立

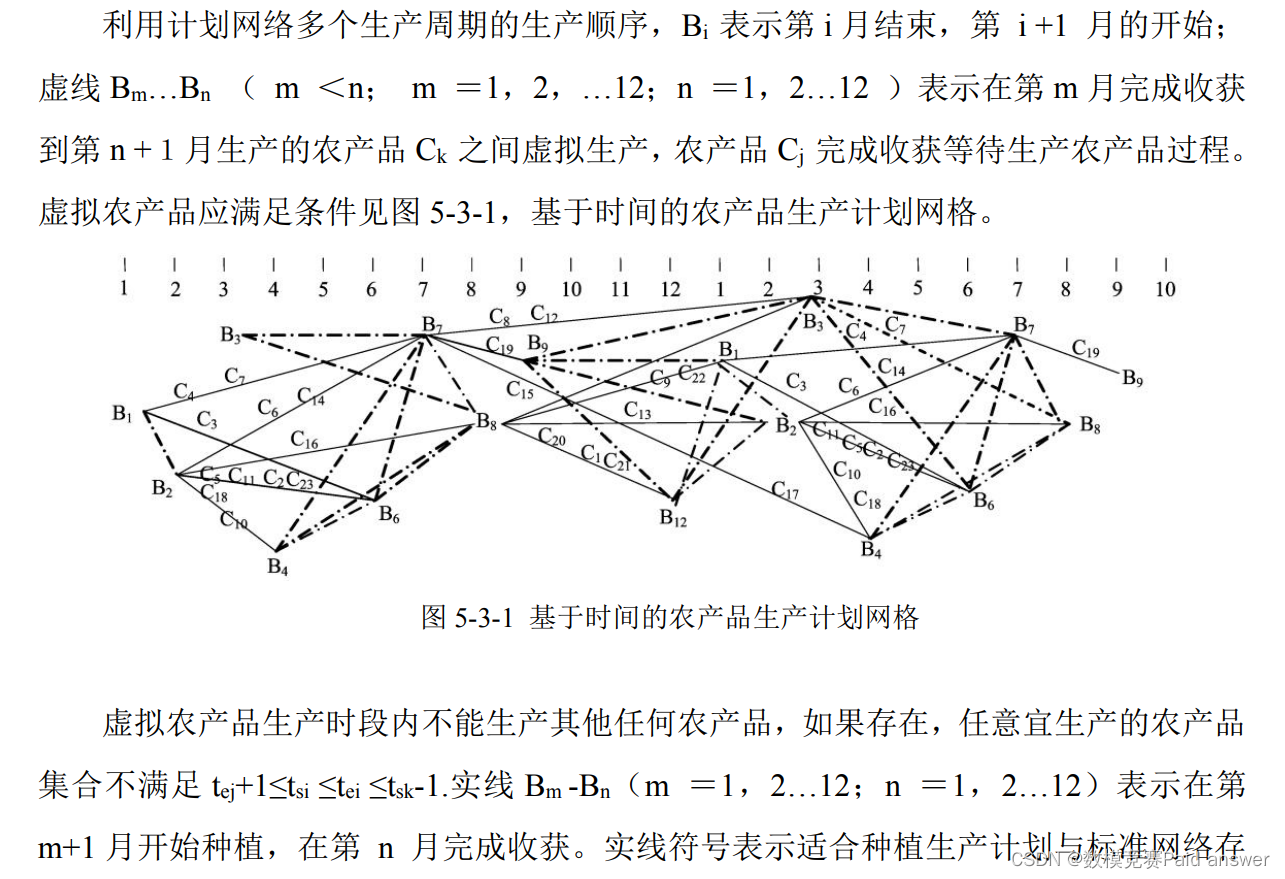
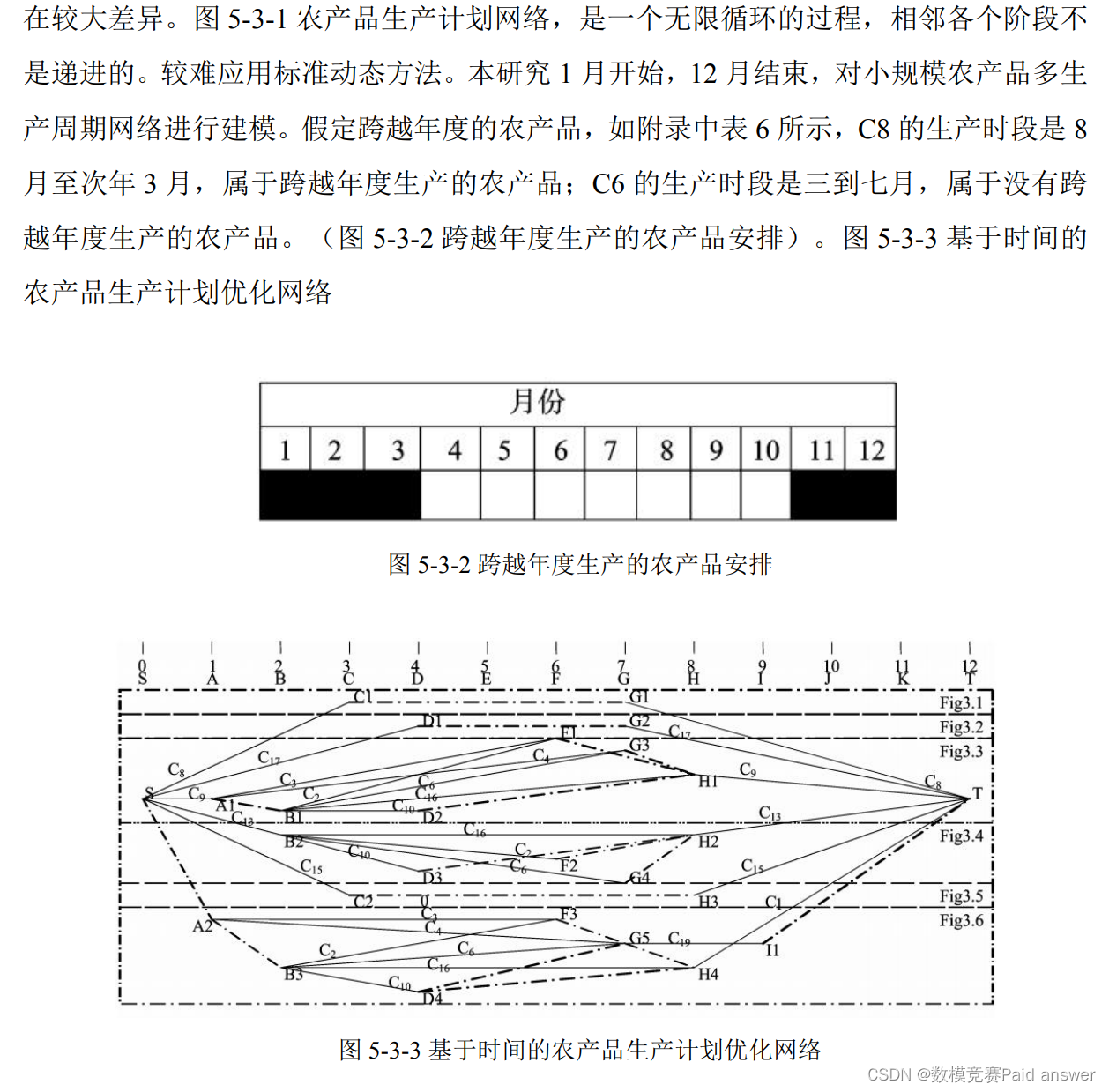
  本问题以辽宁省 B 地小规模农产品种植为研究计划。兼顾 B 地区家庭小规模种植的经济收入，并考虑水资源等必要因素，依托第一部分所提到的模型以及计算方法，对于家庭为单位的小规模种植进行了种植计划的研究，并且通过国家数据库调查辽宁省B地农产品生产时间（附录中表 5-3-1）。以 一年作为小规模农产品生产计划周期，拟定的生产计划。


  根据国家统计局数据得到小规模农产品净利润受到土地资源限制、水资源限制的扰动，应引入实时数据修正小规模农产品生产计划优化网络。如果某农产品不适应小规模种植条件，就不进行种植。本研究确定了农产品生产时段的准确性，农产品的生产时段直接影响后续农产品对于水资源需求的影响，并且还通过准确的数据确定了净利润的准确性。

种养结合循环农业数据的预处理：

  我们小组参考相关研究文献，种养结合循环农业污染第三方治理系统是以沼气工程为纽带联接养殖业与种植业，污染第三方治理是核心。养殖业、污染治理企业、种植业的利润是系统发展的动力，养殖规模、沼气工程规模、种植业规模是系统发展的保障。
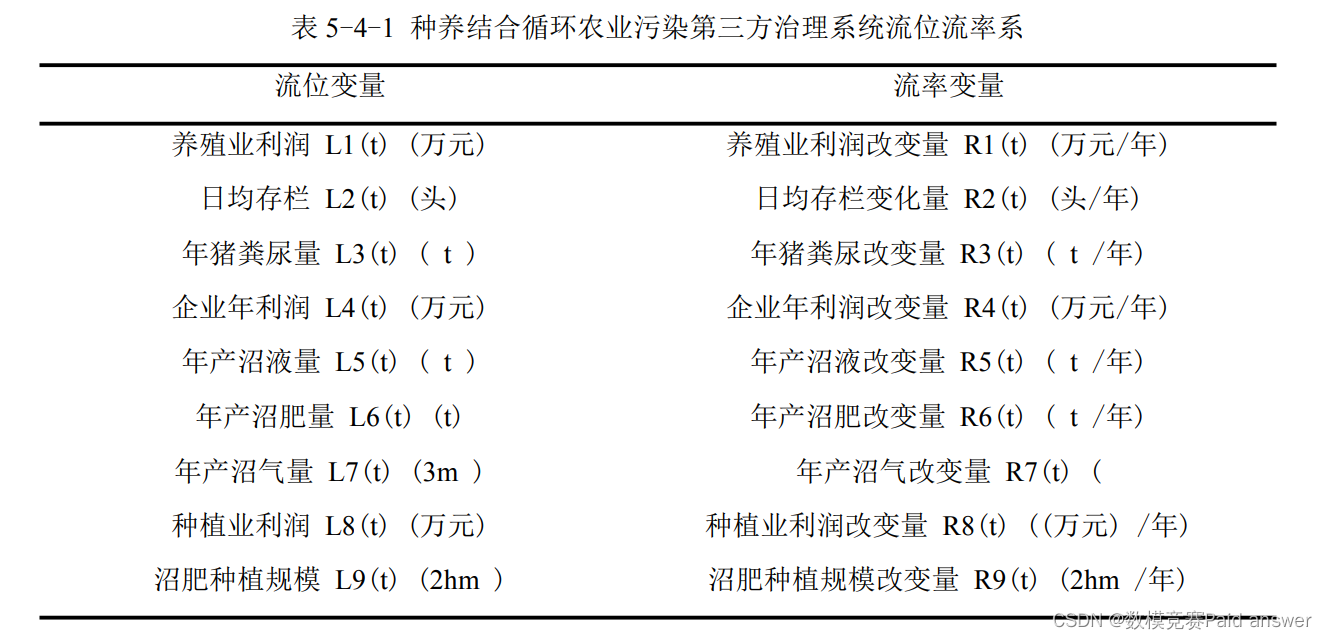
  基于专家判断力，确定养殖业利润、企业年利润、种植业利润、日均存栏、年产沼液量、沼肥种植规模为流位变量； 基于循环经济理论，循环经济以“再循环、再使用、减量化”为原则。再结合实践，污染第三方治理的实践体现了循环经济的“再循环”原则，即废弃物再次资源化。系统中的废弃物为猪粪尿，废弃物资源化产品为沼气能源和沼肥资源。基于理论、实践，确定年猪粪尿量、年产沼气量、年产沼肥量为系统的流位变量。综上，确定如下种养结合循环农业污染第三方治理系统结构的九组流位、流率系，如表 5-4-1 所示。

种养结合循环农业模型的建立

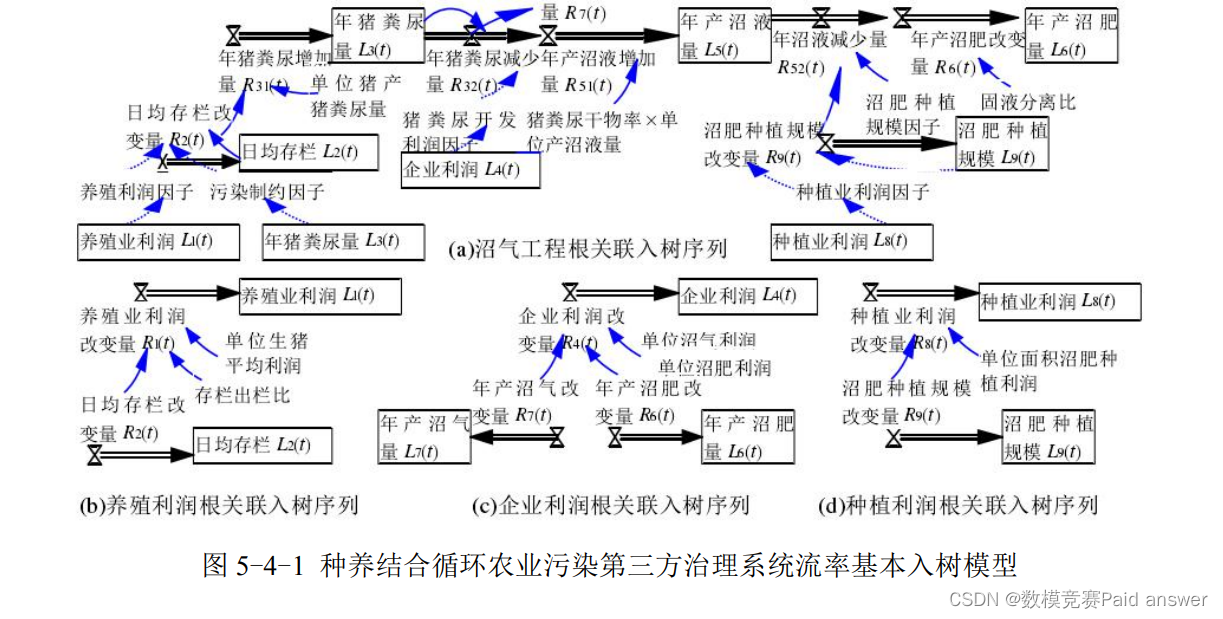
  建立种养结合循环农业污染第三方治理系统流率基本入树模型：建立三个刻画沼气工程的序列模型，得到刻画沼气工程物理流程的序列模型如图 5-4-1：a 所示；同时建立两个刻画企业利润的序列模型，再逐一建立其他序列模型，得到刻画系统利润目标的序列模型如图 5-4-1：b～d 所示。进而，得到种养结合循环农业污染第三方治理系统流率基本入树模型如图 5-4-1：

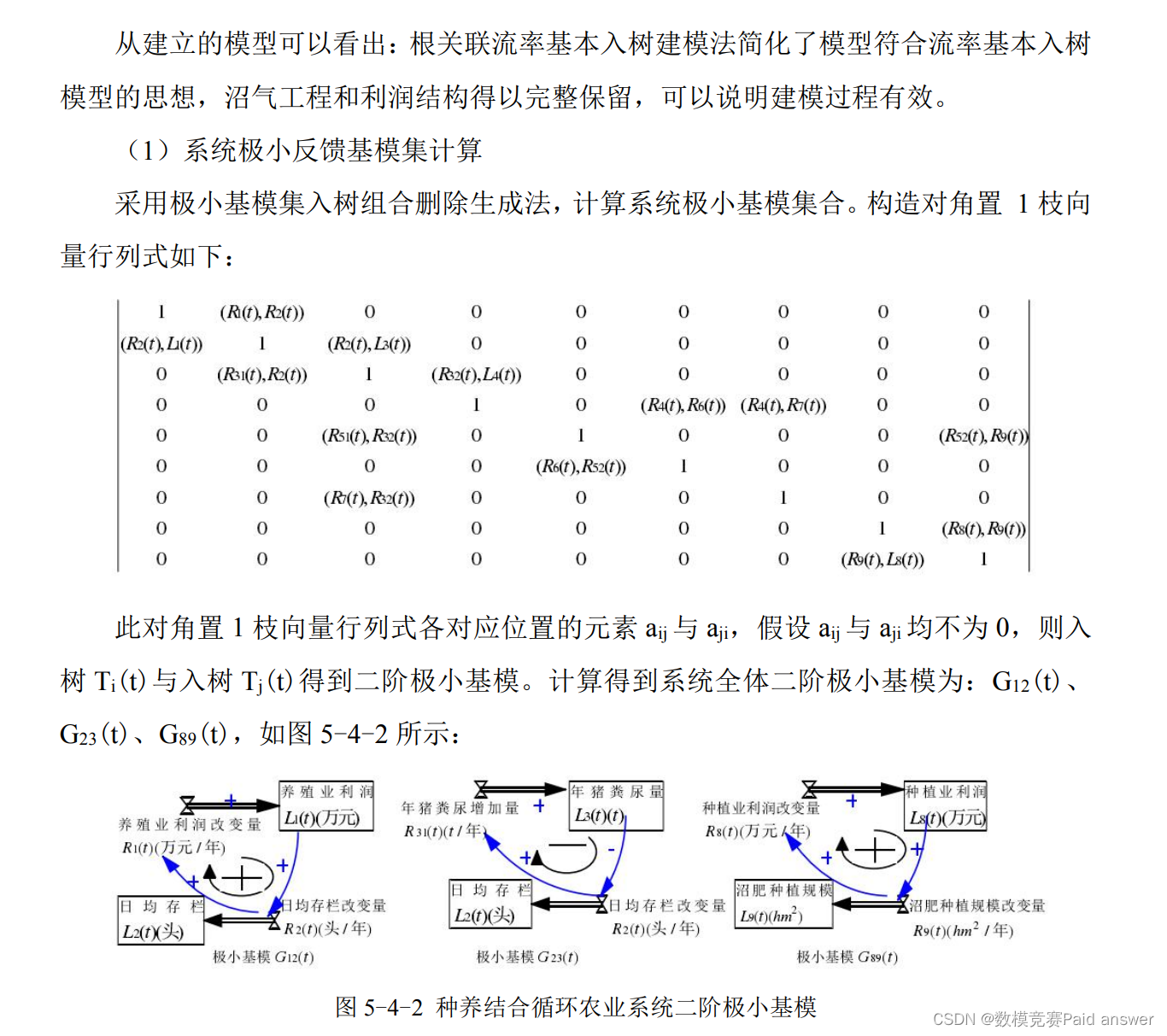
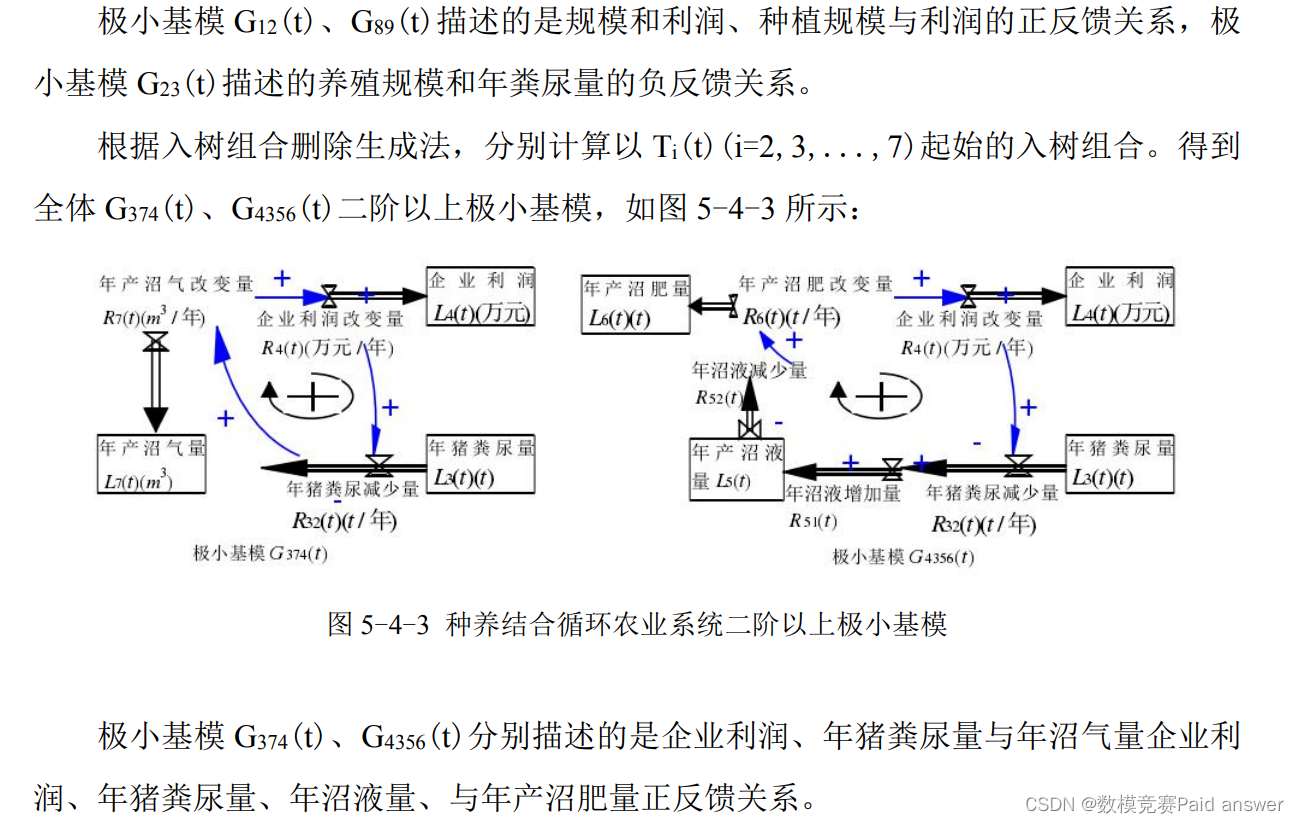
系统反馈环开发管理对策结果分析

  1.建立专业化、规模化养殖；健全养殖主体环保责任制度、废弃物资源化考核制度，建立受益者付费机制。
  2.加强财税政策支持污染治理项目，沼气发电按特许价销售，企业开发环保技术，提升污染治理能力和效率。
  3.研究绿色有机农产品，施用有机肥增加土壤肥力，增加有机沼肥的需求，提高农产品的产量与品质。

最优养殖计划数据的预处理：

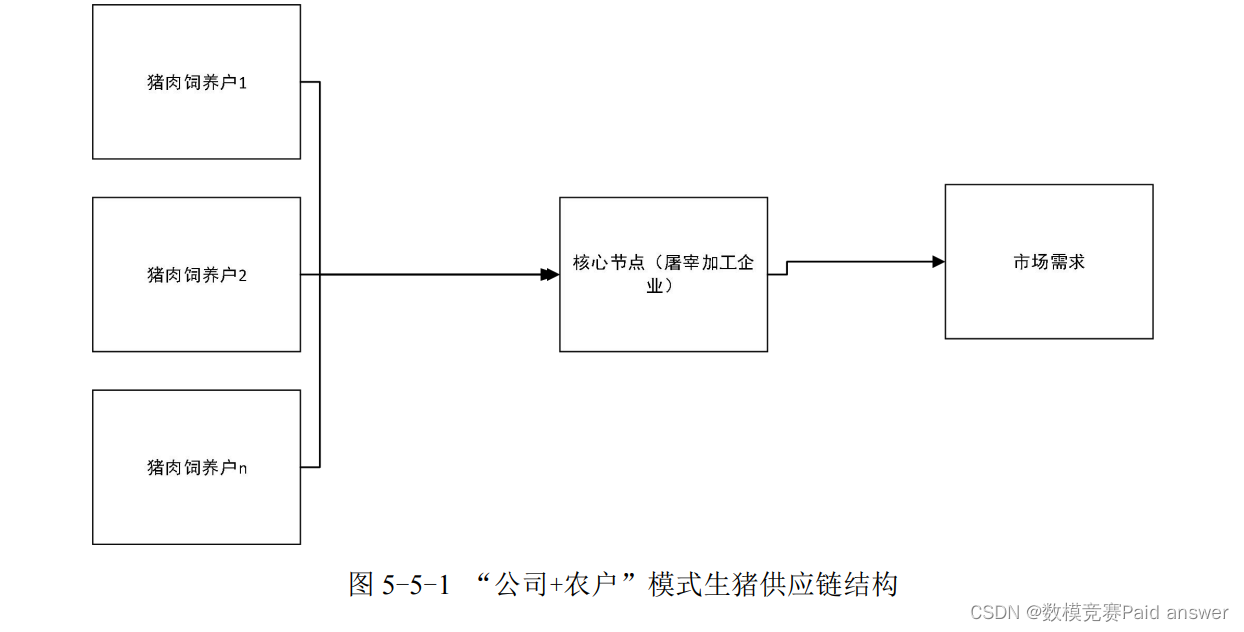
最优养殖计划模型的建立

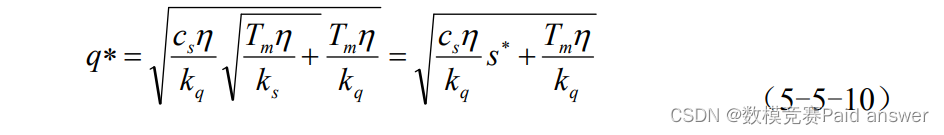
最优养殖计划结果分析

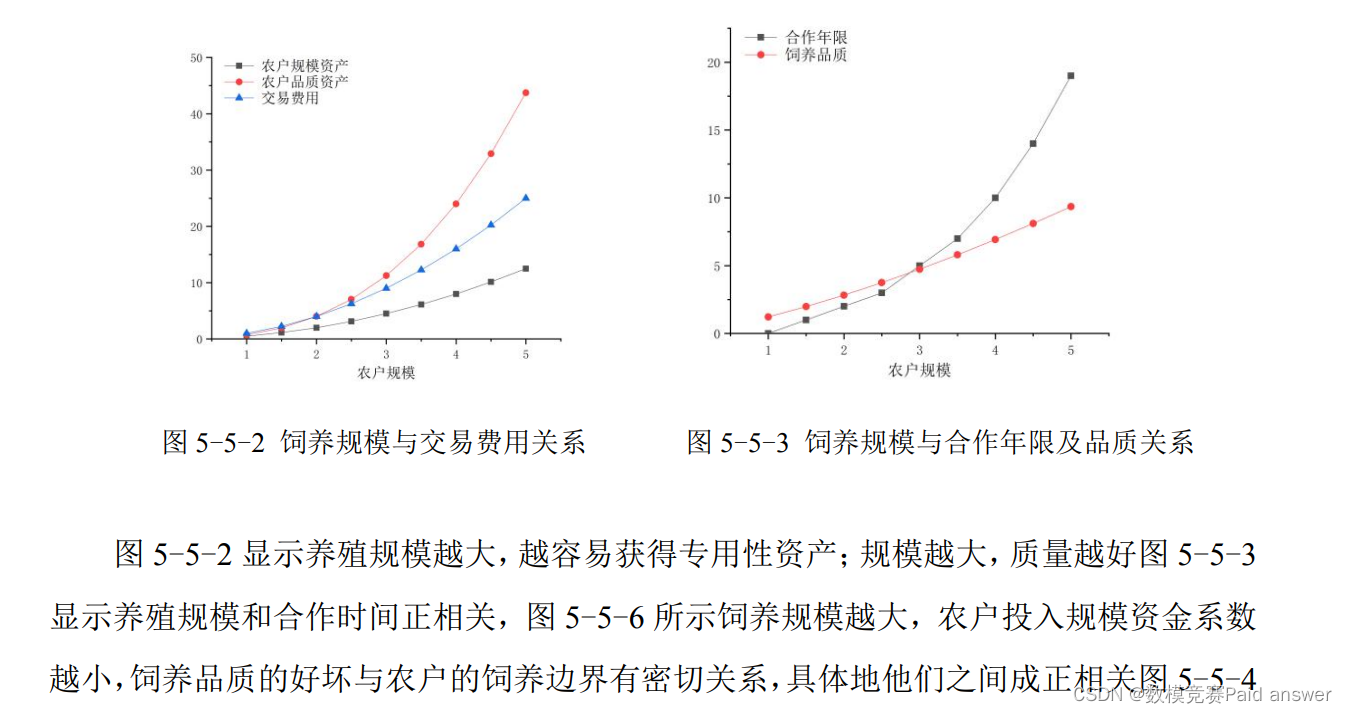
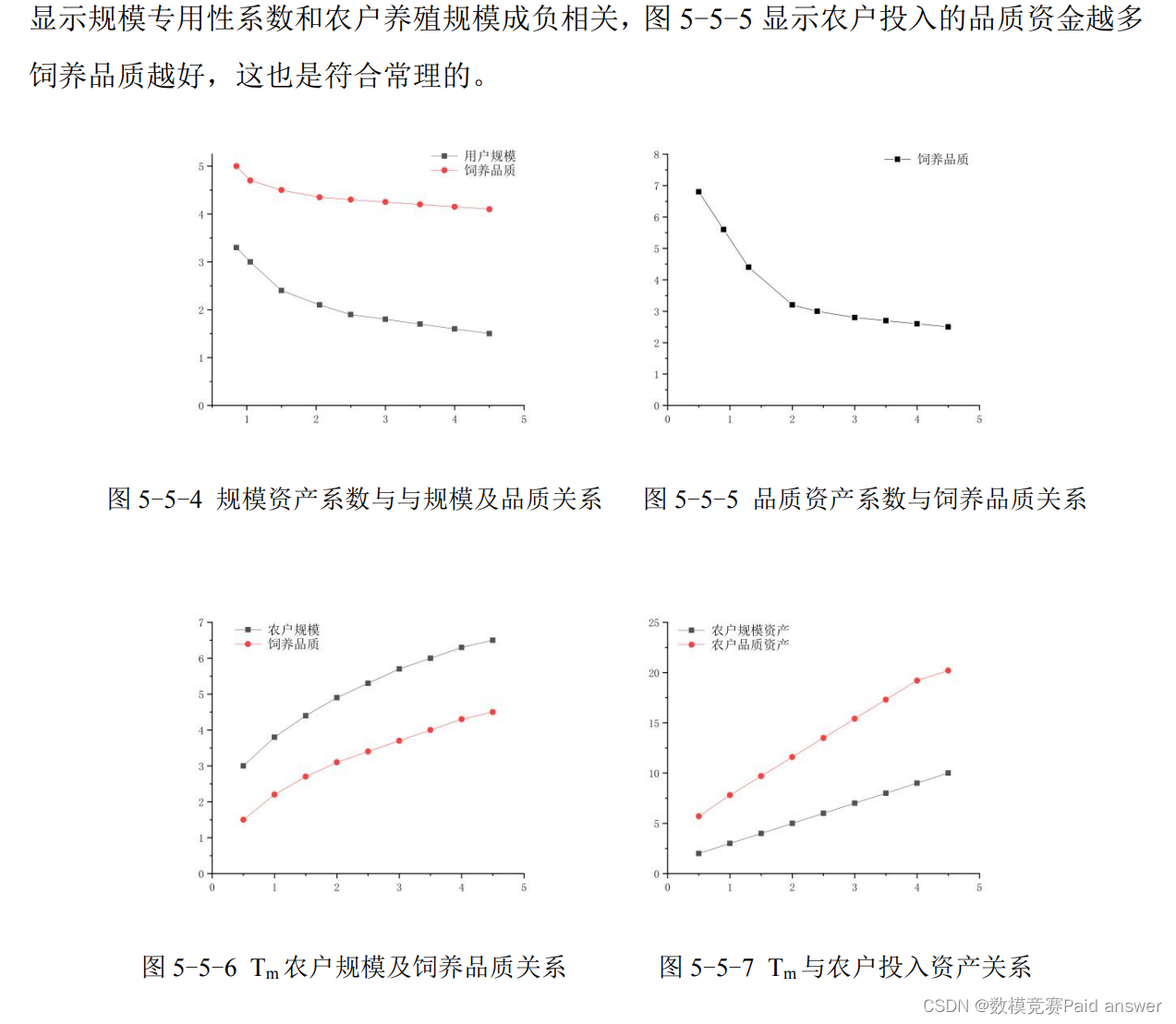
  通过以上分析可以提出一些家庭农户养殖计划的建议：
  站在家庭养殖农户的角度，如果由于各种原因导致饲养规模较小，那么势必会导致各方向其投入的规模性资金较少，与之相关的企业也不愿意与其签订长期的合作协定，缺乏相关的技术服务，饲养品质自然无法得到保障。但是，农户可以自由的选择饲养领域，发挥自己的主观能动性。
  通过建模分析可以发现农户与企业合作的时间长短、饲养品质都与饲养规模有很强的相关性。合作时间越长家庭饲养品质越好，经济效益自然也就越好，饲养规模越倾向于扩大。同时，饲养规模扩企业就更愿意与饲养农户长期合作。这样就形成了一个良性的闭环循环。使得产业链健康发展，各方均能获得利益。
  综合分析提出建议：
  单个家庭劳动力较少，家庭合作扩大养殖规模，就容易获得与企业长期合作的机会，规避单个家庭小而散的养殖风险，同时也可以建立一条长期的产业供应链，使得各方面都有稳定地收入，饲养品质提高有利于消费者。建立与企业合作的规模化养殖，解可以有效地解决肉类价格波动带来的风险问题。研究发现要扩大规模，就得从投入栏舍、及养殖配套设备相应资产发力，这样有利于吸引技术、人才进入，进而提高饲养品质，健康产业发展。

论文缩略图：

程序代码：

非线性曲线拟合程序

clear;
clc;
x=[813.492;837.9;863.03;897.55;934.46;974.66;1035.6;1077.024;1113.05];%辽宁省种植玉米
的人工成本
%x=[586.48;651.036;687.39;732.74;779.4;859.4;901.42;1015.72;1056.46]河北省种植小麦的人
工成本
%x=[813.492;837.9;863.03;897.55;934.46;974.66;1035.6;1077.024;1113.05]山东省种植苹果的
人工成本
y=[1189.91;1278.04;1493.7;1506.57;1599.26;1710.19;1785.5;1876.23;1956.26];%辽宁省种植
玉米的价格
%y=[1230.6;1276.1;1337.7;1391.2;1460.7;1504.5;1560.7;1605.4;1689.5]河北省种植小麦的价
格
%y=[1189.91;1278.04;1493.7;1506.57;1599.26;1710.19;1785.5;1876.23;1956.26]山东省种植苹
果的价格
n=1;
%%曲线拟合
p=polyfit(x,y,n);
r=sum(sqrt((y-polyval(p,x)).^2));
TF=1;
while(TF)
nnew=n+1;
pnew=polyfit(x,y,nnew);
rnew=sum(sqrt((y-polyval(pnew,x)).^2));
if rnew>=r
break;
end
n=nnew;p=pnew;r=rnew;
end
xx=linspace(min(x),max(x));
plot(x,y,'k.');hold on
plot(xx,polyval(p,xx),'r');
hold off;
%%作图
title(['y=' poly2str(p,'x')]);
legend('数据','拟合曲线','location','northwest');
程序二：线性曲线拟合
clc;
clear;
%%引入数据
x = [195.4;244.4;335.29;389.63;371.6;348.5;388.6;395.4;402.2];
%x=[586.48;651.036;687.39;732.74;779.4;859.4;901.42;1015.72;1056.46]%河北省种植小麦的
人工成本
%x=[813.492;837.9;863.03;897.55;934.46;974.66;1035.6;1077.024;1113.05]%山东省种植苹果
的人工成本
y = [658.56;775.22;923.05;1003.5;1067.12;1070.6;1128.34;1155.83;1188.38];
%y=[1230.6;1276.1;1337.7;1391.2;1460.7;1504.5;1560.7;1605.4;1689.5]%河北省种植小麦的价
格
%y=[1189.91;1278.04;1493.7;1506.57;1599.26;1710.19;1785.5;1876.23;1956.26]%山东省种植
苹果的价格
%%曲线拟合
p = polyfit(x,y,1);
xx = min(x):.1:max(x);
yy = polyval(p,xx);
f = poly2str(p,'x');
hold on;
%%作图
plot(x,y,'bo');
plot(xx,yy,'r-');
legend('原始数据点','拟合曲线');
title(['y =' f]);
grid on;
hold of；