本文主要是介绍关于涉及频谱分辨率的一些问题以及FFT幅度谱数值矫正问题的梳理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题
在研究matlab的FFT函数的时候发现了如下问题:对于信号
y = e j 2 π f 1 t + e j 2 π f 2 t + e j 2 π f 3 t y=e^{j2\pi f_1t}+e^{j2\pi f_2t}+e^{j2\pi f_3t} y=ej2πf1t+ej2πf2t+ej2πf3t
其中 f 1 = 500 H z f_1=500Hz f1=500Hz, f 2 = 505 H z f_2=505Hz f2=505Hz, f 2 = 1010 H z f_2=1010Hz f2=1010Hz。当我用 F s = 5120 H z F_s=5120Hz Fs=5120Hz的采样率对其进行采样得到512个离散数据点,画出其频谱为:

问题一:频谱本应该是在500Hz、505Hz和1010Hz三处有峰,但是频谱上却没有显示出505Hz的信号。
问题二:由时域表达式可知,三个不同频点的信号功率一致,都为1。但是幅度谱上却无体现。
频谱分辨率、栅栏效应及频谱泄露
在简介栅栏效应之前,我们要分清DTFT、DFT和FFT三者的关系,可以参考我的这篇文章。
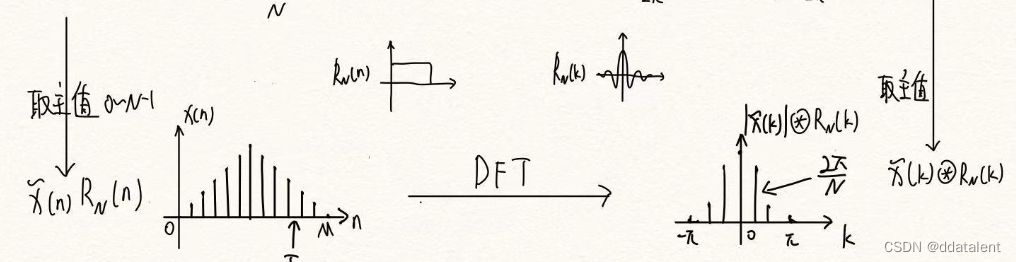
我们不妨细看DFT这个步骤,我们在matlab里调用FFT就是采用的DFT算法(当FFT点数是2的整数次幂的时候,就可以用快速傅里叶变换)。
频谱分辨率
由上图可知,我们最终得到的时域信号是以采样周期 T = 1 F s T=\frac{1}{Fs} T=Fs1为间隔,频谱中的谱线以 2 π N \frac{2\pi}{N} N2π间隔,这就是我们的频谱分辨率。
转换到数字上则有: Δ f = F s N \Delta f=\frac{Fs}{N} Δf=NFs,在本例中则是 Δ f = 5120 512 = 10 H z \Delta f=\frac{5120}{512}=10Hz Δf=5125120=10Hz。
栅栏效应
我们可以想象,间隔10Hz的谱线,应该是会跳过我们的505Hz这个频点的信号。就好像通过栅栏观察频谱一样,因此叫做栅栏效应。
那么难道我们就观察不到这个频点的信号了吗?如果我们漏掉了505Hz这个频点的信号,那我们500Hz和1010Hz两个频点的信号功率不应该是一致的吗,怎么会幅度不一样呢?
频谱泄露
由上图可知,DFT的最后一个步骤是加窗,将一个无限长的信号截断为有限长的信号。在频域上,就是卷积一个Sa函数。

Sa函数的特性是能量集中在主瓣,少部分能量分布在旁瓣。这样原本各个频点的冲激信号经过卷积变为了Sa函数,能量也从集中分布在某个频点变为大部分集中,小部分泄露的情况。这就是我们说的频谱泄露。
回归到这个例子中,505Hz频点处的信号能量集中分布在505Hz附近的主瓣中,少部分泄露到其他地方去了。可是505Hz谱线最后由于频谱分辨率的原因并没有被采集到,而500Hz的谱线不仅集中了500Hz信号的能量,还因为离505Hz太近,包含在其主瓣内,分到了505Hz频点信号的能量,因此幅度变得特别大。而1010Hz离得很远,只分到了一点点的能量,所以它的幅度也不是整数。(具体该是多少我们下一章节讨论)
由此可见,如果需要缓解频谱泄露的问题,如何选择一个好的窗函数是很重要的。
这篇关于关于涉及频谱分辨率的一些问题以及FFT幅度谱数值矫正问题的梳理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








