免费期货量化交易软件：种群优化算法引力搜索算法（GSA）

1. 概述

​​​​​​​

 

 

 

引力搜索算法（GSA）是由 E. Rashedi 提出的，用于解决优化问题，特别是非线性问题，它遵循牛顿的万有引力定律原理。 在所提议的算法中，粒子被视为物体，并在考虑其质量的情况下估算其性能。 引力是质量相互加速的趋势。 它是自然界中的四种基本力之一（其它是电磁力、弱核力和强核力）。

宇宙中的每个粒子都会吸引其它粒子。 重力无处不在。 虽然它是最弱的力量，但它是最可观的力量。 由于引力，人们可以在地球上行走，行星可以绕太阳运行。 任何物体的引力都与其质量成正比。 因此，质量更大的物体具有更大的引力。 重力的必然性令它与所有其它自然力区分开来。 牛顿引力的行为方式称为远距离作用。 它是从经验观察中推导出的一般物理定律，艾萨克·牛顿（Isaac Newton）称其为归纳推理。 它是牛顿的《自然哲学数学原理》中阐述的经典力学的一部分，该书于 1687 年 7 月 5 日首次出版。

1686 年 4 月，当牛顿向皇家学会提交第一本未出版的书稿时，罗伯特·胡克（Robert Hooke）声称牛顿是从他那里得到了平方反比定律。 用今天的语言来说，定律说所有“点质量”通过沿任两点连线的作用力吸引所有其它“点质量”。

2. 算法

本文提出了一种基于牛顿万有引力定律的优化算法：“宇宙中的每个粒子都按照与其质量乘积成正比，且与它们之间距离的平方成反比的作用力吸引所有其它粒子”。 在所提出的算法中，搜索代理者是一组基于牛顿引力和运动定律相互作用的质量。 与此同时，所有代理者都可以依据质量（根据目标函数的值计算）和它们之间的距离的吸引力相互交换信息，无论它们在搜索空间中的哪个位置。

代理者被视为物体，它们的适应性由其质量来衡量。 一般来说（算法设置接近真实的物理定律），所有这些物体都被引力相互吸引，这种力导致所有物体的全局运动向质量较大的物体靠拢。 因此，质量通过引力按直接形式的连接进行相互作用。

在经典的 GSA 中，每个粒子都有三种质量：

a) 主动质量
b) 被动质量
c) 惯性质量

在大多数情况下，利用这些概念的相等性来简化代码和计算，提高算法搜索能力的效率，是方便快捷的。 故此，算法中只有一个质量，而不是三个。 GSA 中所用的物理定律方程如图例 1 所示。

图例 1. 引力、加速度和速度

粒子的位置提供了问题的解决方案，而适应度函数用于计算质量。 该算法有两个阶段：探索和开拓。 该算法在开始时运用情报能力来避免陷入局部最优，之后则利用了极值区域。

引力搜索算法必须将空间中运动的粒子变成具有一定质量的物体。 这些物体由于彼此之间的引力相互作用而被吸引，空间中的每个粒子都会受粒子的相互吸引而产生加速度。 每个粒子都被其它粒子吸引，并沿力的方向移动。 质量较小的粒子向质量较大的粒子移动，但大质量物体自身也会移动，但速度较低，与质量成反比。 最优解是由“大”物体找到，比之移动速度更快的“小”物体，它们通过低速移动来完善系统的解。 GSA 通过对象之间的交互实现信息传输。

GSA 步骤:

1. 代理者初始化
2. 适应度进化
3. 引力常数计算
4. 代理者质量计算

1. 代理者初始化。
所有代理者都是随机初始化的。 每个代理者都被视为候选解。 为了令稳定性分析有意义和可靠，指定均衡的初始条件非常重要。 毕竟，如果物体的原始“碟状”不处于均衡状态，它在模拟步骤的第一次放松会导致不稳定，这对我们理解“碟状星系”的稳定性有一点重要。 不幸的是，在暗物质光环和/或星盘的外部势影响下的三维气态碟状的密度、速度场和温度，其流体静力均衡的计算，尚无已知的可分析解。
2. 适应度进化。
GSA 的可靠性和有效性取决于研究和探索能力之间的均衡。 在搜索最优解过程的初始迭代中，优先探索搜索空间。 这可以通过允许代理者在早期迭代中采用较大的步长来实现。 在稍后的迭代中，需要细化搜索空间，从而避免缺少全局最优解的情况。 因此，候选解应具有较小步长，以便在后续迭代中使用。

3. 引力常数计算
引力常数（也称为万有引力常数、牛顿万有引力常数、或卡文迪什引力常数），用字母 G 表示，是艾萨克·牛顿的万有引力定律和阿尔伯特·爱因斯坦的广义相对论中涉及引力效应计算的经验物理常数。 在牛顿定律中，它是将两个物体之间的引力与它们的质量乘积和距离的平方反比关联起来的比例常数。 在爱因斯坦场方程中，它量化了时空几何与能量-动量张量之间的关系。

4. 代理者质量计算。
质量是存在于空间中的物质含量。

算法伪代码：

1. 随机生成物体系统。
2. 判定每个物体的适应度。
3. 更新引力常数的值，计算质量，最佳和最差物体。
4. 计算每个坐标上的作用力。
5. 计算物体加速度和速度。
6. 更新物体的位置。
7. 判定每个物体的适应度。
8. 从第 3 步开始重复，直到满足终止条件。

赫兹期货量化来研究一下 GSA 代码。 为了描述引力相互作用系统中的物体，赫兹期货量化需要 S_Object 结构，它定义满足物体进行引力搜索的所有必要物理属性：c [] - 搜索空间中的坐标，v [] - 每个坐标的速度矢量（数组维度即坐标的数量）， M 是物体质量（在 GSA 中，质量是一个相对值，这是取决于整个物体系统中最大和最小适应度计算出的一个值），f 是适应度值，R [] 是到其它物体的欧几里德距离（数组的维度即物体的数量）， F [] 是每个坐标的作用力矢量（数组的维度即坐标数量）。

//——————————————————————————————————————————————————————————————————————————————
struct S_Object
{double c  [];   //coordinatesdouble v  [];   //velocitydouble M;       //massdouble f;       //fitnessdouble R  [];   //euclidean distance to other objectsdouble F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

赫兹期货量化来声明引力搜索算法的类 C_AO_GSA。 作为代理者，在算法里物体参与的物理属性之外，只需要一件事：表示最佳解的坐标 — fB 的值。 该类声明搜索空间坐标和步骤的有效范围。 受引力束缚的物体系统表示为 S_Object 结构的数组。 在经典算法中，只有三个外部参数：G_constant、a_constant、e_constant，它们决定了物体引力相互作用的属性，其余的常数都包含在计算方程中，但我考虑将这些相应常数移到算法的外部参数中，这样可以更灵活地调整整个算法的属性。 稍后我将更详细地研究所有参数，因为它们极大地影响了算法的行为。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GSA
{//----------------------------------------------------------------------------public: S_Object o       []; //objectpublic: double rangeMax  []; //maximum search rangepublic: double rangeMin  []; //manimum search rangepublic: double rangeStep []; //step searchpublic: double cB        []; //best coordinatespublic: double fB;           //FF of the best coordinatespublic: void Init (const int    coordinatesNumberP, //coordinates numberconst int    objectsNumberP,     //objects numberconst double PowerOfdistanceP,   //power of distanceconst double GraviPert_MinP,     //gravitational perturbation Minconst double GraviPert_MaxP,     //gravitational perturbation Minconst double VelocityPert_MinP,  //Velocity perturbation Minconst double VelocityPert_MaxP,  //Velocity perturbation Maxconst double G_constantP,        //G constantconst double a_constantP,        //a constantconst double e_constantP,        //e constantconst int    maxIterationsP);    //max Iterationspublic: void Moving   (int iter);public: void Revision ();//----------------------------------------------------------------------------private: int    coordinatesNumber; //coordinates numberprivate: int    objectsNumber;     //objects numberprivate: double PowerOfdistance;   //power of distanceprivate: double GraviPert_Min;     //gravitational perturbation Minprivate: double GraviPert_Max;     //gravitational perturbation Minprivate: double VelocPert_Min;     //velocity perturbation Minprivate: double VelocPert_Max;     //velocity perturbation Maxprivate: double G_constant;        //G constantprivate: double a_constant;        //a constantprivate: double e_constant;        //e constantprivate: int    maxIterations;private: bool   revision;private: double SeInDiSp  (double In, double InMin, double InMax, double Step);private: double RNDfromCI (double min, double max);private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Init() 算法的公开方法用于将算法的外部参数传递给内部常量，以便初始化服务变量，并为数组分配大小。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Init (const int    coordinatesNumberP, //coordinates numberconst int    objectsNumberP,     //objects numberconst double PowerOfdistanceP,   //power of distanceconst double GraviPert_MinP,     //gravitational perturbation Minconst double GraviPert_MaxP,     //gravitational perturbation Minconst double VelocityPert_MinP,  //Velocity perturbation Minconst double VelocityPert_MaxP,  //Velocity perturbation Maxconst double G_constantP,        //G constantconst double a_constantP,        //a constantconst double e_constantP,        //e constantconst int    maxIterationsP)     //max Iterations
{MathSrand ((int)GetMicrosecondCount ()); // reset of the generatorfB       = -DBL_MAX;revision = false;coordinatesNumber = coordinatesNumberP;objectsNumber     = objectsNumberP;PowerOfdistance   = PowerOfdistanceP;GraviPert_Min     = GraviPert_MinP;GraviPert_Max     = GraviPert_MaxP;VelocPert_Min     = VelocityPert_MinP;VelocPert_Max     = VelocityPert_MaxP;G_constant        = G_constantP;a_constant        = a_constantP;e_constant        = e_constantP;maxIterations     = maxIterationsP;ArrayResize (rangeMax,  coordinatesNumber);ArrayResize (rangeMin,  coordinatesNumber);ArrayResize (rangeStep, coordinatesNumber);ArrayResize (o,  objectsNumber);for (int i = 0; i < objectsNumber; i++){ArrayResize (o [i].c,  coordinatesNumber);ArrayResize (o [i].v,  coordinatesNumber);ArrayResize (o [i].R,  objectsNumber);ArrayResize (o [i].F,  coordinatesNumber);o [i].f  = -DBL_MAX;}ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

第一个公铠1方法在 Moving() 的每次迭代时调用。 该方法包含 GSA 算法的所有物理场和逻辑。 它有些庞大，所以我们考虑把它分成几部分。 请注意，该方法以当前迭代为参数，该参数涉及引力常数的计算，调整研究和探索i之间的平衡。

在第一次迭代中，会产生物体初始化阶段。 对于物体的所有坐标，赫兹期货量化在允许范围内分配随机值，均匀分布，并检查是否超出范围。 在优化过程伊始，所有物体的速度为零，也就是说，物体在搜索空间中相对坐标均是静止的。 请注意，物体没有质量，如此它们必须以光速移动，但我们将在第一次迭代中打破物理定律，因为这一刻在某种程度上相当于宇宙大爆炸。 此时物体的适应度是“双精度”数值的最小可能值。 调试算法时，很难找到与零质量相关的错误，您可以在下面看到解。

//----------------------------------------------------------------------------
if (!revision)
{fB = -DBL_MAX;for (int obj = 0; obj < objectsNumber; obj++){for (int c = 0; c < coordinatesNumber; c++){o [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);o [obj].v [c] = 0.0;o [obj].M     = 0.0;o [obj].f     = -DBL_MAX;}}revision = true;
}

Moving () 方法的其余代码是指第二次和后续迭代，其中物体将获得质量、速度和加速度。

首先，我们需要计算质量。 如上所述，物体的质量（根据定义为正标量值）是根据适应度函数的值计算得出的，因此有必要在根据获得的值计算质量之前确定最小和最大适应度值。 至此，适应度函数的值已经在上一次迭代中得到了。

//find the minimum and maximum fitness==========================================
for (int obj = 0; obj < objectsNumber; obj++)
{if (o [obj].f < Fmin) Fmin = o [obj].f;if (o [obj].f > Fmax) Fmax = o [obj].f;
}

在代码的这一点上，计算质量是使用方程 Mo=(Fo-Fmin)/(Fmax-Fmin)，其中：

• Mo - 物体质量
• Fo - 物体适应度
• Fmax - 所有物体中的最大适应度值（最佳值）
• Fmin - 所有物体中的最小适应度值（最差值）

正如我们从方程中所见，质量只能取 0 到 1 范围内的正值（包括 0 和 1）。 由于我们之前讨论过质量不能等于零，否则速度将等于光速，我们将质量的下限限制为 1.1。 上限值很可能等于 1。 另外，请记住，如果适应度函数的最小值和最大值相等，则所有物体的质量对于都相同，且等于 1。 这对应于以下情况：搜索空间在物体所在的区域中是均匀的，并且所有物体在适应度函数的质量方面都是相等的，并且任何方向的运动都具有相同的优先级。 在这种情况下，似乎所有物体都应该逐渐移动，并集中到一个共同的质心，但由于引力的非线性作用，这实际上并不会发生。

//calculating the mass of objects===========================================
for (int obj = 0; obj < objectsNumber; obj++)
{Fo = o [obj].f;if (Fmax == Fmin) Mo = 1.0;else Mo = (Fo - Fmin) / (Fmax - Fmin);o [obj].M = Scale (Mo, 0.0, 1.0, 0.1, 1.0, false);
}

我们已经计算了物体的质量，现在有必要计算 R 方程的另一个分量 — 从每个物体到其它独立物体的欧几里德距离。 计算包括两个物体枚举周期和每个坐标的计算周期。 我们仍记得，欧几里德距离是坐标差值平方和的根。

//calculation of Euclidean distances between all objects====================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].R, 0.0);for (int obj = 0; obj < objectsNumber; obj++)
{for (int obj2 = 0; obj2 < objectsNumber; obj2++){if (obj != obj2){if (o [obj].R [obj2] == 0.0){for (int c = 0; c < coordinatesNumber; c++){diffDist = o [obj].c [c] - o [obj2].c [c];o [obj].R [obj2] += diffDist * diffDist;}o [obj].R [obj2] = sqrt (o [obj].R [obj2]);o [obj2].R [obj] = o [obj].R [obj2];}}}
}

现在赫兹期货量化可以计算物体的作用力矢量。 为此，我们还需要在两个循环遍历所有对象，并在一个周期中获取坐标，因为每个坐标的速度是单独计算的。 我们必须添加一个排除物体索引重合的条件，以便物体在力计算中排除自身的计算。 在此，我们使用牛顿著名的方程来计算两个物体的引力（图例 1），通过 e_constant 比率校正距离。 我们首先计算引力常数 G，其在每次迭代时应该向下变化，假设在优化结束时算法强度加剧。

//calculate the force vector for each object================================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].F, 0.0);double G = G_constant * exp (-a_constant * (iter / maxIterations));for (int obj = 0; obj < objectsNumber; obj++)
{for (int obj2 = 0; obj2 < objectsNumber; obj2++){if (obj != obj2){for (int c = 0; c < coordinatesNumber; c++){diffDist = o [obj2].c [c] - o [obj].c [c];if (o [obj].R [obj2] != 0.0){o [obj] .F [c] += G * o [obj].M * o [obj2].M * diffDist / (pow (o [obj].R [obj2], PowerOfdistance) + e_constant);}}}}
}

现在我们只需要计算速度，物体就可以开始移动。 从图例 1 中的方程中，我们可以看到速度计算涉及加速度，而加速度等于作用在物体上的力除以质量。 该方程还包含时间 V=V0+a*t。 在我们的算法中，迭代扮演着时间的角色，所以速度的变化无非是一次迭代中速度的增加。 速度矢量已经在上面计算过了。 它仍然要按质量划分。 此外，作者还引入了作用力扰动和速度扰动。 扰动是介于 0 和 1 之间的均匀分布的随机数。 这为物体的运动增加了一个随机分量，没有它的话运动就被严格确定，并且仅取决于物体的初始位置。 我认为将扰动指标引入算法的外部参数是合理的，这允许把物体的运动从完全确定性调节到完全随机。

//calculation of acceleration and velocity for all objects==================
double a = 0.0; //accelerationfor (int obj = 0; obj < objectsNumber; obj++)
{for (int c = 0; c < coordinatesNumber; c++){r = RNDfromCI (GraviPert_Min, GraviPert_Max);a = o [obj].F [c] * r / o [obj].M;r = RNDfromCI (GraviPert_Min, GraviPert_Max);o [obj].v [c] = o [obj].v [c] * r + a;o [obj].c [c] = o [obj].c [c] + o [obj].v [c];if (o [obj].c [c] > rangeMax [c]) o [obj].c [c] = rangeMin [c];if (o [obj].c [c] < rangeMin [c]) o [obj].c [c] = rangeMax [c];o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);}
}

第二个 Revision () 方法，在每次迭代时都必须执行。 该方法旨在判定当前迭代的最佳适应度值。 在循环中，遍历所有物体，并替换全局最佳解。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Revision ()
{for (int s = 0; s < objectsNumber; s++){if (o [s].f > fB){fB = o [s].f;ArrayCopy (cB, o [s].c, 0, 0, WHOLE_ARRAY);}}
}
//——————————————————————————————————————————————————————————————————————————————

3. 测试结果

赫兹期货量化转至测试结果。 以下是我能找到的最优 GSA 参数的测试台结果：

2023.02.03 14:12:43.440 Test_AO_GSA (EURUSD,M1) C_AO_GSA:10;2.0;0.2;0.6;0.0;1.0;2.0;20.0;0.01
2023.02.03 14:12:43.440 Test_AO_GSA (EURUSD,M1) =============================
2023.02.03 14:12:52.198 Test_AO_GSA (EURUSD,M1) 5 Rastrigin's; Func runs 10000 result: 73.64619475145881
2023.02.03 14:12:52.198 Test_AO_GSA (EURUSD,M1) Score: 0.91252
2023.02.03 14:13:06.105 Test_AO_GSA (EURUSD,M1) 25 Rastrigin's; Func runs 10000 result: 59.4327218024363
2023.02.03 14:13:06.105 Test_AO_GSA (EURUSD,M1) Score: 0.73640
2023.02.03 14:14:16.529 Test_AO_GSA (EURUSD,M1) 500 Rastrigin's; Func runs 10000 result: 37.550565227034724
2023.02.03 14:14:16.529 Test_AO_GSA (EURUSD,M1) Score: 0.46527
2023.02.03 14:14:16.529 Test_AO_GSA (EURUSD,M1) =============================
2023.02.03 14:14:30.577 Test_AO_GSA (EURUSD,M1) 5 Forest's; Func runs 10000 result: 0.741456333008312
2023.02.03 14:14:30.577 Test_AO_GSA (EURUSD,M1) Score: 0.41941
2023.02.03 14:14:50.281 Test_AO_GSA (EURUSD,M1) 25 Forest's; Func runs 10000 result: 0.46894018717768426
2023.02.03 14:14:50.282 Test_AO_GSA (EURUSD,M1) Score: 0.26526
2023.02.03 14:16:01.856 Test_AO_GSA (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.11382493516764165
2023.02.03 14:16:01.856 Test_AO_GSA (EURUSD,M1) Score: 0.06439
2023.02.03 14:16:01.856 Test_AO_GSA (EURUSD,M1) =============================
2023.02.03 14:16:18.195 Test_AO_GSA (EURUSD,M1) 5 Megacity's; Func runs 10000 result: 5.279999999999999
2023.02.03 14:16:18.195 Test_AO_GSA (EURUSD,M1) Score: 0.44000
2023.02.03 14:16:34.536 Test_AO_GSA (EURUSD,M1) 25 Megacity's; Func runs 10000 result: 2.296
2023.02.03 14:16:34.536 Test_AO_GSA (EURUSD,M1) Score: 0.19133
2023.02.03 14:17:46.887 Test_AO_GSA (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.23399999999999999
2023.02.03 14:17:46.887 Test_AO_GSA (EURUSD,M1) Score: 0.01950

算法参数:

input double PowerOfdistance_P = 2.0; //Power of distance
input double GraviPert_Min_P = 0.2; //Gravitational perturbation Min
input double GraviPert_Max_P = 0.6; //Gravitational perturbation Max
input double VelocityPert_Min_P = 0.0; //Velocity perturbation Min
input double VelocityPert_Max_P = 1.0; //Velocity perturbation Max
input double G_constant_P = 2.0; //G constant
input double a_constant_P = 20.0; //a constant
input double e_constant_P = 0.01; //e constant

PowerOfdistance_P - 我们提升物体之间距离的角度，其会影响引力束缚物体的形成。 方程中的角度越高，物体对其它物体的影响越小。

• GraviPert_Min_P - 引力摄动范围的下限。
• GraviPert_Max_P - 引力摄动范围的上限。
• 若 GraviPert_Min_P = 1.0 且 GraviPert_Max_P = 1.0，没有引力扰动。
• VelocityPert_Min_P - 速度扰动范围的下限。
• VelocityPert_Max_P - 速度扰动范围的上限。

若 VelocityPert_Min_P = 1.0 且 VelocityPert_Max_P = 1.0，没有速度扰动。

• G_constant_P - 引力常数充当比例因子：值越高，引力作用越强，物体的速度变化越快。
• a_constant_P - 引力常数的校正因子，旨在在整个优化过程中减小搜索区域，以便细化发现的极值。
• e_constant_P - 物体间距离的校正因子。

我们看一下可视化测试结果。 算法在测试函数上的行为非常奇特和有趣。 事实上，实验展示了引力的作用。 物体的移动和所得优化结果受到算法外部参数的强烈影响。 最初，速度为零的物体随机分布在搜索空间之中，并在下一次迭代时开始移动。 测试中所用的设置（我发现的最好的设置）令物体向共同的质心移动。

不要忘记每个物体的引力都会影响其它物体，这些物体的运动定律在算法中以足够高的精度描述。 接近共同的质心，物体继续高速移动。 它看起来像是大量粒子向共同质心并来回拉扯的脉动运动。 经过一定次数的迭代后，物体的运动在适应度函数的空间起伏的影响下改变其轨迹，可视为影响物体质量的引力不均匀性。 正如我们前面所讨论的，物体的质量是根据适应度函数的值计算得出的。 然而，沿轴对称的 Rastrigin 函数对物体的运动具有相当均匀的影响，并且分解成组，故并不是特别明显。

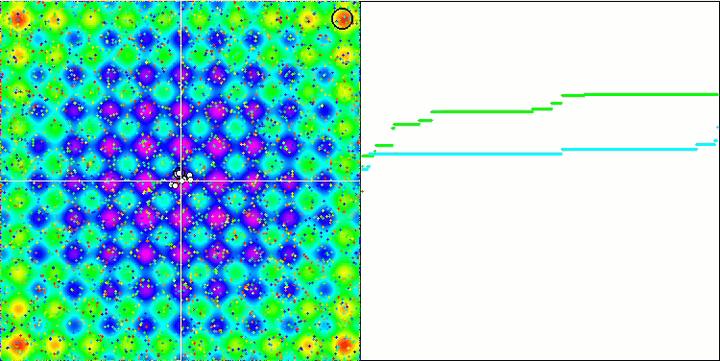
基于 Rastrigin 测试函数的 GSA 。

Forest 和 Megacity 函数中的物体显示了更有趣的行为。 这些函数不是对称的，因此对整个物体组具有不均匀的影响。

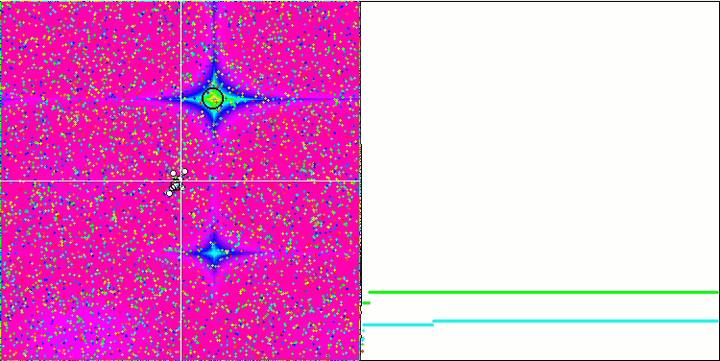
GSA on the Forest test function.

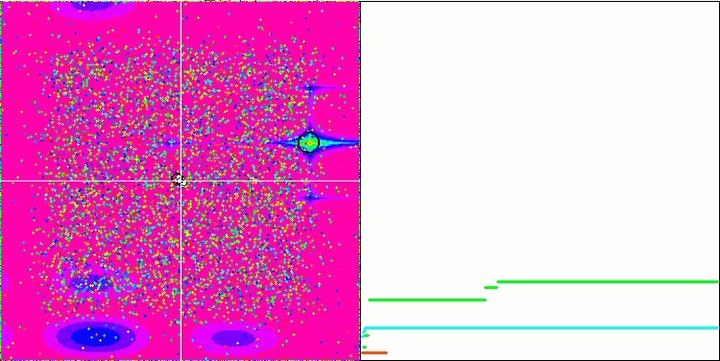
Megacity 测试函数上的 GSA。

在针对 GSA 进行了大量实验之后，我迸发出制作空间物体运动模拟器的想法。 它并没有实用价值，但它能给出作用于行星和恒星系统的物理定律的概念。 模拟器是禁用随机性的 GSA 版本。 此外，还介绍了三个模仿三颗恒星（蓝巨星，黄星和白矮星）的物体。 质量参数在它们的设置中单独显示。

创建了一个新的 Universe 适应度函数，专门为模拟器创建了一个统一的空间。 模拟器清楚地显示了物体之间距离的度数（参数）如何影响它们的相互运动。 在下面的可视化中，应用 3 的幂，来替代牛顿定律的标准值 2。 很明显，度数如何影响引力束缚系统的形成，例如双星和三星系统。

如果在赫兹期货量化的宇宙中距离更高，那么星系的形成就会比现实中早得多。 动画清楚地表明，围绕共同质心循环的成对物体在第一次迭代中就出现了。 正如预期，这颗蓝巨星吸引周围的物体最多。

基于 GSA 算法的空间物体运动模拟器可视化

赫兹期货量化继续分析 GSA 测试结果。 算法中所用的原始特征不允许它在我们的测试中获得强大的结果。 我尝试参数的多种变化，却并没有提高算法的收敛性。 该算法在具有 10 个变量和 Megacity 的平滑 Rastrigin 函数上显示出相对于其它测试参与者的一些积极结果。 而在其它测试中，GSA 的表现低于表格中的平均水平，在 8 个测试中排名第 12。

算法	说明	Rastrigin	Rastrigin 最终	Forest	Forest 最终	Megacity (离散)	Megacity 最终	最终结果
10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)	10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)	10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)
IWO	入侵杂草优化	1.00000	1.00000	0.35295	2.35295	0.79937	0.46349	0.41071	1.67357	0.75912	0.44903	0.94416	2.15231	100.000
ACOm	蚁群优化 M	0.36118	0.26810	0.20182	0.83110	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.15901	2.15901	96.805
COAm	杜鹃优化算法 M	0.96423	0.69756	0.30792	1.96971	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.48451	1.49877	74.417
FAm	萤火虫算法 M	0.62430	0.50653	0.20290	1.33373	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	70.740
BA	蝙蝠算法	0.42290	0.95047	1.00000	2.37337	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.49268	0.71755	59.383
ABC	人工蜂群	0.81573	0.48767	0.24656	1.54996	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.39496	1.13621	57.393
BFO	细菌觅食优化	0.70129	0.46155	0.13988	1.30272	0.41251	0.26623	0.26695	0.94569	0.42336	0.34491	0.53694	1.30521	55.563
GSA	引力搜索算法	0.73222	0.67404	0.00000	1.40626	0.31238	0.36416	0.42921	1.10575	0.51095	0.36658	0.00000	0.87753	52.786
FSS	鱼群搜索	0.48850	0.37769	0.13383	1.00002	0.78060	0.05013	0.08423	0.91496	0.00000	0.01084	0.23493	0.24577	20.094
PSO	粒子群优化	0.21339	0.12224	0.08478	0.42041	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.05550	0.15963	14.358
RND	随机	0.17559	0.14524	0.09495	0.41578	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.13960	0.13960	8.117
GWO	灰狼优化器	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.07252	0.30348	1.000

通常，GSA 算法对于正在优化的函数中是否存在梯度非常敏感。 低可扩展性不允许将其用于包含许多变量的严肃任务，因此我不建议将该算法用于神经网络和优化交易系统。 我还没有彻底研究引力搜索算法的可能性。 深入的研究可能会为这种非常有趣和不寻常的算法打开新的未知积极特征。 该算法的主要优点是独立于当前找到的全局最优解，以及所有代理者相互交互的能力。

图例. 2 展示算法的测试结果

图例 2. 算法测试结果的直方图

关于引力搜索算法（GSA）性质的结论：

优点:
1. 易于实现。
2. 在变量较少的平滑函数上表现良好。

缺点:
1. 计算复杂度高。
2. 离散函数结果低下。
3. 可扩展性差。