本文主要是介绍数据结构基础:P4-树(中)----编程作业01:是否同一棵二叉搜索树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本系列文章为浙江大学陈越、何钦铭数据结构学习笔记,系列文章链接如下:
数据结构(陈越、何钦铭)学习笔记
文章目录
- 题目描述
- 一、题意理解及搜索树表示
- 1.1 题意理解
- 1.2 解题思路
- 二、程序框架及建树
- 三、探索树是否一样的判别
- 四、整体代码
题目描述
题目描述: 给定一个插入序列就可以唯一确定一棵二叉搜索树。然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。任务是对于输入的各种插入序列,判断它们是否能生成一样的二叉搜索树。
输入格式: 输入包含若干组测试数据。每组数据的第1行给出两个正整数 N (≤10) 和 L,分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数,作为初始插入序列。最后L行,每行给出N个插入的元素,属于L个需要检查的序列。简单起见,我们保证每个插入序列都是1到N的一个排列。当读到N为0时,标志输入结束,这组数据不要处理。
输出格式: 对每一组需要检查的序列,如果其生成的二叉搜索树跟对应的初始序列生成的一样,输出"Yes",否则输出"No"。
输入样例:
4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0
输出样例:
Yes
No
No
一、题意理解及搜索树表示
1.1 题意理解
给定一个插入序列就可以唯一确定一棵二叉搜索树。然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到。
例如:按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。
问题:对于输入的各种插入序列,你需要判断它们是否能生成一样的二叉搜索树
输入样例:
4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0
输出样例:
Yes
No
No
输入样例的解释:
输入样例中,每组数据包含三部分的内容。
①第一部分内容是两个整数,第一个整数是这个插入的序列的个数,也就是说二叉搜索树的结点个数,我们这里是4。第二个整数在我们这里是2,他代表后面有2个序列需要跟前面去比较是不是一样的。
②第二部分的内容代表了输入的序列。
③第三组数据就是后面的若干组输入的序列,他们全部要跟第一组输入序列做比较,看看是不是一样。
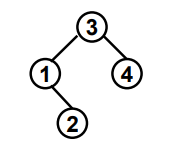
对于上面输入的原始序列为3 1 4 2,其二叉平衡树结构为:
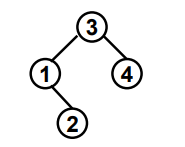
后面的序列3 4 1 2的二叉平衡树结构如下所示。可以看出结构一样,所以输出Yes。
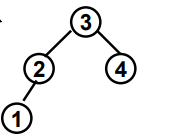
后面的序列3 2 4 1,其平衡二叉树结构如下所示。可以看出结构不一样,所以输出No。
1.2 解题思路
给你两个序列,你怎么判断他对应的搜索树是不是一样,这是我们最基本的一个问题。这样的一种判断共有三种方法。
①分别建两棵搜索树的判别方法
首先一种,根据这两个序列,我分别构造两棵搜索树,然后比较这两棵搜索树是否一样。比较两棵搜索树是否一样,方法很简单。首先看根结点是否一样,然后看左子树是否一样,右子树是否一样,这样递归就可以实现了。
②不建树的判别方法
我们想比较3 1 2 4和3 4 1 2这两个序列所对应的二叉搜索树是否一样。其实很简单,我们首先比较第一个整数是否一样。第一个整数都是3,就说明了它们所对应的根结点是一样的。然后根据这个根结点3,我们可以把序列后面的几个数分成两堆。一个比3小的一堆,一个比3大的一堆,当然顺序还是按原来的顺序。所以这样就可以把3 1 2 4以3为基准,分为比他小的1 2 和比他大的4。那这1 2就意味了是作为3的左子树,4是作为3的右子树。同样的,3 4 1 2 我们以3为基准,按照原来的顺序就分为比他小的1 2和比他大的4。那么这样的话比较两个序列所对应的二叉搜索树是否一样就变成比较两个左子树是否一样,两个右子树是否一样。我们一看就知道这两个序列是完全一样的,所以这两组序列所对应的搜索树是一样的。
我们来看另外一组数据,3 1 2 4跟3 2 4 1。对于3 2 4 1,以3为基准,比他小的数的序列是2 1,比他大的序列是4,所以结果如下,可以看出不相等。
③建一棵树,再判别其他序列是否与该树一致
我们建一棵树,把这个树作为基准,然后把要比较的序列跟这个树去比较,看看这个序列跟这个树是不是一致的。根据这样的一种思路,我们的关键问题有这么几个:
----搜索树如何表示
----如何建立搜索树T
----如何判别一序列是否与搜索树T一致
关于搜索树怎么表示这个问题,我们可以采用最经典的搜索树的表示方法。
typedef struct TreeNode *Tree;
struct TreeNode {int v;Tree Left, Right;int flag;
};
代码对应解释:
我们用链表的形式来表示搜索树,每个结点是一个结构。这个结构里面有两个指针,一个left和一个right,指向左右孩子。用 v 来表示这个节点的基本信息。这里我们多了一个阈flag,这个 flag 就是我们后面用来判别一个序列是不是跟树一致需要用到的信息。flag 的实际含义就是:如果某个结点没被访问过,flag 设为0。被访问过了, flag就设为1。所以这个 flag 是作为有没被访问过的一个标记,将来这个标记很重要。
二、程序框架及建树
我们对每组数据要处理三件事情:
①第一件事情要把N跟L读进来。N就代表我们的这个序列的元素的个数,也是说搜索树的结点个数。L代表有多少个序列需要比较。
②把N跟L两个整数都进来了之后,接下来要根据第一行的序列来构建我们的基准树T。
③我们要分别读入后面L个序列来跟T做比较,看看是不是一致的。如果是一致,那我们就输出 yes,不一样的就输出 no。
对应框架如下:
int main()
{
对每组数据:读入N和L根据第一行序列建树T依据树T分别判别后面的L个序列是否能与T形成同一搜索树并输出结果return 0;
}
对应代码如下:
int main()
{ int N, L, i;Tree T;scanf("%d", &N); //输入结点数while (N) {scanf("%d", &L); //输入后面有L个序列要比较T = MakeTree(N);//创建一棵二叉搜索树for (i=0; i<L; i++) { //逐次比较L个序列if (Judge(T, N))printf("Yes\n");else printf("No\n");ResetT(T); /*清除T中的标记flag*/ //比较一个序列后需要将原始树上的标记清除}FreeTree(T);//释放这棵树scanf("%d", &N); //重新读入N,可能会继续创建树并比较}return 0;
}
其中,建树、插入等操作代码如下:
//建立一棵树
Tree MakeTree( int N )
{ Tree T;int i, V;scanf("%d", &V); //先输入头结点T = NewNode(V); //创建一棵树的头结点for (i=1; i<N; i++) { //依次插入剩下的N-1个结点scanf("%d", &V);T = Insert(T, V);}return T;
}//插入一个结点
Tree Insert( Tree T, int V )
{//如果T为空,则创建头结点if ( !T ) T = NewNode(V);else { if ( V>T->v ) //要插入的值大于结点值,插在右子树T->Right = Insert( T->Right, V );else //要插入的值小于结点值,插在左子树T->Left = Insert( T->Left, V );}return T;
}//创建一颗新树
Tree NewNode( int V )
{ Tree T = (Tree)malloc(sizeof(struct TreeNode));T->v = V;T->Left = T->Right = NULL;T->flag = 0;return T;
}
三、探索树是否一样的判别
接下来到我们最关键的一步,要开始判别后面输入的序列所对应的二叉搜索树是否与原始的搜索树T相同。我们可以用种方法很容易做到:
把序列每个整数到这个树T里面去查找一下,如果在这个查找过程当中发现查找某个整数所经过的路径有某个结点是以前没碰到过的,那么这个序列跟这个树一定不一致。因为如果没碰到过,那么当前的这个整数就不应该插在后面,应该在没有碰到过的结点上就应该插入了,而不会再往下插的。所以我们把一个序列跟一个树是不是一致的这个判别转换成为查找这个序列中的每一个整数在这个树中的位置。
举个例子:
现在我有通过3 1 4 2构造的原始搜索树T,还有一个序列3 2 4 1。
对这个例子来讲,我们查找的序列是3 2 4 1。我们先找3,3是根节点,这是第一个数。所以马上就标记 flag 为1,就是我找过了。接下来找第二个数2,那么为了找2,他要从3开始查找,接下来要找到1,接下来再找到2。从3 1 2这个过程当中,3前面碰到过了,而1没碰到过,那么这个时候我们就可以断定这个序列3 2 4 1跟我们的T是不一致的。
判别对应的代码如下:
int check ( Tree T, int V )
{//如果当前结点被访问了if ( T->flag ) {//根据V的值去当前结点的左右子树继续找if ( V<T->v ) return check(T->Left, V);else if ( V>T->v ) return check(T->Right, V);//如果相等就意味的在这个序列里面有两个整数是出现了两次以上,就重复出现了,那么这个时候我们认为是不一致的else return 0;}//如果当前结点没被访问,就要看当前结点的v是不是我要找的值else {//如果值相等,说明原来没被找过,现在正好是我要找的这个结点//就将flag置为1,并return 1if ( V==T->v ) {T->flag = 1;return 1;}//否则说明碰到了一个以前没见到过的结点,就return 0else return 0;}
}
有了check这个函数之后,我们整个Judge的判别就变成是判别这N元素的序列每一个整数是不是一致的。所以我们去执行一系列的check操作,对应的整体Judge代码(有BUG)如下:
int Judge( Tree T, int N ) /* 有bug版本 */
{int i, V; scanf("%d", &V);//先判断输入的V是否和树的根结点的值相等。如果不等,则两棵树一定不一样if ( V!=T->v ) return 0;//如果相等则说明树根相等,将flag置1,并继续对后面N-1个数进行检查else T->flag = 1;for (i=1; i<N; i++) {scanf("%d", &V);//如果check不成功,就返回0if (!check(T, V) ) return 0;}return 1;
}
上面代码有一些问题:
问题在于:我们要连续L个序列跟T去做比较,如果在处理某个序列的时候,某个数发现是不一致的,那么这个时候按照我们现在这个程序,这个Judge要ruturn出来。比方说我们上面的例子,3是一致的,即树根是一致的。去找2,要经过1,说明是不一致了。在程序中读完2了之后发现不一致就return 0 出来了,一return出来了之后意味着要进入下一轮序列的检查。就会把这个序列的后面几个数就4跟1当成是下个序列,那这个程序就是有问题了。所以当我们发现某个数不一致的时候,不能马上退出,必须把这一行的其他的整数全部读完然后才能够退出来。这样保证下一个序列是我们真正要求的这个序列。正确代码如下:
int Judge( Tree T, int N )
{int i, V, flag = 0; /* 这个flag是整个程序中的flag,不是结点中的那个flag: flag 等于0代表到目前为止,处理序列的过程中还认为是一致的,没有发生矛盾的情况。当 flag为1的时候就说明我们已经发现矛盾了,但是这个时候我们不能退出来,程序还要继续运行要把后面的几个整数都把它读完 */scanf("%d", &V);if ( V!=T->v ) flag = 1;else T->flag = 1;for (i=1; i<N; i++) {scanf("%d", &V);//如果有矛盾,直接不用check,直接读取下一个数if ( (!flag) && (!check(T, V)) ) flag = 1;}if (flag) return 0;else return 1;
}
此外,当前序列读完了之后我们要处理下个序列。在处理下个序列之前我们要把树上每个节点的 flag 标记全部清为0,所以叫Reset,他的目的就是把这个树上的每个节点的 flag 都清为0。我们一组数据处理完了之后,要进入下一组数据之前,要把当前这个树它释放掉。那么怎么释放空间,一样的道理也是递归,把左子树的空间释放,把右子树的空间释放,然后把当前根节点的空间释放。
void ResetT ( Tree T ) /* 清除T中各结点的flag标记 */
{if (T->Left) ResetT(T->Left);if (T->Right) ResetT(T->Right);T->flag = 0;
}void FreeTree ( Tree T ) /* 释放T的空间 */
{if (T->Left) FreeTree(T->Left);if (T->Right) FreeTree(T->Right);free(T);
}
四、整体代码
整体代码如下:
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>typedef struct TreeNode *Tree;
struct TreeNode {int v;Tree Left, Right;int flag;
};Tree MakeTree(int N); //建立一棵树
Tree Insert(Tree T, int V);//插入一个结点
Tree NewNode(int V); //创建一颗新树
int check(Tree T, int V); //
int Judge(Tree T, int N); //
void ResetT(Tree T); //清除T中各结点的flag标记
void FreeTree(Tree T); //释放T的空间int main()
{int N, L, i;Tree T;scanf("%d", &N); //输入结点数while (N) {scanf("%d", &L); //输入后面有L个序列要比较T = MakeTree(N);//创建一棵二叉搜索树for (i = 0; i < L; i++) { //逐次比较L个序列if (Judge(T, N))printf("Yes\n");else printf("No\n");ResetT(T); /*清除T中的标记flag*/ //比较一个序列后需要将原始树上的标记清除}FreeTree(T);//释放这棵树scanf("%d", &N); //重新读入N,可能会继续创建树并比较}return 0;
}//建立一棵树
Tree MakeTree(int N)
{Tree T;int i, V;scanf("%d", &V); //先输入头结点T = NewNode(V); //创建一棵树的头结点for (i = 1; i < N; i++) { //依次插入剩下的N-1个结点scanf("%d", &V);T = Insert(T, V);}return T;
}//插入一个结点
Tree Insert(Tree T, int V)
{//如果T为空,则创建头结点if (!T) T = NewNode(V);else {if (V > T->v) //要插入的值大于结点值,插在右子树T->Right = Insert(T->Right, V);else //要插入的值小于结点值,插在左子树T->Left = Insert(T->Left, V);}return T;
}//创建一颗新树
Tree NewNode(int V)
{Tree T = (Tree)malloc(sizeof(struct TreeNode));T->v = V;T->Left = T->Right = NULL;T->flag = 0;return T;
}int check(Tree T, int V)
{//如果当前结点被访问了if (T->flag) {//根据V的值去当前结点的左右子树继续找if (V < T->v) return check(T->Left, V);else if (V > T->v) return check(T->Right, V);//如果相等就意味的在这个序列里面有两个整数是出现了两次以上,就重复出现了,那么这个时候我们认为是不一致的else return 0;}//如果当前结点没被访问,就要看当前结点的v是不是我要找的值else {//如果值相等,说明原来没被找过,现在正好是我要找的这个结点//就将flag置为1,并return 1if (V == T->v) {T->flag = 1;return 1;}//否则说明碰到了一个以前没见到过的结点,就return 0else return 0;}
}int Judge(Tree T, int N)
{int i, V, flag = 0;/* 这个flag是整个程序中的flag,不是结点中的那个flag:flag 等于0代表到目前为止,处理序列的过程中还认为是一致的,没有发生矛盾的情况。当 flag为1的时候就说明我们已经发现矛盾了,但是这个时候我们不能退出来,程序还要继续运行要把后面的几个整数都把它读完 */scanf("%d", &V);if (V != T->v) flag = 1;else T->flag = 1;for (i = 1; i < N; i++) {scanf("%d", &V);//如果有矛盾,直接不用check,直接读取下一个数if ((!flag) && (!check(T, V))) flag = 1;}if (flag) return 0;else return 1;
}void ResetT(Tree T) /* 清除T中各结点的flag标记 */
{if (T->Left) ResetT(T->Left);if (T->Right) ResetT(T->Right);T->flag = 0;
}void FreeTree(Tree T) /* 释放T的空间 */
{if (T->Left) FreeTree(T->Left);if (T->Right) FreeTree(T->Right);free(T);
}
运行,输入测试样例,结果正确:
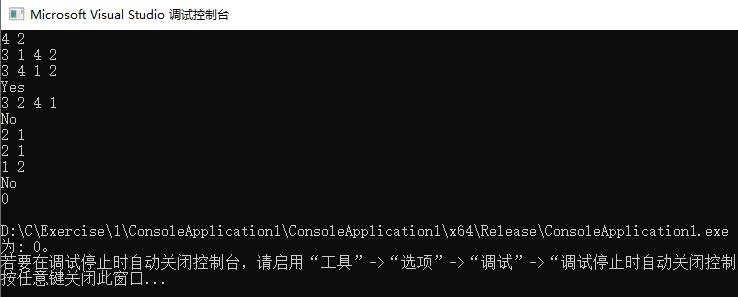
这篇关于数据结构基础:P4-树(中)----编程作业01:是否同一棵二叉搜索树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!