拉钩教育的数据分析课程归纳小结：数据分析中的概率统计初步

统计学基础当中描述性统计的基本概念：

 

首先，什么叫作推理性统计呢？

简而言之，推理性统计是通过样本数据去推理总体数据特性的方法。它跟描述统计不一样，描述统计是用整体的数据来描述整体特征，而推理统计是用部分数据来推理整体特征。我们经常说的假设检验、采样与过采样、回归预测模型、贝叶斯模型都是推理性统计。

下面我们分别介绍一下推理性统计当中的概率分布与假设检验的内容，这两个概念在数据分析中有着非常广泛的应用，概率分布常被用来进行数据规律预测，比如营销业务预测、进销存预测等；而假设检验则是解决数据问题的强大工具，产品管理、AB 测试等都利用了假设检验的思想。

天有不测风云的本质：概率分布

什么是概率分布呢？我们首先要了解一个重要概念——随机概率事件。

比如你去吃饭的时候可能要排多少人的队？今年冬天会不会下雪？明天的股票会不会涨？扔骰子是 6 的可能性有多大，等等。这些事件的发生是随机且存在一定可能性的，这种事件就称为“随机概率事件”。

我们常说的“天有不测风云”就是一种最直观的随机概率事件。

而我们会用随机变量来描述随机概率事件，这里涉及了两种常见的概率分布类型：离散型、连续型。

 

离散型分布

如果你随机发生的事件之间是毫无联系的，每一次随机事件发生都是独立的、不连续的、不受其他事件影响的，那么这些事件的概率分布就属于离散型分布。

比如计算我今天开车碰上交通事故的概率，交通事故的发生是独立的，不会因为昨天发生了交通事故，就会影响再次发生的可能性。

比较常见的离散型分布主要有三种：二项分布、几何分布和泊松分布。

二项分布

我们先不着急了解二项分布的定义，我们先来看看二项分布能解决什么问题，你自然就会明白它的定义了。

比如你向 3 家公司投递简历，会被其中一家录用的概率分布就是二项分布，也就是说二项分布解决的是发生次数固定、求成功次数概率的事件，但是要保证这些事件的结果只有两种结果，也就是非 A 即 B。

更形象的例子就是抛硬币，抛出 10 次硬币，求不同正面朝上的次数概率就符合二项分布，而想要求出具体的数值，就要用到二项分布的公式：

其中，p 表示概率，C 表示排列组合，n 表示试验次数，x 表示成功次数。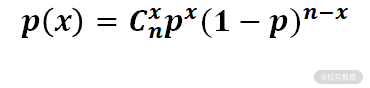

这个公式看似复杂，但其实你不必害怕，因为大多数数据分析工具都可以直接计算结果，比如 Excel 当中的 BINOMDIST 函数。因此你只需要掌握二项分布的概念和使用条件即可。

其中，1 或者 0 分别代表累积分布与概率分布，即 1 代表着最多成功 N 次的概率，而 0 代表着成功 N 次的概率，一般选择为 0 。

直白地看可能你会不明白，下面我结合具体的例子带你了解 BINOMDIST 函数的用法。

已知某公司产品不合格率为 10%，随机抽 50 个，求其中有 3 个产品不合格的概率。

使用 BINOMDIST 函数，分别输入不合格率、试验次数以及成功次数，即可快速计算出 50 个产品中有 3 个不合格的概率为 13.86%。是不是很好理解了？你可以自己动手尝试一下。

几何分布

几何分布与二项分布非常相似，唯一的区别就是几何分布是求试验几次才能获得第一次成功的概率，比如扔硬币扔到第几次才能第一次抛出正面的概率分布，即为几何分布。

因为二项分布是固定了试验次数，而几何分布是固定了成功次数，因此几何分布就是相当于二项分布成功累计 N 次的结果。

比如我在网上投递简历，失败一次就去另一家投递，求第几次投递时我才能第一次通过简历的概率，就符合几何分布，其计算公式为：

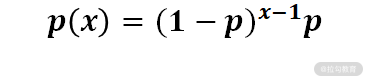
 泊松分布
 

与几何分布和二项分布不同的是，泊松分布是在一定的时间内，某个事件发生 N 次的概率分布，比如我一个月内闯红灯 30 次的概率、半年内旅游 10 次的概率。

为了方便你理解，我依然举个例子说明。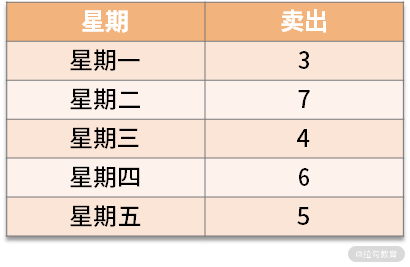

比如说，公司楼下有家馒头店：老板统计了一周每日卖出的馒头，均值为 5，但是如果每天都准备 5 个馒头，就会造成

为了方便你理解，我依然举个例子说明。

比如说，公司楼下有家馒头店：老板统计了一周每日卖出的馒头，均值为 5，但是如果每天都准备 5 个馒头，就会造成缺货。

那么需要准备多少个馒头才能保证自己不缺货呢？一天的时间可以分为 24 个小时，每小时都可能发生两件事：有顾客买、没有顾客买。

如果我们要预测一天当中卖多少个馒头的概率分别是多少，就可以用泊松分布来表示，我们可以直接用很多软件里自带的泊松回归来计算，比如 Excel 当中的 posson.dist 函数。

缺货。

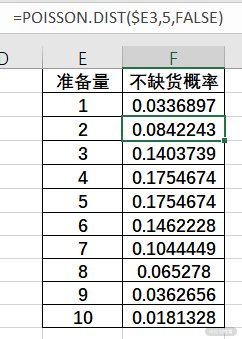
计算出准备 1~10 个馒头不缺货的概率之后，就可以建立直方图直观地查看： 

泊松分布表示的是概率分布，因此计算的时候需要计算总概率，比如计算每天准备 8 个馒头，就是将 8 个馒头、7 个馒头一直到 1 个馒头的概率都加起来，显示是 93%。

因此每天准备 8 个馒头的话，能有 93%的概率保证不会缺货。

以上就是离散型分布中的三个常见分布类型，你要注意它们之间的区别。其中二项分布是指试验次数固定、求成功次数的概率；几何分布是指试验次数固定，求第 N 次试验会成功的概率；泊松分布是指固定时间内，某个事件会发生 N 次的概率。

连续型概率分布

跟离散概率分布相反，当数据之间是有联系、呈现一定规律的时候，而且事件之间不独立的概率就属于连续性概率。

比如计算时间概率分布，时间是连续的，你永远无法将时间进行拆解，第一秒与第二秒中间还存在着的数据不能细分，这种分布就属于连续型分布。

连续型分布最常见的代表就是正态分布：

正态分布是指越靠近中间取值的值越多，而越远离中间取值出现的次数越少，如全校同学的身高、平均每个月的开销等。

正态分布的平均值叫作 μ，它决定了中心点的位置，标准差 σ 决定数据的集中度。那么正态分布有什么用呢？

这时候就要涉及正态分布一个非常重要的性质：中心极限定理。也就是说，如果统计对象是大量独立的随机变量，那么这些变量的平均值分布就会趋向于正态分布，不管原来它们的概率分布是什么类型！

比如统计某地区人的身高，每个人的身高都是独立的随机事件，但是当统计量足够大的时候，这些数据的平均值分布就会呈现出正态分布

 假设检验

假设检验就是通过抽取样本数据，并且通过小概率反证法去验证整体假设。为了便于你理解，我们还是举上节课的例子。

如果统计学家现在有 100 个面包，我们怎么知道面包的重量大多数在 400g 左右呢？

我们首先做一个假设，这个假设代表我们心中最不想承认的可能，叫作无效假设。比如这里我们假设大多数的面包都在 380g 以上，因为模具的问题，可能会有 390g 的面包，也可能会有 410g 的面包，这是正常的数据，这些数据应该符合正态分布。

但是出现 380g 的面包应该是很小概率的事件，我们不妨以 380g 为阈值，先假设我们的假设是正确的，也就是说面包大多数都在 380g 以上。

那么随机抽取 20 个面包作为样本，看一下里面高于 380g 的面包有几个。假如有 10 个，那么概率就是 0.5，一般来说小于 0.05 就是小概率事件，那么显然这个假设是成立的。

但是如果抽取 10 个面包，里面高于 380g 的只有 1 个，那么概率就是 0.05。显然这是一个小概率事件，在一次研究中是不应该发生的，而现在发生了，可能是我们所做的假设有问题，有理由拒绝无效假设，也就是说面包大多数都不足 380g。

 

简言之，假设检验的核心思想是小概率反证法，即在假设的前提下，估算某事件发生的可能性，如果该事件是小概率事件，在一次研究中本来是不可能发生的，现在却发生了，这时候就可以推翻之前的假设，接受备择假设。如果该事件不是小概率事件，我们就找不到理由来推翻之前的假设，实际中可引申为接受所做的无效假设。

而一般假设检验会存在两种错误。

第一种：原假设是对的，但你拒绝了原假设，这种错误就叫作弃真错误，这个错误的概率也叫作显著性水平 α，或称为容忍度。通常为了控制第一类错误发生的概率，一般情况下 α 取值为 0.01、0.05、0.1 等。

比如你做的假设是“太阳每天从东方升起”，但是最终你拒绝了这个假设，得出结论“太阳从西方升起”，这就是弃真错误。

第二种：原假设是错的，但你承认了原假设，这种错误就叫作取伪错误，这个错误的概率我们记为 β。

 

比如你做的假设是“太阳每天从西方升起”，但是最终你承认了这个假设，这就是取伪错误。

那么我们怎么避免这两种错误呢？其实就是用什么标准去检验是否为小概率事件，这里就要提到假设检验中的检验标准：显著性水平 α、P 值。

显著性水平 α，我们刚才讲过了就是容忍度，也就是标明犯第一类错误的概率不超过 α；P 值就是当原假设为真时，所得到的是样本观察结果或更极端结果出现的概率。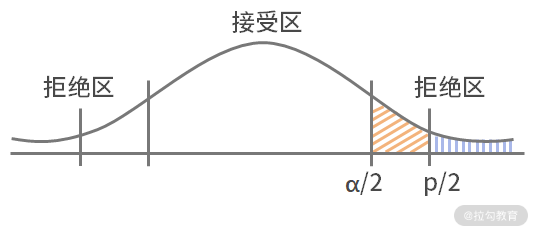

 

如果 P 值小于 α，说明原假设情况发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设。并且 P 值越小，我们拒绝原假设的理由越充分。总之，P 值越小，表明结果越显著。

假设检验的内容是我们后面学习统计学模型的基础，你需要认真地理解和消化这些概念的具体含义和使用方法，理解了之后你就会发现下一讲要介绍的回归模型就真的是无比简单了！