【博弈】非完全信息博弈基础与CFR算法简介

非完全信息博弈基础

0 非完全信息扩展式博弈

信息集：玩家无法区分的博弈状态集合，在这些状态下可选择的动作必须遵循同一分布。

有限的非完全信息扩展式博弈 $<N,H,P,f_c,I_i,u_i>$

• 参与者集合 $N$： N = { c , 1 , 2 , … , n } N=\{\mathrm{c}, 1,2, \ldots, \mathrm{n}\} N={c,1,2,…,n}，$c$ 为机会玩家，其余为普通玩家。
• 博弈状态集合 $H$：每个博弈状态 $h\in H$ 由动作的历史序列组成，即从根节点到当前决策节点的路径中经过的决策的序列（有序集）。在根节点处序列为空，ℎ的所有前缀序列也属于 $H$。$Z\subseteq H$​ 是博弈终止状态集合，代表博弈结束胜负已分。$A(h)=a:h.a\in H$ 为在非终止状态 $h\in H$ 处可供选择的合法动作集合，其中，$h.a$ 代表在 $h$ 状态处选择动作 $a$ 后能到达的状态。显然，在 $Z$ 处没有可选择的动作。
• 决策者函数 $P$：函数 $P$ 为每个非终止状态分配一个决策玩家。$P(h)=i$ 代表在博弈状态 $h$ 处做出决策的玩家为 $i$。如果 $P(h)=c$，此时在博弈状态 $h$ 处做出决策的玩家为机会玩家。
• 机会概率分布 $f_c$：如果状态 $h$ 处做出决策的玩家是机会玩家 $c$，那么 $c$ 选择的动作的概率分布服从于 $f_c$。
• 信息集 $I_i$：一个信息集是 $H$ 的子集，当其他玩家通过观测历史 $h$ 时，只知道玩家处于集合 $I$ 上，但是并不清楚该玩家具体在 $I$ 的哪一个状态上。每个玩家的所有信息集组成一个信息分割。对于每个玩家 $i\in N$ 都存在一个信息分割， I i = { I i ∣ I i ⊂ H , P ( I i ) = i } \mathcal{I}_{i}=\left\{I_{i}\right.\left.\mid I_{i} \subset H, P\left(I_{i}\right)=i\right\} Ii​={Ii​∣Ii​⊂H,P(Ii​)=i}。信息集 $I_i$ 中的状态 $h,h^{{}^{\prime }}\in I_i$ 是不可区分的，且有 $A(h)=A(h^{{}^{\prime }})$。
• 收益函数 ${\mu }_i$：对于玩家 $i\in N$，收益函数 ${\mu }_i:Z\to R$ 在终止状态 $Z$ 处根据结局输赢为玩家 { 1 , 2 , … , N } \{1,2, \ldots, N\} {1,2,…,N} 分配各自的收益。

1 博弈策略

在完全信息博弈中，策略是限制在博弈状态中的，它规定了在每个博弈状态下玩家选择合法动作的概率；在非完全信息博弈中，策略与信息集有关，玩家在不同信息集上进行决策。

定义：对于玩家 $i$ 来说，当他处于信息集 $I_i$ 时，他在动作集合 $A(I_i)$ 中选择的动作的概率分布遵循策略 ${\sigma }_i$。用 ${\sum }_i$ 来表示玩家 $i$ 的策略空间。一个策略组 $\sigma$ 包含了每个玩家的策略， σ = { σ 1 , σ 2 , … , σ n } \sigma = \left\{\sigma_{1}, \sigma_{2}, \ldots, \sigma_{n}\right\} σ={σ1​,σ2​,…,σn​}。 ${\sigma }_{-i}$ 表示策略组中除了策略 ${\sigma }_i$ 之外的所有策略。

令 ${\pi }^{\sigma }(h)$ 表示如果所有玩家根据策略组 Font metrics not found for font: . 来选择动作，能到达状态 $h$ 处的概率。可将 ${\pi }^{\sigma }(h)$ 分解为每个玩家对于能够到达状态 $h$ 处所做的贡献，即 π i σ ( h ) = ∏ i ∈ N ∪ { c } π i σ ( h ) \pi_{i}^{\sigma}(h)=\prod_{i \in N \cup\{c\}} \pi_{i}^{\sigma}(h) πiσ​(h)=∏i∈N∪{c}​πiσ​(h)。用 Font metrics not found for font: . 来表示当所有玩家都根据策略组 Font metrics not found for font: . 来行动时，在已经到达状态 $g$ 的前提下，到达状态 $h$ 处的概率。由此得到，玩家 $i$ 在依据策略组 Font metrics not found for font: . 来行动时，在终止节点处所得到的的整体收益为 $u_i(\sigma )={\sum }_{h\in Z}{u}_i(h){\pi }^{\sigma }(h)$。

平均策略：假定在 $T$ 次博弈过程中，参与者 $i$ 在第 $t$ 次博弈所使用的策略为 ${\sigma }_i^t$，那么平均策略 ${\bar{\sigma }}_i^T=\frac{1}{T}{\sum }_{t=1}^T{\sigma }_i^t$ 是策略 ${\sigma }_i^1,{\sigma }_i^2,\dots ,{\sigma }_i^T$ 在每个信息集 $I$ 上概率 ${\sigma }_i^t(I)$ 的简单加权平均。

最佳反应（best response，BR）策略：如果玩家 $i$ 的对手策略组保持不变，那么玩家 $i$ 可以在策略空间 ${\sum }_i$ 中寻找一个最大化自身收益的策略。给定一个策略组 $\sigma =\left({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n\right)$，${\mu }_i(\sigma )$ 表示在策略组 $\sigma$ 下参与者 $i$ 的期望收益，当对手策略组是 ${\sigma }_{-i}$ 时，参与者 $i$ 为应对 ${\sigma }_{-i}$ 所选择的最佳反应策略 $BR({\sigma }_{-i})$ 为：
$$BR\left({\sigma }_{-i}\right)={\mathrm{argmax}}_{{\sigma }_i^{\prime }}{u}_i\left({\sigma }_i^{\prime },{\sigma }_{-i}\right)$$
纳什均衡：对于所有博弈方而言，只要其他人不做出改变，那么每个博弈方都不可能通过改变己方当前所选择的策略，而达到比现在更高的收益目标。纳什均衡是当所有参与者的策略都是最佳反应策略时的策略组 ${\sigma }_i^{\ast }$：
$$\forall i,u_i\left({\sigma }_i^{\ast },{\sigma }_{-i}^{\ast }\right)=\underset{{\sigma }_i^{\prime }\in {\Sigma }_i}{\max }{u}_i\left({\sigma }_i^{\prime },{\sigma }_{-i}^{\ast }\right)$$
可利用度（Exploitability）：衡量某一个策略与纳什均衡策略的偏离程度。在二人零和博弈中，策略 ${\sigma }_i$ 的可利用度 $e({\sigma }_i)$ 指当对手的策略是最佳反应策略 $BR({\sigma }_{-i})$ 时，策略 ${\sigma }_i$ 跟纳什均衡策略相比，其劣势有多少：
$$e\left({\sigma }_i\right)=u_i\left({\sigma }_i^{\ast },BR\left({\sigma }_{-i}^{\ast }\right)\right)-u_i\left({\sigma }_i,BR\left({\sigma }_{-i}\right)\right)$$
一个策略组的平均可利用度为 $e(\sigma )/|N|$。若 $e(\sigma )/|N|<ϵ$，则称 $\sigma$ 为 $ϵ-纳什均衡$。

2 遗憾最小化与遗憾值匹配

根据对过去博弈中行为动作的遗憾程度来对将来动作进行选择

遗憾值：考虑 $T$ 次重复博弈，令 ${\sigma }_i^t$ 表示参与者 $i$ 在第 $t$ 次博弈过程中使用的策略，参与者 $i$ 在第 $T$ 次博弈后的 平均总体遗憾值 为：
$$R_i^T=\frac{1}{T}\underset{{\sigma }_i^{\ast }\in {\Sigma }_i}{\max }\sum _{t=1}^T\left(u_i\left({\sigma }_i^{\ast },{\sigma }_{-i}^t\right)-u_i\left({\sigma }_t\right)\right)$$
上式中，$u$ 为收益函数。单次博弈的遗憾值是最佳应对策略与实际策略的收益的差值，它反应了没有采取最佳应对策略的遗憾程度。令 $R_i^{T,+}=\max \left(0,{\mathrm{R}}_i^T\right)$，随着博弈次数 $T$ 趋近于无穷大，若 $R_i^{T,+}$ 趋近于0，称之为 遗憾值最小化。

当一个算法通过选择策略 ${\sigma }_i^t$ 使得参与者的平均总体遗憾值随着博弈次数 $T$ 的增长而趋近于 0 时，称该算法为遗憾值最小化算法。在二人零和扩展式博弈问题中，使用遗憾值最小化算法并进行自我博弈，最终可以求解出近似的纳什均衡。

遗憾值匹配：正则博弈中的遗憾匹配是使遗憾最小化的简单的迭代过程。首先，我们随机选择策略 ${\sigma }^1$，对于可选动作集 $A_i$ 中的每一个动作 $a$，我们计算并存储其遗憾值：
$$R_i^T(a)=\sum _{t=1}^T\left({\mu }_i\left(a,{\sigma }_{-i}^t\right)-{\mu }_i\left({\sigma }_i^t,{\sigma }_{-i}^t\right)\right)$$
下一次迭代时候，我们采取的策略通过下式计算出：
$${\sigma }_i^{T+1}(a)=\frac{R_i^{T,+}(a)}{{\sum }_{b\in A_i}{R}_i^{T,+}(b)}$$
当分母为0时，随机选择下一个动作。最直观的理解就是我们会选择过去最让自己感到遗憾（后悔没有选的）动作。遗憾值匹配算法的流程图：

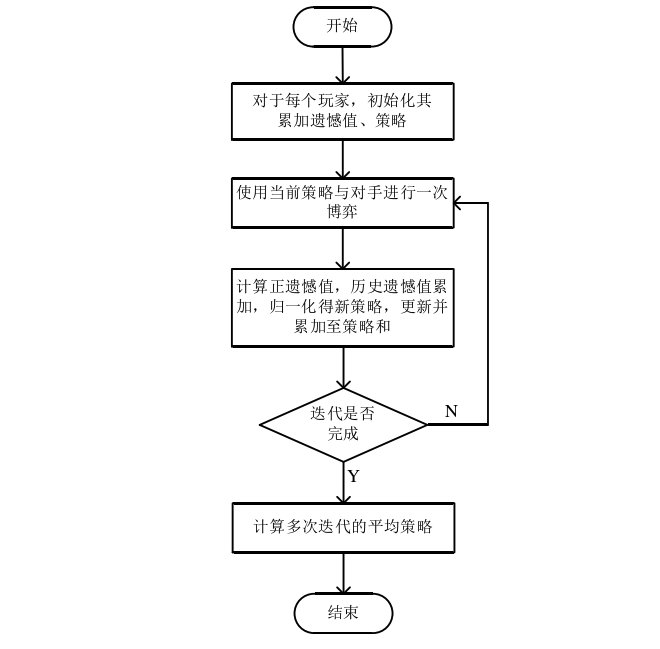
遗憾值最小化技术是通过计算平均 整体 最小遗憾（average overall regret）得到游戏中的行为策略，因此该技术 只致力于解决正则博弈游戏。在扩展式博弈游戏中，游戏状态是呈指数增长的，如最简单的2人限制性德州扑克扩展式游戏，都有着多达 $10^{17}$ 的游戏状态。首先要计算如此规模博弈树的整体最小遗憾是不切实际的，而且扩展式博弈是按次序做动作的，因而通过遗憾值最小化技术不能立即得到下一动作的可选策略。所以在扩展式博弈中Martin Zinkevich等人引进了虚拟遗憾（counterfactual regret）的概念。

3 虚拟遗憾最小化（CFR）

反事实遗憾，即虚拟遗憾，指故意地使玩家 $i$ 的策略被限定在信息集 $I_i$。CFR 算法通过多次迭代，将整体遗憾分解到各个独立的信息集中计算局部最小遗憾值。CFR 算法的形式化定义如下：

$Z$ 表示博弈树中所有的叶子结点，$z\in Z$，$h$ 表示博弈树中的非叶子结点，${\mu }_i(z)$ 表示玩家 $i$ 在叶子结点 $z$ 的效用。定义在非叶子节点 $h$ 处的 虚拟价值（counterfacter value）：
$$v_i(\sigma ,h)=\sum _{z\in Z,h\notin z}{\pi }_{-i}^{\sigma }(h){\pi }^{\sigma }(h,z)u_i(z)$$
在节点 $h$ 处采用动作 $a$ 的 虚拟遗憾值（counterfactual regret）：
$$r(h,a)=v_i\left({\sigma }_{I\to a},h\right)-v_i(\sigma ,h)$$
在信息集 $I$ 处采取动作 $a$ 的虚拟遗憾值：
$$r(I,a)=\sum _{h\in I}r(h,a)$$
在 $T$ 次迭代中累加的虚拟遗憾值：
$$R_i^T(I,a)=\sum _{t=1}^T{r}_i^t(I,a)$$
则对于信息集 $I_i$，通过遗憾匹配得到当前的策略：
$${\sigma }_i^{T+1}(I,a)=\{\begin{array}{cc}\frac{R_i^{T,+}(I,a)}{{\sum }_{a\in A(I)}{R}_i^{T,+}(I,a)}& \text{ if }{\sum }_{a\in A(I)}{R}_i^{T,+}(I,a)>0\\ \frac{1}{|A(I)|}& \text{ otherwise. }\end{array}$$
CFR 通过一次迭代，在被访问到的每个信息集上计算虚拟价值和虚拟遗憾值，当下一次迭代开始时，将会带入上次迭代的结果通过遗憾匹配计算新的策略。