本文主要是介绍挖掘商品关联性(2): FP-growth算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
从这个贸易战看:强权即是真理,没有所谓的自由贸易和平等。中国之大已容不下一个安静的键盘。不过是又一次鸦片战争。除了愤怒还是愤怒,除了一心想为崛起而澎湃还是一心想为崛起而澎湃。中华文明三四千年的历史都是世界顶级,美国人区区100多年第一就想再占100年这不是无知么?中国人有13亿人,是美国人的4倍还要多,4个抵1个也是必然会超过美国。
2019年5月29日 IEEE宣布禁止任何受华为资助的教授或学生参与IEEE审稿。听到这个消息我是愤怒的,说好的科学无国界呢?
梳理下这个过程:
2018.12.1,华为CFO(任正非之女)被美国下令逮捕
2018.12.1 对芯片重大贡献的华人张首晟在美国身亡,就在2年前获得中国国家科学技术奖(中国科技最高奖,最高领导人亲自颁奖,奖金200万美金)
2019年5月 美国撕毁两国元首已经基本确定的协议,对中国征收25%关税。
2019年5月中旬 美国禁止全世界任何企业与华为接触或者提供设备,也禁止购买华为手机或通讯设备。理由:“国家安全”(距离美国棱镜门用思科通讯设备和Google监听全世界这个事件不过几年美国人就忘了自己干了什么事。)同时禁止欧洲其他国家使用华为提供的5G服务。
2019年5月中下旬,Microsoft,ARM,Google纷纷宣布停止和华为任何商业来往,同时Google禁止华为手机使用Google服务。
2019年5月底, IEEE(世界上最大电子电气学术机构)禁止任何受华为资助的教授参与审稿。禁止其他高校或企业与中国的一些高校合作。
1. 背景
在前面我们介绍了一种简单的挖掘商品关联性算法Apriori算法。今天要介绍的是更高效的FP-growth算法(FP指的是Frequent Pattern),它可以用到搜索词提醒,常用词,挖掘强关联性商品,商品推荐等领域上。挖掘商品关联系或者词语之间的关联性,需要做的事是构造各种商品组合然后分析出这种组合是否是高频率出现。Apriori算法每产生一种组合都要遍历一次数据库来判断当前组合是否是高频记录(如果你对这句话不理解建议看下这篇文章:易懂机器学习Apriori算法商品关联性分析)。这个在大量数据面前是很耗时间。。
2. FP-growth执行过程
初衷:现在我们需要做的事是构造各种商品组合然后分析出这种组合是否是高频率出现。由于Apriori算法每次构造出一种组合都要遍历一遍数据集来统计当前这种组合出现次数这个耗费时间过大。那我们能不能把数据集压缩呢?假设是账单数据集。那么肯定会有很多账单会有大量公共商品组合。如果我们把这些公共商品作为前缀,那么就能压缩数据集。压缩数据集的好处就是可以减少我们统计某种组合出现次数所花费的时间。FP-growth算法就是这么做的,它数据构造成一颗树。相同商品在上层节点,并且每个节点记录了当前节点重复利用次数,以方便统计出现频率。
还是拿这个举例子:
{啤酒 鸡蛋 尿布 西红柿}
{香烟 尿布 鸡蛋 啤酒 }
{土豆 西红柿 洋葱 醋 鸡蛋}
先将它们编号:
[1]啤酒 [2]鸡蛋 [3]尿布 [4]西红柿 [5]香烟 [6]土豆 [7]洋葱 [8]醋
上面这个数据集用编号表示就是
[
[1, 2, 3, 4],
[5, 3, 2, 1],
[6,4,7,8, 2]
]
- 和Apriori算法一样。先设定一个阈值,出现频率超过这个阈值就认为是高频率。算频率有点麻烦,这里我们认为超过2次就是高频率吧。
- 和Apriori算法一样统计各个商品的出现次数,剔除低频率商品。
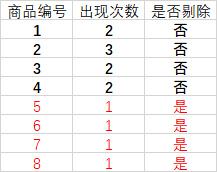
- 从这一步开始与Apriori算法不一样了。根据频率将每条账单内的商品按频率排序(并且剔除低频率商品)。
[
[2,1, 3,4],
[2, 1, 3],
[2,4]
]
3. FP树如何构造
- 根据上面那个排序好并且筛选过的逐个账单构造一棵树。节点格式:{物品编号}-节点重复经过次数
加入第一个账单
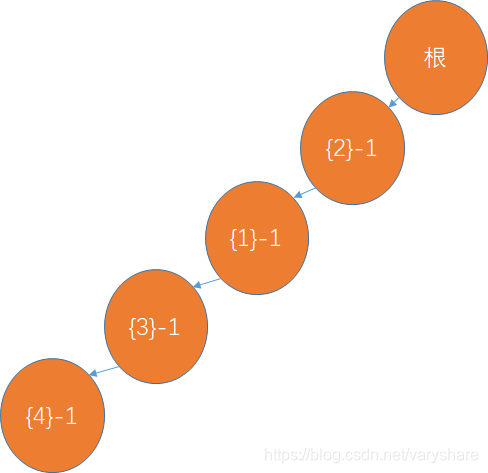
加入第二个账单:(与第一个账单前缀重合,所以重复利用节点,相关节点利用次数+1)
这篇关于挖掘商品关联性(2): FP-growth算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







