本文主要是介绍Kaggle|Give Me Some Credit信用卡评分建模分析(R语言),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.目的
本文是基于Kaggle|Give Me Some Credit项目(数据地址:https://www.kaggle.com/c/GiveMeSomeCredit),通过对消费者的人口特征、信用历史记录、交易记录等大量数据进行系统的分析、挖掘数据蕴含的行为模式、信用特征,发展出预测行的模式,结合信用卡评分的构建原理,采用R语言完成数据的清洗,主要包括缺失数据的填充、异常的删除和数据的分箱;调用Logistic回归模型建立信用卡评分的基础模型,借助自变量的证据权重转换(WOE)创建信用卡评分卡,并开发一个简单的信用评分系统。
2.背景
信用评分卡模型在国外是一种成熟的预测方法,尤其在信用风险评估以及金融风险控制领域更是得到了比较广泛的使用,其原理是将模型变量WOE编码方式离散化之后运用logistic回归模型进行的一种二分类变量的广义线性模型。
客户申请评分卡由一系列特征项组成,每个特征项相当于申请表上的一个问题(例如,年龄、银行流水、收入等)。每一个特征项都有一系列可能的属性,相当于每一个问题的一系列可能答案(例如,对于年龄这个问题,答案可能就有30岁以下、30到45等)。在开发评分卡系统模型中,先确定属性与申请人未来信用表现之间的相互关系,然后给属性分配适当的分数权重,分配的分数权重要反映这种相互关系。分数权重越大,说明该属性表示的信用表现越好。一个申请的得分是其属性分值的简单求和。如果申请人的信用评分大于等于金融放款机构所设定的界限分数,此申请处于可接受的风险水平并将被批准;低于界限分数的申请人将被拒绝或给予标示以便进一步审查。
3.数据处理
3.1数据说明
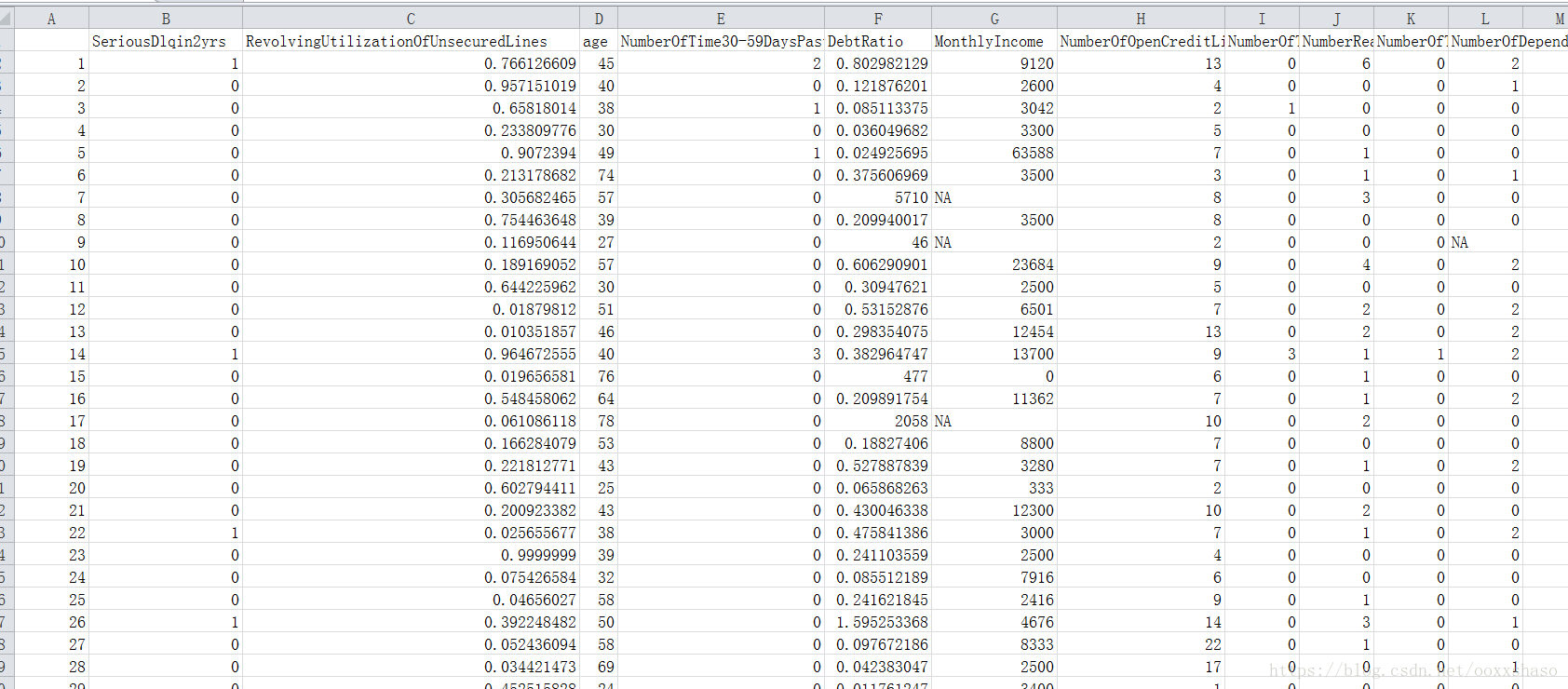
数据来自Kaggle的give me some credit项目,其中cs-training.csv是有15万条的样本数据,包含了12个变量,大致情况如下:
每个变量的解释如下:
SeriousDlqin2yrs:超过90天或更糟的逾期拖欠
RevolvingUtilization Of UnsecuredLines:无担保放款的循环利用:除了不动产和像车 贷那样除以信用额度总和的无分期付款债务的信用卡和个人信用额度总额
Age:借款人年龄
NumberOfTime30-59DaysPastDueNotWorse:30-59天逾期次数
DebtRatio:负债比例
MonthlyIncome:月收入
Number Of OpenCreditLinesAndLoans:贷款数量NumberOfTimes90DaysLate:90天逾期次数:借款者有90天或更高逾期的次数
NumberReal Estate Loans Or Lines:不动产贷款或额度数量:抵押贷款和不动产放款包括房屋净值信贷额度
Number Of Time 60-89Days PastDue Not Worse:60-89天逾期次数NumberOfDependents:家属数量,不包括本人在内的家属数量
3.2导入数据
setwd('E:/data for give me some credit')credit_data <- read.csv('cs-training.csv',stringsAsFactors = FALSE)
str(credit_data) #显示数据结构
'data.frame': 150000 obs. of 12 variables:$ X : int 1 2 3 4 5 6 7 8 9 10 ...$ SeriousDlqin2yrs : int 1 0 0 0 0 0 0 0 0 0 ...$ RevolvingUtilizationOfUnsecuredLines: num 0.766 0.957 0.658 0.234 0.907 ...$ age : int 45 40 38 30 49 74 57 39 27 57 ...$ NumberOfTime30.59DaysPastDueNotWorse: int 2 0 1 0 1 0 0 0 0 0 ...$ DebtRatio : num 0.803 0.1219 0.0851 0.036 0.0249 ...$ MonthlyIncome : int 9120 2600 3042 3300 63588 3500 NA 3500 NA 23684 ...$ NumberOfOpenCreditLinesAndLoans : int 13 4 2 5 7 3 8 8 2 9 ...$ NumberOfTimes90DaysLate : int 0 0 1 0 0 0 0 0 0 0 ...$ NumberRealEstateLoansOrLines : int 6 0 0 0 1 1 3 0 0 4 ...$ NumberOfTime60.89DaysPastDueNotWorse: int 0 0 0 0 0 0 0 0 0 0 ...$ NumberOfDependents : int 2 1 0 0 0 1 0 0 NA 2 ...3.3更换变量名
第一列为数据的索引,没什么意义,因此可以去除,需要预测的变量是SeriousDlqin2yrs,所以将这个变量重命名为y,其余变量重命名为x1~x10
> cr_data <- credit_data[,2:12]
> names(cr_data) <- c('y','x1','x2','x3','x4','x5','x6','x7','x8','x9','x10')
> head(cr_data)y x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
1 1 0.7661266 45 2 0.80298213 9120 13 0 6 0 2
2 0 0.9571510 40 0 0.12187620 2600 4 0 0 0 1
3 0 0.6581801 38 1 0.08511338 3042 2 1 0 0 0
4 0 0.2338098 30 0 0.03604968 3300 5 0 0 0 0
5 0 0.9072394 49 1 0.02492570 63588 7 0 1 0 0
6 0 0.2131787 74 0 0.37560697 3500 3 0 1 0 1cr_data$y <- 1-cr_data$y #0表示违约,1表示不违约3.4处理缺失值
这里需要用到VIM包和mice包,首先识别出缺失数据,VIM包中的matrixplot函数可以将数据集中的缺失数据以可视化的方式显示出来,在本例中红色表示缺失值,颜色越深表示缺失值越多,然后再用mice包中的mice.pattern()函数生成一个数据框来展示缺失值的个数.我自己的电脑VIM打死也没安装成功,暂时不演示如何用图表去看缺失值了,代码就是matrixplot(cr_data).
从图中可以看到x5变量(月收入)缺失值为29731个,x10(家属数量)缺失值为3924个
> library(lattice)
> library(mice)
> md.pattern(cr_data)y x1 x2 x3 x4 x6 x7 x8 x9 x10 x5
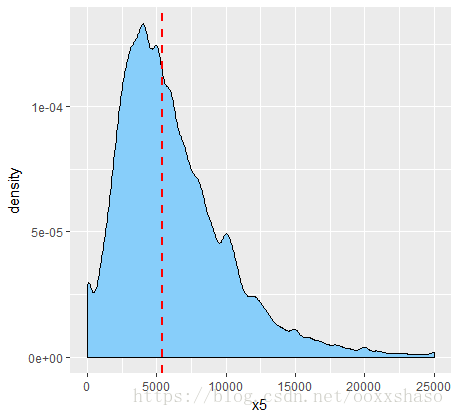
120269 1 1 1 1 1 1 1 1 1 1 1 025807 1 1 1 1 1 1 1 1 1 1 0 13924 1 1 1 1 1 1 1 1 1 0 0 20 0 0 0 0 0 0 0 0 3924 29731 33655可以看到x5的缺失值较多,直接删除可能会影响结果,可以采用中位数/均值/众数等方式填充缺失数据,由于x5呈明显的正态分布,因此用中位数去填充x5的缺失数据
> library(ggplot2)
> #x5(月收入)的概率密度图
> ggplot(data = cr_data,aes(x5))+geom_density(fill="lightskyblue")+xlim(0,25000)+geom_vline(aes(xintercept=median(cr_data$x5[!is.na(cr_data$x5)])),colour="red",linetype="dashed",lwd=1)
> #中位数填充x5缺失值
>cr_data$x5[is.na(cr_data$x5)]=median(cr_data$x5[!is.na(cr_data$x5)])#x10的缺失值数量所占比列较小,因此,直接将缺失值删除
> cr_data <- na.omit(cr_data)3.5处理异常值
关于异常值的检测,常见的检测方法有:
(1)单变量异常值检测:调用R语言中的boxplot.stats()函数可以实现单变量异常值的检测,该函数基于数据生成的箱体图进行异常值的检测。在函数的返回结果中,参数out是由异常值组成的列表。
(2)使用LOF(local outlier factor,局部异常因子)进行异常值检测:LOF(局部异常因子)是用于识别基于密度的局部异常值的算法。使用LOF,一个点的局部密度会与它的邻居进行比较。如果前者明显低于后者(有一个大于1 的LOF值),该点位于一个稀疏区域,对于它的邻居而言,这就表明,该点是一个异常值。LOF的缺点就是它只对数值数据有效。R语言中DMwR和dprep包的lofactor()函数使用LOF算法计算局部异常因子。
(3)聚类进行异常值的检测:通过把数据聚成类,将那些不属于任务一类的数据作为异常值。比如,使用k-means算法来检测异常。使用k-means算法,数据被分成k组,通过把它们分配到最近的聚类中心。然后,我们能够计算每个对象到聚类中心的距离(或相似性),并且选择最大的距离作为异常值。
3.5.1 处理age异常值
> boxplot(cr_data$x2)结合现实中的信用卡申请条件,申请人的年龄必须在18~65岁之间,因此将小于18和大于65的数据进行删除,并用boxplot.stats()检查删除后的异常值为0
> cr_data <- cr_data[cr_data$x2 <= 65 & cr_data$x2 >= 18,]
> boxplot.stats(cr_data$x2)
$`stats`
[1] 21 39 48 56 65$n
[1] 119063$conf
[1] 47.92216 48.07784$out
integer(0)3.5.2 处理x3,x7,x9的异常值
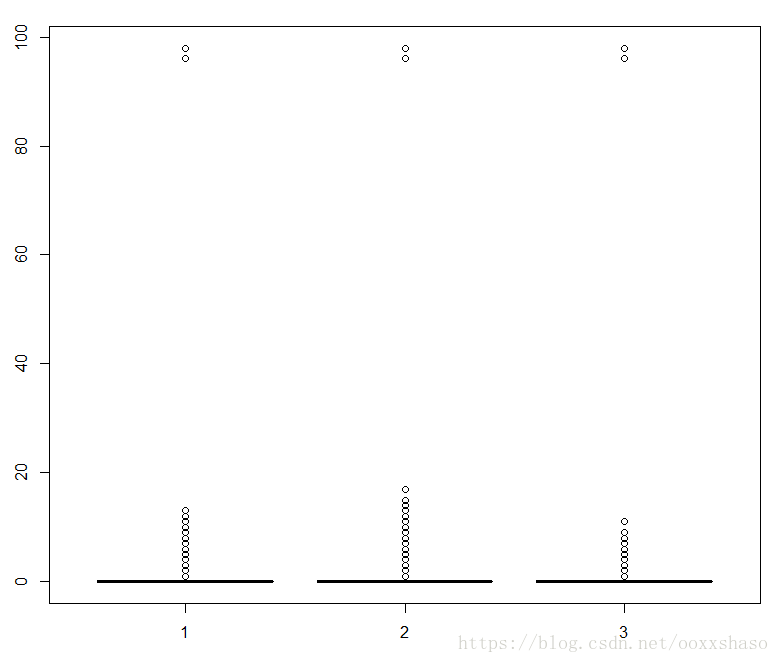
> boxplot(cr_data$x3,cr_data$x7,cr_data$x9)可以看到异常值均为接近100的值,均删除.
> boxplot(cr_data$x3,cr_data$x7,cr_data$x9)
> unique(cr_data$x3)[1] 2 0 1 3 4 5 7 10 6 98 12 8 9 96 13 11
> unique(cr_data$x7)[1] 0 1 3 2 5 4 98 10 9 6 7 8 15 96 11 13 14 17 12
> unique(cr_data$x9)[1] 0 1 2 5 3 98 4 6 7 8 96 11 9
> cr_data <- cr_data[-which(cr_data$x3==96),]
> cr_data <- cr_data[-which(cr_data$x3==98),]
> unique(cr_data$x7)[1] 0 1 3 2 5 4 10 9 6 7 8 15 11 13 14 17 12
> unique(cr_data$x9)[1] 0 1 2 5 3 4 6 7 8 11 9
> #可以看出已无异常值4.建模分析
4.1 变量的相关性分析
建模之前需要先检验变量之间的相关性,,如果变量之间具有强相关性,则会影响模型的准确性.调用R中的cor()函数来计算不同变量之间的相关系数,同时,调用corrplot包中的corrplot()函数来将相关系数可视化
> library(corrplot)
corrplot 0.84 loaded
> cor1 <- cor(cr_data)
> corrplot(cor1,method = 'number')
由上图可知:各个变量之间的相关系数较小,相关性较弱,不存在明显的多重共线问题,采用logistic回归需要考虑多重共线问题,在此处由于个变量之间的相关性较小,可以初步判断不存在多重共线问题.在建模之后也可以通过VIF(方差膨胀因子)来检验多重共线问题.当存在多维共线问题时,需要进行降维或剔除处理.
4.2 切分数据集
> table(cr_data$y)0 1 9044 109785 由上表可知:响应变量y存在着明显的类失衡问题,y等于0的观测值为9044,仅占所有观测值的7.6%,因此,我们需要对非平衡数据进行处理,基于smote算法,调用R语言中caret包中的createDataPartition对稀有数据进行超级采样。
> library(caret)
> set.seed(500)
> splitindex <- createDataPartition(cr_data$y,times = 1,p=0.5,list = FALSE)
> traindata <- cr_data[splitindex,]
> testdata <- cr_data[-splitindex,]> prop.table(table(traindata$y))0 1
0.0771354 0.9228646 > prop.table(table(testdata$y))0 1
0.07508331 0.92491669 由上表可知:两者分类后的结果是平衡的,y等于1的概率均为7.6%左右,处于良好的水平,因此,可以采用切割后的数据进行建模和预测分析。
4.3建模分析
Logistic回归模型在信用卡评分开发的基础模型,由于其自身的特点以及对自变量进行证据权重转换(WOE),logistic回归的结果可以直接转换为一个汇总表,即所谓的标准评分卡格式。调用R语言中glm()函数对所有变量进行logistic回归建模.
> fit=glm(y~.,data=traindata,family = "binomial")
Warning message:
glm.fit:拟合機率算出来是数值零或一
> summary(fit)Call:
glm(formula = y ~ ., family = "binomial", data = traindata)Deviance Residuals: Min 1Q Median 3Q Max
-5.2021 0.2552 0.3014 0.3581 4.4247 Coefficients:Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.769e+00 7.395e-02 23.919 < 2e-16 ***
x1 -6.035e-06 7.113e-05 -0.085 0.93239
x2 2.466e-02 1.668e-03 14.785 < 2e-16 ***
x3 -5.599e-01 1.628e-02 -34.399 < 2e-16 ***
x4 5.078e-05 1.778e-05 2.856 0.00429 **
x5 4.136e-05 5.055e-06 8.181 2.81e-16 ***
x6 8.239e-03 4.079e-03 2.020 0.04339 *
x7 -8.260e-01 2.462e-02 -33.550 < 2e-16 ***
x8 -1.148e-01 1.663e-02 -6.899 5.23e-12 ***
x9 -7.321e-01 3.339e-02 -21.927 < 2e-16 ***
x10 -5.823e-02 1.394e-02 -4.176 2.96e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for binomial family taken to be 1)Null deviance: 32288 on 59414 degrees of freedom
Residual deviance: 26558 on 59404 degrees of freedom
AIC: 26580Number of Fisher Scoring iterations: 6由上述结果可知,变量x1,x4,x6对响应变量y的贡献不显著,因此直接删除这三个变量,利用剩下的变量来进行logistic回归
> fit2 <- glm(y~x2+x3+x5+x7+x8+x9+x10,data=traindata,family = "binomial")
Warning message:
glm.fit:拟合機率算出来是数值零或一
> summary(fit2)Call:
glm(formula = y ~ x2 + x3 + x5 + x7 + x8 + x9 + x10, family = "binomial", data = traindata)Deviance Residuals: Min 1Q Median 3Q Max
-5.1559 0.2554 0.3019 0.3583 4.4472 Coefficients:Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.786e+00 7.358e-02 24.278 < 2e-16 ***
x2 2.578e-02 1.633e-03 15.788 < 2e-16 ***
x3 -5.551e-01 1.609e-02 -34.497 < 2e-16 ***
x5 4.037e-05 4.976e-06 8.114 4.91e-16 ***
x7 -8.352e-01 2.435e-02 -34.294 < 2e-16 ***
x8 -9.317e-02 1.532e-02 -6.081 1.19e-09 ***
x9 -7.341e-01 3.342e-02 -21.967 < 2e-16 ***
x10 -6.084e-02 1.388e-02 -4.383 1.17e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for binomial family taken to be 1)Null deviance: 32288 on 59414 degrees of freedom
Residual deviance: 26571 on 59407 degrees of freedom
AIC: 26587Number of Fisher Scoring iterations: 6
4.4 模型评估
通常一个二值分类器可以通过ROC曲线和AUC值进行评价,由于很多二元分类器会产生一个概率值,而非仅仅的0~1预测值。我们可以使用临界点,当概率预测值大于该临界点时,划分为1,概率预测值小于该临界点时,划分为0。得到二元预测值后,可以构建一个混淆矩阵来评价二元分类器的预测效果。所有的训练数据都会落入这个矩阵中,而对角线上的数字代表了预测正确的数目,即true positive + true nagetive。同时,计算出TPR(真正率或称为灵敏度)和TNR(真负率或称为特异度),其中,伪阳性率(FPR)=1-TNR。除了分类器的训练参数,临界点的选择,也会大大的影响TPR和TNR。有时可以根据具体问题和需要,来选择具体的临界点。
如果我们选择一系列的临界点,就会得到一系列的TPR和TNR,将这些值对应的点连接起来,就构成了ROC曲线。ROC曲线可以帮助我们清楚的了解到这个分类器的性能表现,还能方便比较不同分类器的性能。在绘制ROC曲线的时候,习惯上是使用1-TNR作为横坐标即FPR(false positive rate),TPR作为纵坐标。这是就形成了ROC曲线。
而AUC(Area Under Curve)被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
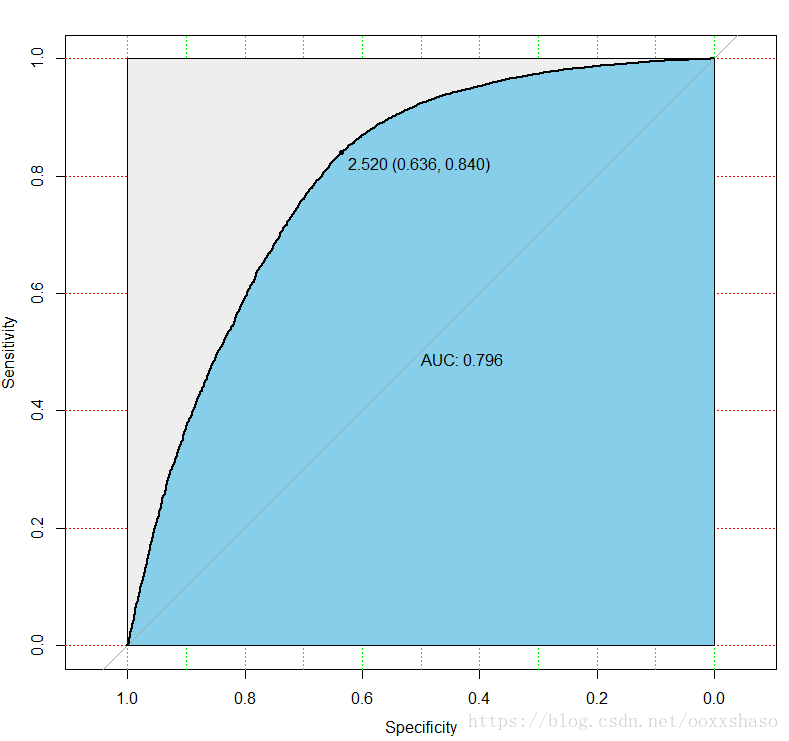
调用R语言中pROC包中的roc函数计算分类器的AUC值,可以方便的比较两个分类器,并且自动标注出最优的临界点。如下图所示:最优点FPR=1-TNR=0.840,TPR=0.636,AUC值为0.796,说明该模型的预测效果不错,正确率较高。
> pre=predict(fit2,testdata)
> library(pROC)
Type 'citation("pROC")' for a citation.载入程辑包:‘pROC’The following objects are masked from ‘package:stats’:cov, smooth, var> modelroc=roc(testdata$y,pre)
> plot(modelroc, print.auc=TRUE, auc.polygon=TRUE, grid=c(0.1, 0.2),
+ grid.col=c("green", "red"), max.auc.polygon=TRUE,auc.polygon.col="skyblue", print.thres=TRUE)5.WOE转换
证据权重(Weight of Evidence,WOE)转换可以将Logistic回归模型转化为标准评分卡格式,引入WOE转换的目的并不是为了提高模型质量,而是由于一些变量不应该被纳入模型,或者是因为它们不能增加模型值,或者是因为与其模型相关系数有关的误差较大,其实建立标准信用评分卡也可以不采用WOE转换。这种情况下,Logistic回归模型需要处理更大数量的自变量。尽管这样会增加建模程序的复杂性,但最终得到的评分卡都是一样的。
用WOE(x)替换变量x,WOE()=ln[(违约/总违约)/(正常/总正常)]。由于模型中剔除x1,x4,x6三个变量,因此对剩下的变量进行WOE转换。
5.1 数据分箱
WOE分箱原则:
1.分箱数量适中,不宜过多和过少。
2.各个分箱内的记录数应该合理,不应过多或者或过少。
3.结合目标变量,分箱应该表现出明显的趋势。
4.相邻分箱的目标变量分布差异尽可能大。
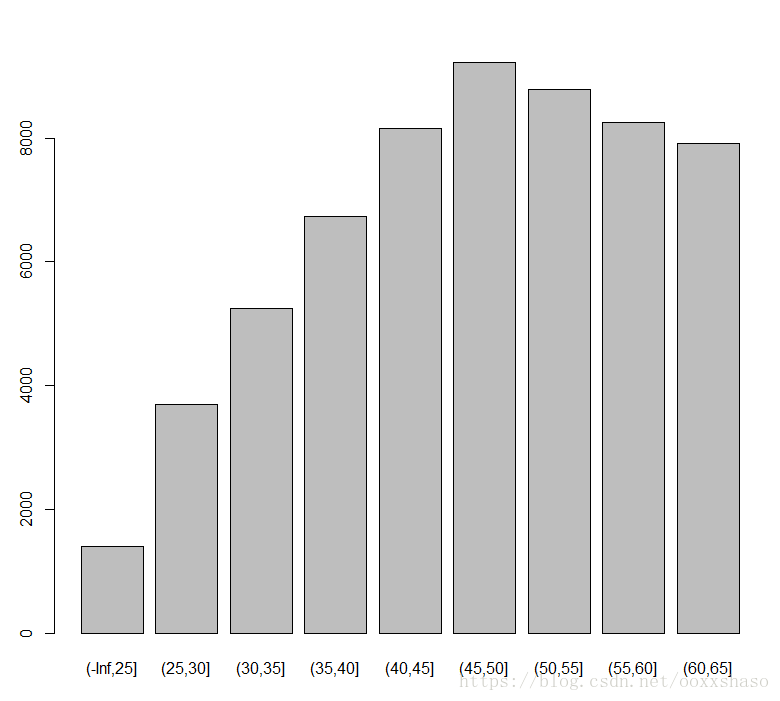
x2变量(age分箱)
> cutx2=c(-Inf,25,30,35,40,45,50,55,60,65)
> plot(cut(traindata$x2,cutx2))x3变量分箱
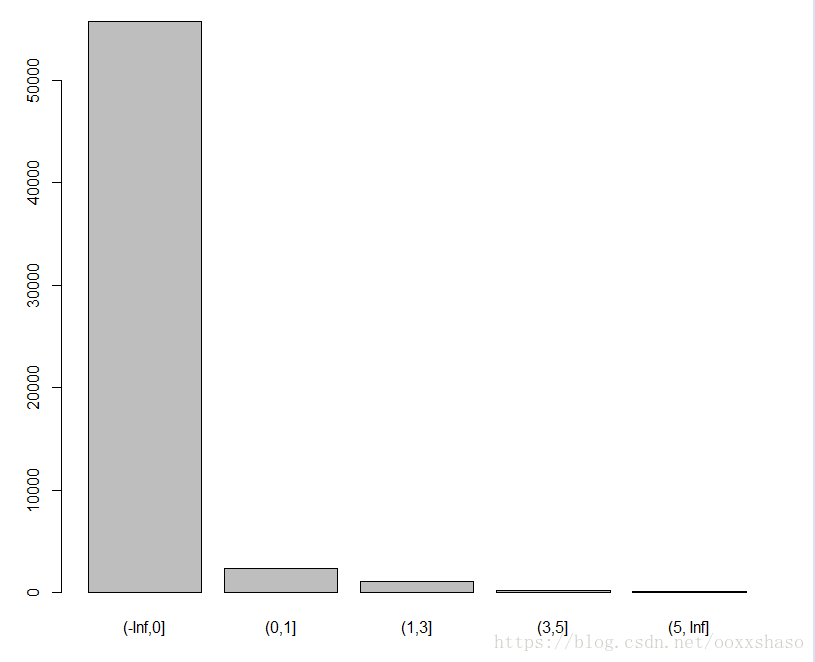
> cutx3=c(-Inf,0,1,3,5,Inf)
> plot(cut(traindata$x3,cutx3))x5变量分箱
> cutx5=c(-Inf,2000,3000,4000,5000,6000,7500,9500,12000,Inf)
> plot(cut(traindata$x5,cutx5))x7变量分箱
> cutx7=c(-Inf,0,1,3,5,Inf)
> plot(cut(traindata$x7,cutx7))x8分箱
> cutx8= c(-Inf,0,1,2,3,5,Inf)
> plot(cut(traindata$x8,cutx8))
x9分箱
> cutx9 = c(-Inf,0,1,3,5,Inf)
> plot(cut(traindata$x9,cutx9))
x10分箱
> cutx10 = c(-Inf,0,1,2,3,5,Inf)
> plot(cut(traindata$x10,cutx10))5.2WOE数值计算
> #x2的WOE值
> agelessthan30=getwoe(traindata$x2,-Inf,30)
> age30to40=getwoe(traindata$x2,30,40)
> age40to50=getwoe(traindata$x2,40,50)
> age50to60=getwoe(traindata$x2,50,60)
> age60to65=getwoe(traindata$x2,60,65)
> age.woe=c(agelessthan30,age30to40,age40to50,age50to60,age60to65)
> age.woe
[1] 0.43555387 0.27427494 0.06637011 -0.20620943 -0.74500267同理,计算出其他变量的WOE值,分别如下:
> x3_woe
[1] -0.5207976 0.8374273 1.6003370 2.2152915 2.7804131
> x5_woe
[1] 0.22048191 0.38990261 0.37583957 0.18627954 -0.02563007 -0.15179000 -0.44092717
[8] -0.54503261 -0.51895581
> x7_woe
[1] -0.3789825 1.8726850 2.5803602 3.0893005
> x8_woe
[1] 0.3073539 -0.2468977 -0.2640414 -0.1193822 0.3895990 1.0255582
> x9_woe
[1] -0.2714009 1.6945721 2.6061341 2.9212868 3.3982109
> x10_woe
[1] -0.09893059 0.06819497 0.07729239 0.15846434 0.28712719 0.52653127
待续。。。
这篇关于Kaggle|Give Me Some Credit信用卡评分建模分析(R语言)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!