本文主要是介绍通过在Z平面放置零极点的来设计数字滤波器,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章来源地址:https://www.yii666.com/blog/393376.html
通过在Z平面放置零极点的来设计数字滤波器
要求:设计一款高通滤波器,用在音频信号处理过程中,滤掉100Hz以下的信号。
实现方法:通过在Z平面放置零极点的来设计数字滤波器。
设计要点:单位圆上对应于需要加强频率的点附近放置极点,即w=π处附近落极点,需要拉低的频点附近放置零点,即w=0处附近落零点。为了滤波器的稳定,所有极点必须在单位圆内,而零点可以在任何位置。为了使滤波器系数是实数,所有的复数值的极点和零点必须以共轭的形式出现。
设计过程中需解决的问题:
-
模拟信号频率变量F(或Ω)和离散时间信号的频率变量f(或ω)之间的关系为:f = F/Fs ; 其中Fs为采样频率。因此若设计截止频率为100Hz的高通滤波器,采样频率16KHz时,则其在Z平面的对应值为π/80≈0.04。网址:yii666.com
-
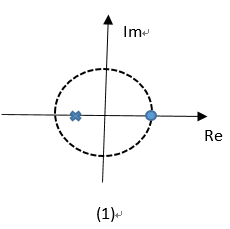
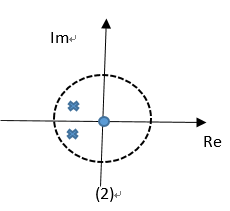
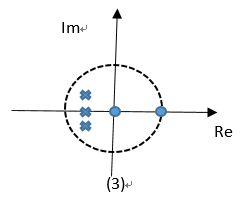
简单高通滤波器的零极点位置有以下几种形式:(1)单极点单零点(2)双极点单零点(3)多极点多零点。为了降低滤波器频率特性对误差的敏感程度,不采用单极点、单零点的方式,因此选用方式3进行高通滤波器的设计。
-
滤波器在Z域由零极点表示的表达式如下:
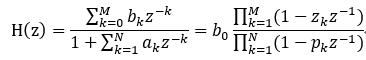
其中,z=e^jw
高通滤波器的幅频曲线中,w=0处,H(w)=0;w=π处,H(w)=1;
初步假设高通滤波器所具有三个极点和两个零点:
z1=0;z2=1;p1=-√3/2;p2=-√3/2+j1/2;p2=-√3/2-j1/2。
将各零极点值带入到H(z)表达式中,并根据w=π时H(w)=1,可得出b0的值,再将H(z)写成多项式的形式,如下:
此时,该多项式对应的时域差分方程为: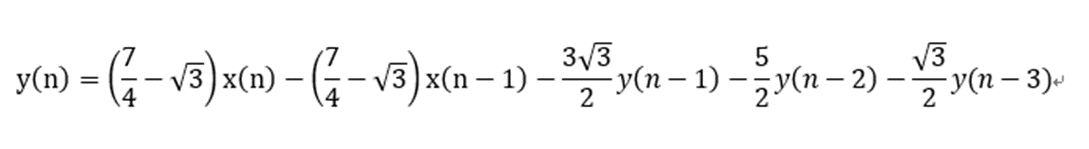
至此,该高通滤波器设计初步完成,但是并未使用到截止频率的相关信息,并且需使用matlab进行频域信息的验证,后续再进行探究。待验证完成后,便可添加到音频处理过程中,进行低频信号的过滤。
文章来源地址:https://www.yii666.com/blog/393376.html
基于matlab的零极点累试法滤波器设计 - 道客巴巴 (doc88.com)
这篇关于通过在Z平面放置零极点的来设计数字滤波器的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





