本文主要是介绍递归特征消除(Recursive Feature Elimination)原理与Sklearn实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
递归特征消除(Recursive Feature Elimination)
参考:
- Guyon, I., Weston, J., Barnhill, S., & Vapnik, V., “Gene selection for cancer classification using support vector machines”, Mach. Learn., 46(1-3), 389–422, 2002. https://link.springer.com/article/10.1023/A:1012487302797
- Sklearn的用法:https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.RFE.html#sklearn.feature_selection.RFE
5.3.1 问题描述和此前的工作
1. 分类问题
这篇中我们要解决分类问题,其中输入向量是一个n维向量,包括n个成分(特征)的模式。 F F F为n维特征空间。在此问题中,特征是基因表达系数,模式对应着病人。我们将其限制为一个两分类问题。我们分别用 + + +和 − - −表示两个类。训练数据集中特征分别为 { X 1 , X 2 , . . . , X k , . . . , X l } \{X_1, X_2, ..., X_k, ..., X_l\} {X1,X2,...,Xk,...,Xl},标签分别为 { y 1 , y 2 , . . . , y k , . . . , y l } \{y_1, y_2, ..., y_k, ..., y_l\} {y1,y2,...,yk,...,yl}, y k ∈ { − 1 , + 1 } y_k \in \{-1, +1\} yk∈{−1,+1}。训练模式被用于构建一个决策函数(或者是判别函数) D ( X ) D(X) D(X),其是输入模式 X X X的一个标量函数。新的模式能够根据决策函数的符号来分类:
{ D ( X ) > 0 ⇒ x ∈ c l a s s ( + ) D ( X ) < 0 ⇒ x ∈ c l a s s ( − ) D ( X ) = 0 , d e c i s i o n b o u n d e r y . \begin{cases} D(X) > 0 \Rightarrow x \in class(+) \\ D(X) < 0 \Rightarrow x \in class(-) \\ D(X) = 0, decision\ boundery. \end{cases} ⎩⎪⎨⎪⎧D(X)>0⇒x∈class(+)D(X)<0⇒x∈class(−)D(X)=0,decision boundery.
如果决策函数是训练模式的简单加权和加上偏置量,则称之为线性判别函数( linear discriminant functions)。可通过符号表示为:
D ( X ) = W ⋅ X + b D(X) = W \cdot X + b D(X)=W⋅X+b
其中 W W W是权重向量,b是偏移量。
如果线性判别函数可以将数据集完全分开(没有错误),那么该数据集是线性可分的(“linear separable")。
2. 空间特征降维与特征选择
一个常见的问题是分类是特异性的,而机器学习是普遍性的,找到方式来降低特征空间 F F F的维度 n n n,能够降低**过拟合(“overfitting”)的风险。当特征数目 n n n非常大(我们的案例里中成千上万个基因)并且训练模式 n n n相对较小(几十个病人)**时,数据过拟合很容易出现。 在这种情形下,很容易找到一个简单的决策函数来区分训练集的数据(甚至是线性决策函数),但是在测试数据集上表现非常差。使用正则化的训练技术能够在某种程度上避免数据的过拟合,而不需要空间维度降低。在此情况下,支持向量机(Support Vector Machines, SVMs) 。但是,我们也会在实验结果部分展示,即便是支撑向量机也会受益于空间维度降低。
数据在一些主要方向上的投影是一种常用的降低特征空间维度的方法。使用这种方法,新的特征可以通过原始特征的线性组合来获取。投影方式的一个缺点是原始的特征都不能够丢弃。在这篇文章中,我们研究剪除技术,消除一些原始的输入特征和保留一个最小的特征子集,产生最佳的分类性能。修剪技术是我们感兴趣的应用。为了建立诊断测试,能够选择一小部分基因是非常重要的。原因包括成本效益和易于验证所选基因的相关性。
特征选择问题在机器学习中是众所周知的。关于特征选择的回顾,见例(Kohavi R, John G H. Wrappers for feature subset selection[J]. Artificial intelligence, 1997, 97(1-2): 273-324.)。给定一种特定的分类技术,可以通过对所有特征子集的**穷举(exhaustive enumeration)**来选择满足给定“模型选择”标准的最佳特征子集。关于模型选择的回顾,见例(Kearns M, Mansour Y, Ng A Y, et al. An experimental and theoretical comparison of model selection methods[J]. Machine Learning, 1997, 27(1): 7-50.)。由于子集数量的组合爆炸,对于大量特征(在我们的例子中是数千个基因)来说,穷举枚举是不切实际的。在讨论部分(第六节),我们将回到这种方法,它可以与另一种方法结合使用,这种方法首先将特征的数量减少到一个可管理的大小。
因此,在大维度输入空间中执行特征选择涉及贪婪算法。在各种可能的方法中,特征排序技术尤其具有吸引力。为进一步分析或设计分类器,可以选择固定数量的排名最高的特征。也可以根据排序标准设置阈值。仅保留条件超过阈值的特性。在结构风险最小化(see e.g. Vapnik, 1998 and Guyon, 1992)的原则下,可以使用排名定义嵌套的特征子集 F 1 ⊂ F 2 ⊂ … ⊂ F F_1⊂F_2⊂…⊂F F1⊂F2⊂…⊂F,并选择一个最优的特征子集模型选择准则通过改变一个参数:特征的数量。下面,我们将比较几种特征排序算法。
3. 使用相关系数的特征排序
在下面研究的测试问题中,不可能通过单个基因实现无错误的划分。当增加基因数量时,可获得较好的结果。经典的基因选择方法选择对训练数据进行最佳分类的基因。这些方法包括相关法和表达比例法。它们消除了对辨别无用的基因(噪音),但它们不会产生紧凑的基因集,因为基因是冗余的。此外,个别不能很好地分离数据的互补基因也被遗漏了。
评估单个特征对分离(例如癌症vs.正常)的贡献可以产生一个简单的特征(基因)排序。各种相关系数被用作排名标准。(Golub, 1999)中使用的系数定义为:
w i = ( μ i ( + ) − μ i ( − ) ) / ( σ i ( + ) + σ i ( − ) ) wi = (μ_i(+) - μ_i(-)) / (σ_i(+)+ σ_i(-)) wi=(μi(+)−μi(−))/(σi(+)+σi(−))
其中, μ i μ_i μi和 σ i σ_i σi是所有(+)或(-)类患者中基因 i i i表达值的平均值和标准差, i = 1 , … n i=1,…n i=1,…n。 w i w_i wi正值越大,表示与 c l a s s ( + ) class(+) class(+)相关性越强; w i w_i wi负值越大,表示与 c l a s s ( − ) class(-) class(−)相关性越强。(Golub, 1999)最初的方法是选择相等数量的正相关系数和负相关系数的基因。其他人(Furey, 2000)已经使用 w i w_i wi的绝对值作为排名标准。最近,在(Pavlidis, 2000)中,作者使用了相关系数 ( µ i ( + ) − µ i ( − ) ) 2 / ( σ i ( + ) 2 + σ i ( − ) 2 ) (µ_i(+) -µ_i(-))^2 / (σ_i(+)^2 + σ_i(-)^2) (µi(+)−µi(−))2/(σi(+)2+σi(−)2),这与Fisher判别准则(Duda, 1973)相似。
使用相关性方法进行特征排序的特点是所做的隐式正交性假设。每个系数 w i w_i wi是根据单个特征(基因)的信息计算的,不考虑特征之间的相互信息。在下一节中,我们将更加详细地解释这种正交性假设的含义。
4. 排序标准与分类
特征排序的一个可能用途是基于预先选择的特征子集设计类预测器(或分类器)。每个与感兴趣的特征划分相关(或反相关)的特性本身就是这样一个类预测器,尽管它并不完美。基于这种思想,可以使用一种基于加权投票的简单分类方法: 特征按其相关系数进行投票。这就是在(Golub, 1999)中使用的方法。加权投票方案产生一个特定的线性判别分类器:
D ( X ) = W ⋅ ( X − μ ) D(X) = W \cdot (X-\mu) D(X)=W⋅(X−μ)
其中 W W W通过上述式子 w i = ( μ i ( + ) − μ i ( − ) ) / ( σ i ( + ) + σ i ( − ) ) wi = (μ_i(+) - μ_i(-)) / (σ_i(+)+ σ_i(-)) wi=(μi(+)−μi(−))/(σi(+)+σi(−))来定义, μ = ( μ ( + ) + μ ( − ) ) / 2 \mu = (\mu(+)+\mu(-))/2 μ=(μ(+)+μ(−))/2
很有趣的是,将这种分类器与费舍尔线性判别(Fisher’s linear discriminant)关联。此种分类器可以通过上式变换为:
W = S − 1 ( μ ( + ) − μ ( − ) ) W = S^{-1}(\mu(+)-\mu(-)) W=S−1(μ(+)−μ(−))
其中 S S S是 ( n , n ) (n,n) (n,n)的类散射矩阵,定义为:
S = ∑ x ∈ X ( + ) ( X − μ ( + ) ) ( X − μ ( + ) ) T + ∑ x ∈ X ( − ) ( X − μ ( − ) ) ( X − μ ( − ) ) T S = \sum_{x \in X(+)}(X-\mu(+))(X-\mu(+))^T + \sum_{x \in X(-)}(X-\mu(-))(X-\mu(-))^T S=x∈X(+)∑(X−μ(+))(X−μ(+))T+x∈X(−)∑(X−μ(−))(X−μ(−))T
其中 μ \mu μ是整个训练模式上的平均向量。我们定义 X ( + ) X(+) X(+)和 X ( − ) X(-) X(−)分别为 ( + ) (+) (+)和 ( − ) (-) (−)类的训练集。费舍尔线性判别分析的特定形式意味着 S S S是可逆的。如果特征数目 n n n大于例子的数目 l l l, 因为 S S S的秩最多是 l l l, 此时 S S S就不是可逆的。(1999年Golub)的分类器和费舍尔的分类器在形式上特别相似的,因为散射矩阵可以通过对角线元素近似。当所有训练模式中由一个特征值构成的向量在减去类均值后是正交的时,这种近似是精确的。如果特征不相关,即去除类均值后,两个不同特征乘积的期望值为零,则保留一定的有效性。用它的对角元素逼近S是正则化它(使它可逆)的一种方法。但是,在实践中,特征通常是相关的,因此对角线近似是无效的。
我们刚刚建立了特征排序系数可以用作分类器的权值。反过来,权重乘以给定分类器的输入可以用作特征排序系数。以最大值加权的输入对分类决策的影响最大。因此,如果分类器表现良好,那些权重最大的输入对应的是信息量最大的特征。这个方案是前一个方案的推广(问题:这个方案是什么?前一个方案又是什么?)。特别是,有很多算法来训练线性判别函数,可能提供比相关系数更好的特征排序。这些算法包括刚才提到的Fisher线性判别法,以及本文所要讨论的支持向量机。这两种方法在统计学上都被称为“多元”分类器,这意味着它们在训练期间被优化以同时处理多个变量(或特征)。相比之下,(Golub, 1999)的方法是多个“单变量”分类器的组合。
5. 根据敏感性分析进行特征排序
在这一节中,我们展示了基于线性判别分类器权值大小的排序特征是一种有原则的方法。一些作者建议,当一个特征被删除时,使用目标函数的变化作为排名标准(Kohavi, 1997)。对于分类问题,理想的目标函数是误差的期望值,即在无限个例子上计算出的错误率。为了训练的目的,这个理想目标被一个仅在训练实例上计算的代价函数 J J J所代替。这样的代价函数通常是理想目标的一个边界或近似值,选择它是出于方便和效率的原因。因此,计算成本函数 D J ( i ) DJ(i) DJ(i)的变化的想法是,删除一个给定的特征,或等效地,使其权重为零。OBD(Optimum Brain Damage)算法(LeCun, 1990)通过将J进行二阶泰勒级数展开来逼近 D J ( i ) DJ(i) DJ(i)。在 J J J最优时,一阶项可以忽略,得到:
D J ( i ) = ( 1 / 2 ) δ 2 J δ w i 2 ( D W i ) 2 DJ(i) = (1/2)\frac{\delta^2J}{\delta w_i^2}(DW_i)^2 DJ(i)=(1/2)δwi2δ2J(DWi)2
权重 D W i = w i DW_i = w_i DWi=wi的变化对应着除去特征 i i i。OBD算法的作者主张使用 D J ( i ) DJ(i) DJ(i)代替权值的大小作为权值修剪的准则。对于线性判别函数,其代价函数 J J J是 w i w_i wi的二次函数,这两个准则是等价的。例如,最小二乘错误分类器( mean-squared-error classifier),其损失函数为 J = ∑ x ∈ X ∣ ∣ W ⋅ X − y ∣ ∣ 2 J=\sum_{x \in X}||W\cdot X-y||^2 J=∑x∈X∣∣W⋅X−y∣∣2, 并且对于线性支持向量机,在约束条件下其最小化为 J = ( 1 / 2 ) ∣ ∣ W ∣ ∣ 2 J=(1/2)||W||^2 J=(1/2)∣∣W∣∣2。这证明了使用 ( W i ) 2 (W_i)^2 (Wi)2作为特征排名标准的合理性。
6. 递归特征消除
一个好的特征排序标准不一定是一个好的特征子集排序标准(基于所有特征训练模型,可以得到各个特征的排序;但是这样直接选择n个top特征,未必就是最好的特征子集)。准则 D J ( i ) DJ(i) DJ(i)或 ( w i ) 2 (wi)2 (wi)2估计一次删除一个特征对目标函数的影响。当一次删除几个特征时,它们就变得不是最优的,而这对于获得一个小的特征子集是必要的。这个问题可以通过使用下面的迭代过程来克服,我们称之为**递归特征消除(Recursive Feature Elimination)**:
1)训练分类器(优化权重 w i w_i wi和对应的损失函数 J J J;
2)计算所有特征的排序标准( D J ( i ) DJ(i) DJ(i)或 ( w i ) 2 (wi)2 (wi)2);
3)通过最小排序标准来删掉特征。
这个迭代流程是**反向特征消除(backward feature elimination)**的一个实例。由于计算的原因,一次删除几个特征可能更有效,但代价是可能的分类性能下降。在这种情况下,该方法生成特征子集排名,而不是特征排名。特征子集是嵌套的 F 1 ⊂ F 2 ⊂ … ⊂ F F_1⊂F_2⊂…⊂F F1⊂F2⊂…⊂F。
如果一次删除一个特征,也会有相应的特征排名。然而,排名靠前(最后被删除)的功能不一定是最相关的。在某种意义上,只有将特征子集 F m Fm Fm综合在一起才是最优的。
应该注意到,递归特征消除(Recursive Feature Elimination)对基于相关的特征选择方法没有影响,因为排名标准是根据单个特征的信息计算的。
5.3.2 使用支持向量机(SVM)的特征排名
1. 支持向量机(SVM)
为了验证使用分类器的权重来产生特征排序的想法,我们使用了一种最先进的分类技术:支持向量机(SVMs, Support Vector Machines) (Boser, 1992;Vapnik, 1998)。最近对支持向量机进行了深入研究,并对各种技术进行了基准测试(例如,参见(Guyon, 1999))。它们是目前最著名的分类技术之一,与它们的竞争者相比,具有计算优势(Cristianini, 1999)。
尽管支持向量机处理任意复杂的非线性决策边界,但由于所研究的数据集的性质,我们在本文中将自己限制在线性支持向量机上。线性支持向量机是一种特殊的线性判别分类器。如果训练数据集是线性可分的,那么线性支持向量机就是一个最大边缘分类器。决策边界(在二维分离的情况下是一条直线)被定位为在每一边留下最大的可能的边界。支持向量机的一个特殊性是,决策函数 D ( x ) D(x) D(x)的权值 W i W_i Wi只是训练样本的一个小子集的函数,称为“支持向量”。这些是最接近决策边界的样本。支持向量的存在是支持向量机计算特性和分类性能竞争的根源。支持向量机的决策函数是建立在边界情况下的支持向量上的,其他方法如Golub等人(Golub, 1999)的方法则是建立在平均情况下的决策函数上的。正如我们将在讨论部分(第六节)中看到的,这也会对特征选择过程产生影响。
在本文中,我们使用了(Cortes, 1995)中描述的软边界算法的一种变体。训练包括执行以下二次程序:
Algorithm SVM-train:
**输入:**训练样本 { X 1 , X 2 , . . . , X k , . . . , X l } \{X_1, X_2, ..., X_k, ..., X_l\} {X1,X2,...,Xk,...,Xl}和分类标签 { y 1 , y 2 , . . . , y k , . . . , y l } \{y_1,y_2,...,y_k,...,y_l\} {y1,y2,...,yk,...,yl}。
{ 最 小 化 α k : J = ( 1 / 2 ) ∑ h k y h y k α h α k ( X h ⋅ X k + λ δ h k ) − ∑ k α k 其 中 , 0 ≤ α k ≤ C 并 且 ∑ k α k y k = 0 \begin{cases} 最小化\alpha_k: \\ \\ J = (1/2)\sum_{hk}y_hy_k\alpha_h\alpha_k(X_h \cdot X_k + \lambda\delta_{hk})-\sum_k \alpha_k \\ \\ 其中,0 \leq \alpha_k \leq C 并且 \sum_k \alpha_k y_k = 0 \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧最小化αk:J=(1/2)∑hkyhykαhαk(Xh⋅Xk+λδhk)−∑kαk其中,0≤αk≤C并且∑kαkyk=0
输出: 参数 α k \alpha_k αk。
所有训练模式 X k X_k Xk的求和都是 n n n维特征向量, x h ⋅ x k x_h \cdot x_k xh⋅xk表示标量积, y k y_k yk将类标签(+1或-1), δ h k \delta_{hk} δhk为Kronecker符号( h = k h=k h=k时 δ h k \delta_{hk} δhk,否则为0),λ和C为正常数(软边距参数)。即使问题是非线性可分或条件不佳时,软边界参数也能保证收敛。在这种情况下,一些支持向量可能不在边际上。大多数作者使用λ或c,我们使用一个小的λ值( 1 0 − 14 10^{-14} 10−14的量级),以确保数值的稳定性。对于正在研究的问题,解决方案对C的值相当不敏感,因为训练数据集是线性可分的,只有几个特征。C=100是足够的。
输入向量 X X X的决策函数为:
D ( X ) = W ⋅ X + b , 其 中 w = ∑ k α k y k X k 并 且 b = < y k − W ⋅ X k D(X) = W \cdot X +b, 其中w=\sum_k \alpha_k y_k X_k \quad 并且 b = <y_k - W \cdot X_k D(X)=W⋅X+b,其中w=k∑αkykXk并且b=<yk−W⋅Xk
权值向量 W W W是训练模式的线性组合。大多数权值 α k \alpha_k αk是零。非零权值的训练模式为支持向量。权值满足严格不等式 0 < α k < C 0 \lt α_k \lt C 0<αk<C的为边际支持向量。偏置值b是边际支持向量的平均值。
支持向量机有很多资源,包括其计算机实现:http://www.kernel-machines.org/
2. SVM迭代特征消除(SVM RFE)
支持向量机RFE是利用权重大小作为排序标准的RFE的一种应用。
我们在下面概述了线性情况下的算法,使用Algorithm SVM-train式(5)中的SVM训练。在讨论部分(第六节)提出了非线性情况的扩展。
Algorithm SVM-RFE:
输入:训练样本 X 0 = [ X 1 , X 2 , . . . , X k , . . . , X l ] T X_0=[X_1, X_2, ..., X_k,...,X_l]^T X0=[X1,X2,...,Xk,...,Xl]T, 分类标签 y = [ y 1 , y 2 , . . . , y k , . . . , y l ] y=[y_1, y_2, ..., y_k, ..., y_l] y=[y1,y2,...,yk,...,yl]。
初始化:
幸存特征子集 S = [ 1 , 2 , . . . , n ] S=[1,2,...,n] S=[1,2,...,n]
特征排序列表 r = [ ] r = [\quad] r=[]
重复直到终止 S = [ ] S=[\quad] S=[]
限制训练样本来获得好的特征划分: X = X 0 ( : , S ) X=X_0(:,S) X=X0(:,S)
训练分类器: α = S V M − t r a i n ( X , y ) \alpha = SVM-train(X,y) α=SVM−train(X,y)
计算维度长度 ( S ) (S) (S)的权重向量: w = ∑ k α k y k X k w = \sum_k \alpha_ky_kX_k w=∑kαkykXk
计算排序标准: c i = ( W i ) 2 , 对 所 有 的 i c_i = (W_i)^2,对所有的i ci=(Wi)2,对所有的i
使用最小排序标准来寻找特征: f = a r g m i n ( C ) f=argmin(C) f=argmin(C)
更新特征列表: r = [ S ( f ) , r ] r=[S(f), r] r=[S(f),r]
根据最小排序标准来清除特征: S = S ( 1 : f − 1 , f + 1 : l e n g t h ( S ) ) S=S(1:f-1, f+1:length(S)) S=S(1:f−1,f+1:length(S))
输出:特征排序列表 r r r。
如前所述,由于速度的原因,该算法可以一般化,每步删除一个以上的特征。
5.3.3 基于sklearn的递归特征消除
参考:https://scikit-learn.org/stable/auto_examples/feature_selection/plot_rfe_digits.html#sphx-glr-auto-examples-feature-selection-plot-rfe-digits-py
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.feature_selection import RFE
import matplotlib.pyplot as plt# Load the digits dataset
digits = load_digits()
X = digits.images.reshape((len(digits.images), -1))
y = digits.target# Create the RFE object and rank each pixel
svc = SVC(kernel="linear", C=1)
rfe = RFE(estimator=svc, n_features_to_select=1, step=1)
rfe.fit(X, y)
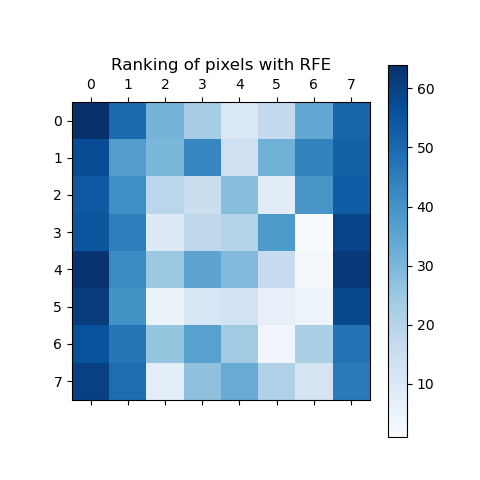
ranking = rfe.ranking_.reshape(digits.images[0].shape)# Plot pixel ranking
plt.matshow(ranking, cmap=plt.cm.Blues)
plt.colorbar()
plt.title("Ranking of pixels with RFE")
plt.show()
结果为:
5.3.4 REF与交叉验证的关系
参考:https://scikit-learn.org/stable/auto_examples/feature_selection/plot_rfe_with_cross_validation.html
一个特征消除的例子,通过交叉验证自动调整选择的特征数目:
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.model_selection import StratifiedKFold
from sklearn.feature_selection import RFECV
from sklearn.datasets import make_classification# Build a classification task using 3 informative features
X, y = make_classification(n_samples=1000,n_features=25,n_informative=3,n_redundant=2,n_repeated=0,n_classes=8,n_clusters_per_class=1,random_state=0,
)# Create the RFE object and compute a cross-validated score.
svc = SVC(kernel="linear")
# The "accuracy" scoring shows the proportion of correct classificationsmin_features_to_select = 1 # Minimum number of features to consider
rfecv = RFECV(estimator=svc,step=1,cv=StratifiedKFold(2),scoring="accuracy",min_features_to_select=min_features_to_select,
)
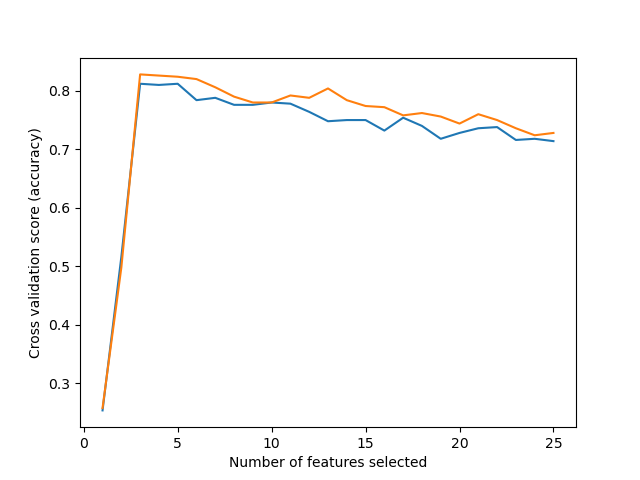
rfecv.fit(X, y)print("Optimal number of features : %d" % rfecv.n_features_)# Plot number of features VS. cross-validation scores
plt.figure()
plt.xlabel("Number of features selected")
plt.ylabel("Cross validation score (accuracy)")
plt.plot(range(min_features_to_select, len(rfecv.grid_scores_) + min_features_to_select),rfecv.grid_scores_,
)
plt.show()
结果为:
输出为:
/home/circleci/project/sklearn/utils/deprecation.py:103: FutureWarning: The `grid_scores_` attribute is deprecated in version 1.0 in favor of `cv_results_` and will be removed in version 1.2.
warnings.warn(msg, category=FutureWarning)
这篇关于递归特征消除(Recursive Feature Elimination)原理与Sklearn实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





