层次分析法（The analytic hierarchy process, 简称AHP）

层次分析法

(The analytic hierarchy process, 简称AHP)建模比赛中最基础的模型之一，其主要用于解决评价类问题（例如：选择哪种方案最好、哪位运动员或者员工表现的更优秀）。

评价类问题，首先考虑几个问题：

• 1、评价的目标。
• 2、为了达到这个目标有哪几种可选的方案。
• 3、评价的准则/指标。（根据题目的背景材料、常识及网上的参考资料）

•  知网：https://www.cnki.net/ 			百度学术：https://xueshu.baidu.com/万方数据：http://www.wanfangdata.com.cn/index.html
  

如何使用层次分析法？

首先，我们要做的就是填满这个表，那么这些数据怎么来呢？

• 确定指标的判断矩阵（计算指标权重一列）：

一次性考虑所有指标之间的关系，往往考虑不周。所以将两个两个指标进行比较，最终根据两两比较的结果来推算出权重。


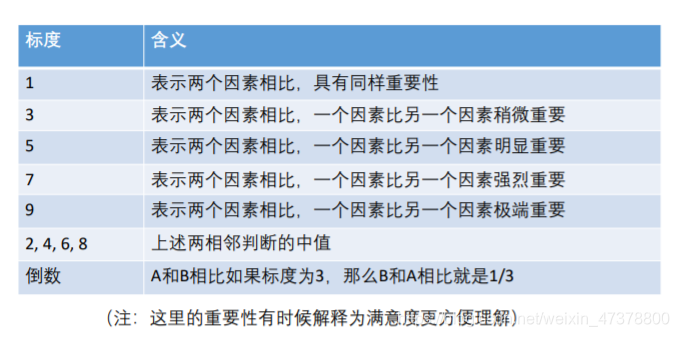
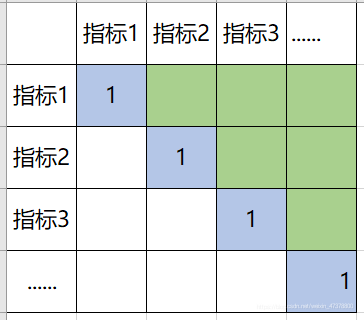
总结：上面这个表是一个n×n（n个指标）的方阵，我们记为A，对应的元素为aij.
这个方阵有如下特点：
（1）aij表示的意义是，与指标𝑗相比，𝑖的重要程度。
（2）当i=j时，两个指标相同，因此同等重要记为1，这就解释了主对角线元素为1。
（3）aij> 0且满足aij×aji=1 （我们称满足这一条件的矩阵为正互反矩阵）
实际上，上面这个矩阵就是层次分析法中的判断矩阵。

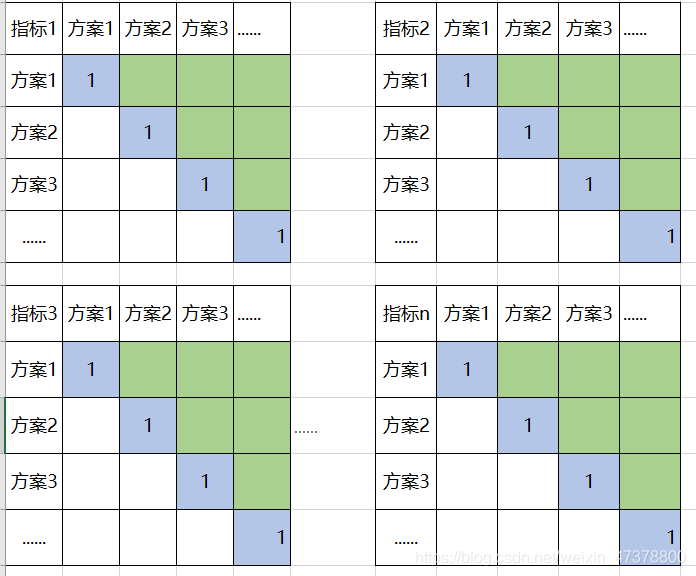
• 确定所有方案在某个指标上的判断矩阵（计算某个方案在某个指标上的权重）
  （有几个指标，就有几个判断矩阵，注意数据是否会出现不一致现象）
  

• 一致性检验&权重的几种计算方式

  若正互反矩阵满足aij×ajk=aik，则我们称其为一致矩阵。
  注意：在使用判断矩阵求权重之前，必须对其进行一致性检验。
  原理：
  

• 一致性检验步骤：
  

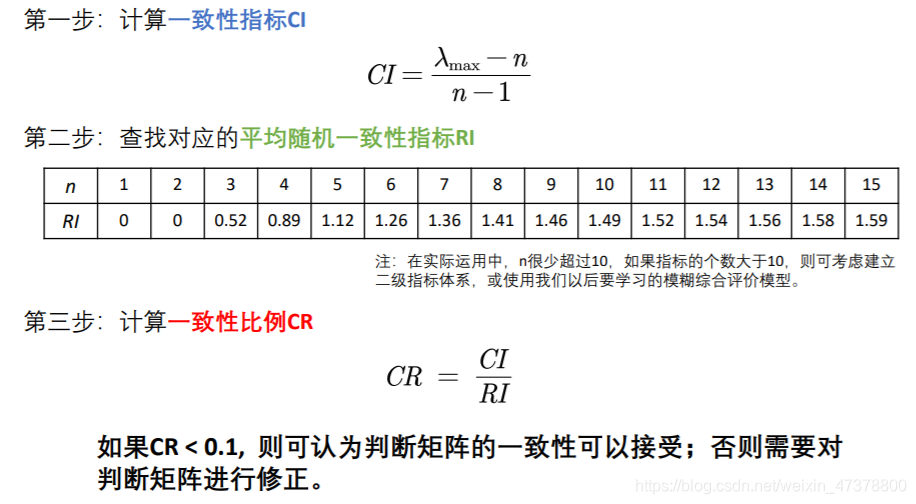
  • 权重计算方法1：算术平均法求权重
    
  • 权重计算方法2：几何平均法求权重
    
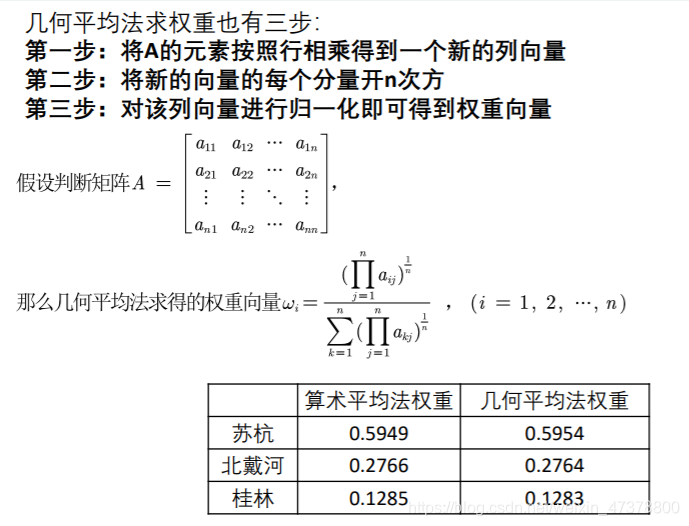
  • 权重计算方法3：特征值法求权重

层次分析在数学建模中的完整步骤

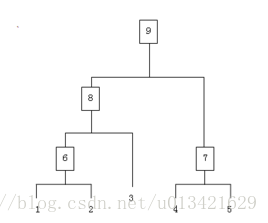
1. 分析系统中各因素之间的关系，建立系统的递阶层次结构
   eg: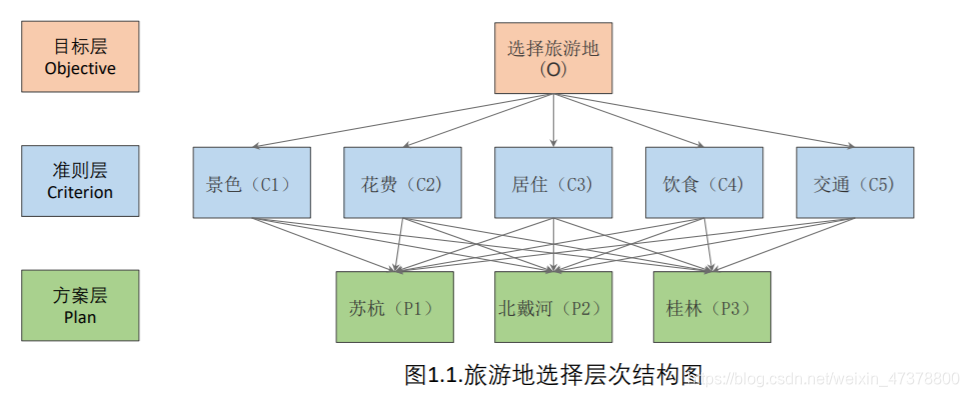

2. 对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，构造两两比较矩阵（判断矩阵）。
   

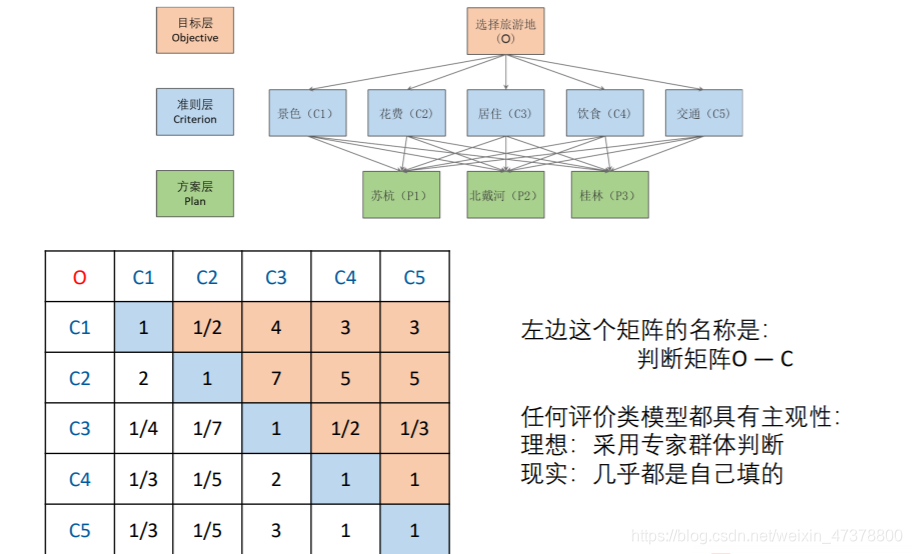
3. 由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验（检验通过权重才能用）
   若要修正，看每行/列的比例进行修正。
   

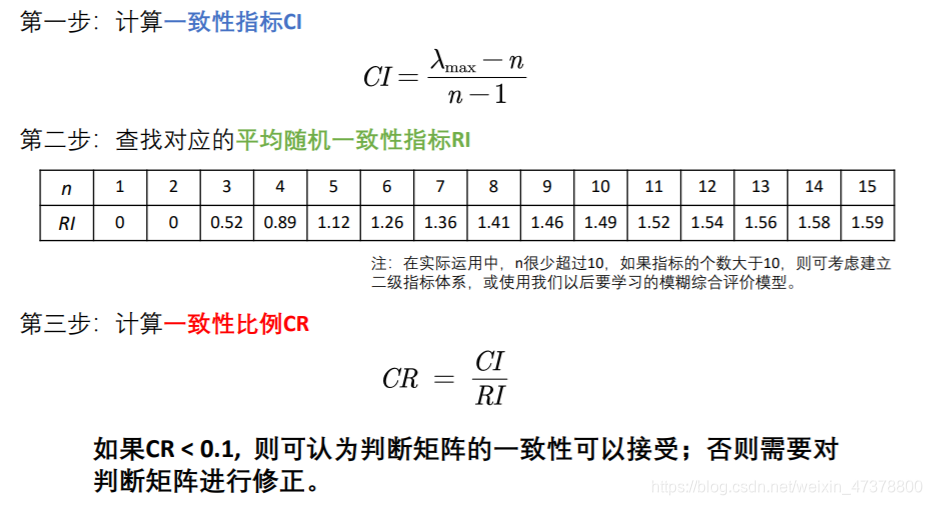
4. 根据权重矩阵计算得分，并进行排序，找到最优选择。