【计量经济学】--经典线性回归

本文主要是介绍【计量经济学】--经典线性回归，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

计量经济学的组成：
经济理论+数学+统计推断；

计量经济学的定义：
实际经济现象的定量分析，利用数理统计分析经济数据，对于构建于数理经济学基础上的数学模型提供经验支持，并得出数量结果；

计量经济的主要作用：
验证经济理论、经济结构分析、经济政策评价、经济预测。

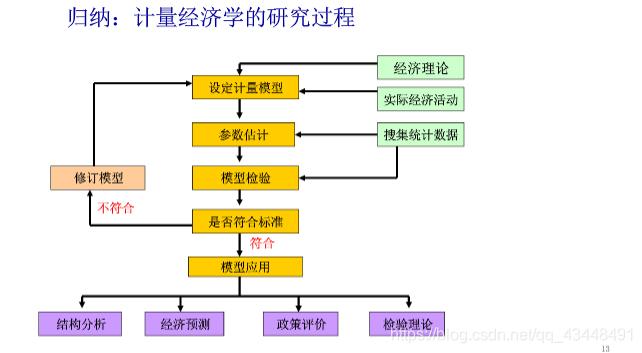
四个步骤：
模型设定（specification)、估计参数、模型检验、模型应用

模型设定
计量模型构成要素：变量、参数和随机扰动项；
估计参数
一般地，参数是未知的，不可直接观测。参数要通过样本数据，选择适当方法加以估计，如普通最小二乘法（OLS)，极大似然法（ML)、广义最小二乘法（GLS)
模型检验
经济意义检验：所估计的模型与经济理论是否相符；
统计推断检验：检验参数估计值是否是抽样的偶然结果；
计量经济学检验：是否符合计量经济方法的基本假定；
预测检验：将模型预测结果与经济运行的实际对比；

在这里插入图片描述

经济变量之间的相互关系的三种情况：
确定性的函数关系，可以使用数学方法计算；
不确定性的统计关系，即相关关系，可以用统计方法分析；
没有关系；

相关分析：
相关关系是指变量间不确定性的依存关系。
总体的两个变量X和Y的全部数值无法直接观测，所以总体相关系数也是未知的，一般考虑使用样本相关系数估计总体相关系数。不过，对于特定的总体，X和Y的数值是既定的，那么总体相关系数 $\rho$ 是客观存在的特定数值。
相关系数存在的弊端：
1. 不能说明一个变量的变动会导致另一个变量变动的具体数量规律。
2. 样本相关系数是总体相关系数的样本估计值，由于抽样波动，样本相关系数是随抽样而变动的随机变量，其统计显著性还有待检验。

回归（regression）分析：
回归分析是研究一个因变量的变量（Y）对另一个或多个叫自变量的变量（X）的依赖关系。
通过自变量在重复抽样中的已知或设定值，去估计或预测因变量的总体均值。
总体回归直线是解释变量取各给定值时，被解释变量条件期望的轨迹。

因变量，被解释变量explained variable；
自变量，解释变量explainatory variable；

条件分布和条件概率
当解释变量X取某固定值时，被解释变量Y值不确定，Y的不同值会形成一定的分布，即Y的条件分布。
X取某固定值时，Y取不同值的概率称为条件概率，从而有Y的条件期望，用 $E(Y|X_{i})$ 表示，该值会随X的变动而变动。
回归线
对于每一个X的取值 $X_{i}$ ，都有Y的条件期望 $E(Y|X_{i})$ 与之对应，那么点 $X_{i}，E(Y|X_{i})）$ 的轨迹形成的曲线或直线就是回归线。
回归函数
$f(X_{i})=E(Y|X_{i})$
样本相关系数 $r$ 和样本可决系数 $r^{2}$ 在概念上的区别：
$r$ 建立在相关分析的理论基础上，研究两个随机变量 $X$ 与 $Y$ 之间的线性相关关系； $r^{2}$ 建立在回归分析的理论基础上，研究非随机变量 $X$ 对随机变量 $Y$ 的解释程度；

关于拟合优度检验

既然最小二乘法所得到的参数估计已经具有较好的统计性质（无偏性、线性性、最小方差性等），还要对得到的样本回归线进行拟合优度检验，计算可决系数呢？
这是因为一些散点图做出来并不呈线性相关的数据，带入最小二乘计算参数的公式中，就能得到所谓的“回归线“，而它是没有实际意义的，。于是为了避免这一现象的产生，提出了拟合优度的概念。