右手坐标系下LookAt视图矩阵的推导

本文主要是介绍右手坐标系下LookAt视图矩阵的推导，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

http://www.cnblogs.com/bluebean/p/5275541.html

右手坐标系下LookAt视图矩阵的推导

基本知识

右手坐标系

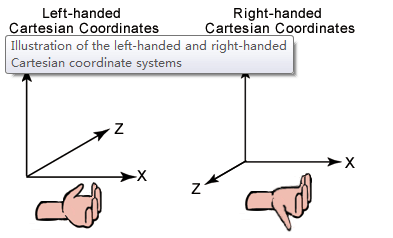
右手手掌弯曲，手指方向由正X轴指向正Y轴，如果这时Z轴正方向与大拇指方向保持一致，坐标系为右手坐标系，否则为左手坐标系。

向量叉乘的方向

向量(1,0,0)与向量(0,1,0)叉乘的结果可以由公式计算得到为(0,0,1),在数值上它是始终不变的。但放在坐标中进行解释，(0,0,1)都是代表Z轴正方向，但在左右手坐标系中他们与X,Y轴正方向的相对空间位置是不同的。在右手坐标中判断叉乘结果的方向使用右手定律，左手坐标系中使用左手。

视图变换是三维渲染中物体顶点坐标变换的一部分，完整的流程为：

1使用Module矩阵将物体顶点坐标从物体坐标系转换至世界坐标系

2使用View矩阵将物体顶点坐标从世界坐标系转换至由摄像机定义的坐标系，摄像机坐标系原点在摄像机，Z轴方向沿着视线方向往前，y轴方向即摄像机的向上向量。

3.使用透视投影矩阵及透视除法将位于视锥体内的顶点坐标转换到X,Y,Z范围都为-1至1.

摄像机特点：

三维自由运动的物体有六个运动自由度，分别是X,Y,Z方向的平移和绕X,Y,Z轴的选择。绕Z轴的旋转使物体发生侧向倾斜，如果站在人的角度考虑的话，就是向左或向右倾斜了，这个自由度在大部分情况是可以不要的，他更容易使人产生眩晕感。所以这里的摄像机拥有剩余的五个自由。绕X轴选择代表了仰视和俯视，绕Y轴旋转代表了旋转自身，比如从向东旋转到向西。

View矩阵的工作原理

View矩阵的工作目标是将世界坐标系中的所有物体的顶点的坐标从世界坐标系转换到摄像机坐标系。

摄像机坐标系的原点不一定与世界坐标系重合，同时由于自身的旋转，坐标轴也一定不与世界坐标系的坐标轴平行。为完成工作任务，需要分为两步走1.整体平移，将摄像机平移至世界坐标系原点，2.将坐标点从世界坐标系转换至摄像机坐标系。

使用单位向量U,V,W分别代表摄像机坐标系X,Y,Z轴正向的单位向量在世界坐标系中的表示，则在摄像相机坐标系与世界坐标系原点重合的情况下，物体顶点坐标代表的向量（即从世界原点指向物体顶点的向量）在U,V,W上的投影大小即是物体顶点在摄像机坐标系下的坐标值。因为U,V,W是单位向量，使用二者的点乘即可以得到顶点的投影大小。

Lookat函数的一般形式

LookAt(Vector3 eyePos,Vector3 targerPos,Vector3 upDir,Matrix4 & ViewMatrix);

函数的参数：eyePos代表了摄像机在世界坐标系中的坐标，targetPos代表了视线方向上某个目标物体的坐标，upDir一般使用的是世界坐标系中的向上向量，即（0,1,0）.

这个函数将传入的最后一个参数设置为前面参数所指定的View矩阵。

首先要先求得摄像机坐标系的U,V,W。

1.首先已知eyePos和tarPos，可以求得视线方向，视线方向由eyePos指向tarPos,所以viewDir=tarPos-eyePos，W=viewDir.normalize()

2.U=crossProduct(upDir,W) U=U.normalize()

upDir一般是向量(0,1,0)，所以求得的U向量必然是平行于地面，而如果物体绕Z轴选择，X轴将不再平行于地面。说明使用upDir为(0,1,0)时计算U,V,W的计算方法默认摄像机只有两个旋转自由度。

3.V=crossProduct(W,U) V.normalize()

注意：这里使用右手坐标系，使用向量叉积计算U,V时，crossProduct()函数的参数的顺序是重要的。叉乘结果向量的方向符合右手法则。

现在View矩阵可以由两个矩阵合成，一个是将摄像机平移至原点的矩阵T，一个是将坐标点从世界坐标系转换至摄像机坐标系的矩阵R。

大概的代码表示的流程

void Matrix4X4::initLookAtMatrix(const Vector3& eyePos, const Vector3& targetPos, const Vector3& updir) 
{Vector3 eye = eyePos;Vector3 tar = targetPos;Vector3 up = updir;Vector3 W = tar - eye;W.normalize();Vector3 U = Vector3::crossProduct(up, W);U.normalize();Vector3 V = Vector3::crossProduct(W, U);V.normalize();float m[4][4] = { { U.x,U.y,U.z,0 },{ V.x,V.y,V.z,0 },{ W.x,W.y,W.z,0 },{ 0,0,0,1 } };Matrix4X4 coordiTransformMatrix(m);Matrix4X4 contraryTranslation;contraryTranslation.initTranslationMatrix(-eyePos.x, -eye.y, -eye.z);*this = coordiTransformMatrix*contraryTranslation;}

个人理解：

ViewMatrix 矩阵分解的旋转矩阵，每一行，都是其相机在世界坐标系的三个朝向分量（上下、前后、左右）平移分量为负，表示是转换为相机坐标系参考原点，原来物体对相机的相对位置即为负向。

这篇关于右手坐标系下LookAt视图矩阵的推导的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！