（四）2.自动控制原理 The Root Locus Method 绘制根轨迹的八条法则

我们上节课了解了根轨迹是什么东西，学到了怎么去判断一个点是不是根轨迹上的点
但怎么去画根轨迹没有提及，这次我们说说绘制根轨迹的法则

法则一：起点终点

根轨迹起点： 开环极点
根轨迹终点： 开环零点
如果极点数n>零点数m  则有n-m个根轨迹指向无穷

说的玄乎，实际上起点就是 k’ = 0的时候，终点就是 k’ = ∞的时候

证明：
前面提过的根轨迹上点的模值条件：|开环传递函数| = 1 = k’ ×（∏ x-开环零点/∏ x-开环极点）

==》k’ = ∏(x - 开环极点)/∏(x - 开环零点) = s^(n-m) * ∏(1 - 开环极点/s)/∏(1 - 开环零点/s)

k’ = 0 ====》 x = 开环极点
k’ = ∞ ====》x = 开环零点 or x = ∞

从而，我们得到，根轨迹的起点都是开环极点，终点是开环零点或者无穷远处

法则二：根轨迹分支数，对称性和连续性

根轨迹分支数 = 开环极点数/特征方程的阶数
根轨迹连续
根轨迹对称于实轴

法则三，实轴上的根轨迹

这个点的右边的极点或零点个数 为 基数，则这个点是根轨迹上的点
由此得到，从最右向左，每个奇数点和偶数点之间的那一段为根轨迹。否则不是
（极点零点都看成点，不区别对待）

证明：

对于这样一个一般情况的图，我们去分析
思路：在某一段线上取一个点，通过前面的方法去判断这个点在不在根轨迹上来看这个线段是不是根轨迹

证：就像图中画得那样，我们可以看到零点极点如果不是在实轴上，那必然是一堆共轭复根，对于共轭复根，我们根据相角原理，s-p，s-z，发现，每一对共额府根的相角和为360度，这个就告诉了我们，共轭复根对于在实轴上的点的判断是没有影响的，关键还是在于看实轴上的点对于该点的影响。

假设我们取一个点，其右边一共有极点零点 x个，左边的点若干
由于左边的点指向我们待测点相角为0，显然也是不影响的
右边的每个点到待测点相角为180度，x个点，如果x是奇数，那一定是（2k+1）pai，表明成立，否则不成立，如图所示，画出红线的部分显然就是根轨迹的部分

法则四：根之和

在  n - m >= 2 的时候，闭环函数所有的根的和为常数

证明思路： 由代数定理
对于(s-a1)(s-a2)(s-a3)…(s-an) = sⁿ +x n-1 s^n-1 +…+x0
a1+a2+…+an = - x n-1 （n-1是下标）这里我们不多说这个定理，不相信的同学代值算算就能看出点门道来，数学归纳法也许可以证？

下面对这个法则进行证明：
首先 对于开环传递函数，其特征式为开环的分母，
利用上面的定理，得到开环的极点之和为常数 a(n-1) 。a(n-1是给定值)
矛头指向闭环传递函数，他的特征式为开环传递函数的分子加上分母.
由于限制条件n-m<=2，发现分子加分母之后的特征式没有对第二项a(n-1) s^n-1造成影响
由此继续利用上述公式推出，闭环函数所有的根之和为 常数 a(n-1)。

由此法则我们可以知道，当闭环函数的某个根变化时，必然会有与之对应的另外一个根变化，使他们的和不变

5.渐近线

有法则1我们得到，存在终点是无穷的根轨迹，那这个法则就对这n-m条根轨迹给出规律

渐近线和实轴交点σ： (极点之和 - 零点之和)/n-m
渐近线和实轴正方向夹角： (2k+1)π/n-m

证明： 首先 -k’= ∏(s-p)/ ∏(s-z) (极点/零点) = (s-σ)^n-m (因为假设根轨迹上点很远，所以这里吧所有的点都看作σ点) = s^n-m+ (n-m)σ s^n-m-1
前面提过，所有的点的和等于第二项系数的负。所以我们把-k’化简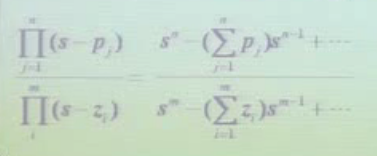
然后利用长出除法：

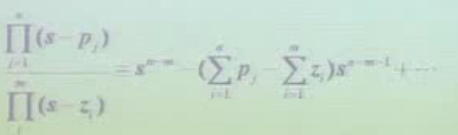
对照我们上面得到的另外一个式子，令第二项相等，得到σ的表达式：
σ(n-m)=(∑p)-(∑z) (极点和-零点和) ，得到第一个公式

下面说角度公式：
同理将所有点看成在一个位置：(2k+1)π = ∑角(s-z)-∑角(s-z) = nψ -mψ = (n-m)ψ
就此第二个公式得到

这个法则用在确定n-m条通往无穷的线，计算出交点和角度，就能确定这条线的渐近线

根据渐进线确定根轨迹方程也有需要注意的点

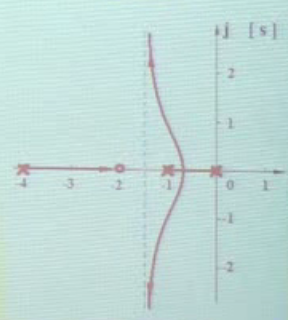
例如这个，渐近线已确定，就是那条虚线：

1.0和-1之间的会和点应该怎么定性确定？-4 ----》-2  向右，如果-1和0在-0.5相遇，就会抵消，显然根据根之和我们不能答应所以我们选择相遇点偏左，这样相遇时还能有个差向左，不影响-4 =》-2
2.画图：根据根之和确定大致形状不越过渐近线（因为-4=》-2不能越过-2）不画出波浪形（因为-1=》-2不能来回波动）老老实实画一个平滑的单调曲线

例如这里问当我们两个点实部是-1的时候，右边的点在哪里？
答：
方法一：-3 我们根据距离渐近线的距离来计算 显然还有0.5×2 到达目标，那-4=》-2 也还差1，就是-3
方法二：看开环函数的极点，相加取反之后应该等与 -5，现在我们是-1-1 = -2，还差 -3，所以答案 -3

6.分离点

我们刚才定性的确定了分离点靠近哪边，但是显然达不到要求，现在我们看看分离点的算法

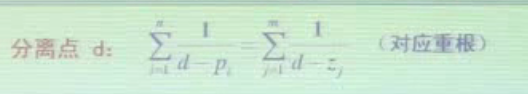
无零点时右边为0！！！

解出d就是分离点，这里不证明了，记一下吧（我没证过但我觉得满足根之和应该是一个列方程的办法（滑稽））
一般不是那么容易解出来，我们可以试根，上面知道了定性判断的方法，确定了区间试出来应该不是特别麻烦，一般近似

7.求根轨迹和虚轴交点

遇到那种渐近线偏着，导致根轨迹会和虚轴相交的情况，求出交点更能帮助画轨迹线

方法一：根轨迹和虚轴交点，实际上就是临界稳定点所以得到解法：1.写闭环函数，得到特征式2.画出劳斯表3.劳斯表第一列出现全零行，求出K'	4.用上面一行写出辅助方程，得到的根就是交点了
方法二:向特征式中用（jw）代替 S，分离出实部虚部都 = 0解出w 和K' 的值，就是交点

给个例题结合法则567

8.出射角入射角

就是我们前面常说的相角条件
给个例题，这儿不说了，就是一个算根轨迹曲线的刚开始的入射角度和到达时候的出射角度来确定曲线

下面介绍一个定理：

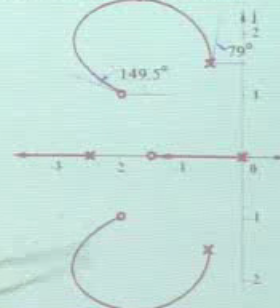
系统两个开环极点，一个开环零点，并且在复平面存在根轨迹
那复平面的根轨迹一定是以零点为圆心的圆

以开环函数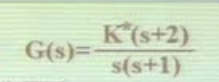为例来说这个定理

证明：这个开环传递函数满足条件，极点 0，-1，零点 -2
写出他的特征式子即根轨迹方程 ：k’(S+2)+S(S+1) = S² +( 1+k’)S +2k’ = 0;
我们可以写出他的两个根：

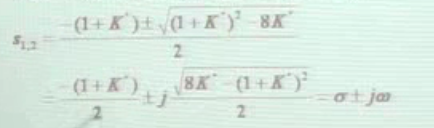
那我们下面要做的事情很显然，我们的目的是求出轨迹曲线方程，现在极点的横纵坐标都可以用K’表示，那我们显然可以写出曲线方程了

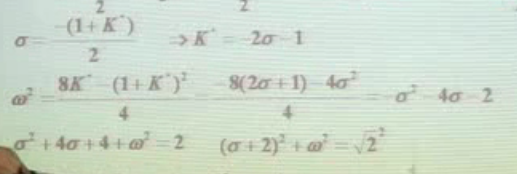
至此我们成功证明了定理，所用例题的轨迹图如下
通过这个图我们可以分析一下系统动态性能指标

1.从极点出发到实轴的分离点：因为两个极点在实轴上，所以过阻尼系统，超调量为0，因为主极点远离虚轴，所以调节时间变小
2.圆环部分：得到是欠阻尼系统，从前面学习二阶性能的时候得到的公式：1.超调量先变大（相切）再变小     cos beta = 超调量2.两个根离开虚轴，调节时间变小
3.到了实轴，又变成过阻尼的状态了：过阻尼系统，超调量为0，又因为主极点靠近了零点，所以抵消，调节时间变小

系统是否稳定的判断

根轨迹在虚轴左边所以稳定从前面静态误差系数法得到，K'变大，稳态误差A/.. 所以变小

下面给出不同位置的点的根轨迹的表格：
再给个例题吧

画根轨迹的题目并不是每个方法都要用，完全随心，就是所谓的无招胜有招吧
但是为了大家能拿到题目不会一头雾水，我们还是给几个建议

1.找到所有的零极点
2.确定实轴上的轨迹
3.如果极点比零点多的话，确定渐近线
4.如果渐近线是偏着向虚轴的话，计算与虚轴交点和入射出射角如果渐近线垂直，那应该就不需要，有共轭点的话最好算一下角度

画根轨迹很重要啊，多练一练吧，等到真正工程实践，这八个法则完全是模糊的，但是我们已经有感觉了，看到零极点分布就可以条件反射，按照感觉给出根轨迹图