《Detecting sequences of system states in temporal networks》

论文地址

https://www.nature.com/articles/s41598-018-37534-2

bibtex

@article{DBLP:journals/corr/abs-1803-04755,author    = {Naoki Masuda andPetter Holme},title     = {Detecting sequences of system states in temporal networks},journal   = {CoRR},volume    = {abs/1803.04755},year      = {2018},url       = {http://arxiv.org/abs/1803.04755},archivePrefix = {arXiv},eprint    = {1803.04755},timestamp = {Mon, 13 Aug 2018 16:46:49 +0200},biburl    = {https://dblp.org/rec/journals/corr/abs-1803-04755.bib},bibsource = {dblp computer science bibliography, https://dblp.org}
}

代码地址

https://github.com/naokimas/state_dynamics

主要内容

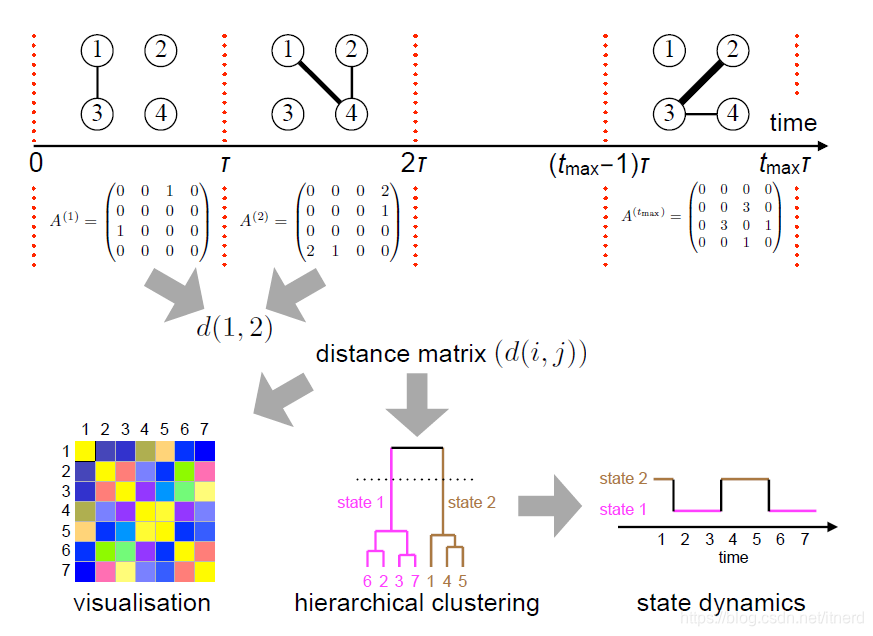
动态网络是由网络快照（snapshot）的序列来描述，这篇文章主要考虑网络的链路是动态变化的，比如通讯网络中，节点之间的通讯状态是时断时续的。

假设一个快照的持续时间为$T$，在这段时间内存在通讯的节点对之间具有连边，用网络的邻接矩阵表示。动态网络序列由网络快照的邻接矩阵组成。

接下来要识别这些邻接矩阵的状态，核心思想就是（层次）聚类。

聚类算法的核心是求元素之间的距离，即网络邻接矩阵间的距离。

网络的距离度量

图编辑距离

$$d=N(G_1)+N(G_2)-2N(G_1\cap G_2)+M(G_1)+M(G_2)-2M(G_1\cap G_2)$$其中，$N(\cdot ),M(\cdot )$ 分别代表节点数和边数。

DeltaCon

@article{10.1145/2824443,
author = {Koutra, Danai and Shah, Neil and Vogelstein, Joshua T. and Gallagher, Brian and Faloutsos, Christos},
title = {DeltaCon: Principled Massive-Graph Similarity Function with Attribution},
year = {2016},
issue_date = {February 2016},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {10},
number = {3},
issn = {1556-4681},
url = {https://doi.org/10.1145/2824443},
doi = {10.1145/2824443},
journal = {ACM Trans. Knowl. Discov. Data},
month = feb,
articleno = {28},
numpages = {43},
keywords = {node attribution, anomaly detection, graph classification, culprit nodes and edges, Graph similarity, network monitoring, graph comparison, edge attribution}
}

The quantum spectral Jensen-Shannon divergence

JS 散度解决了 KL 散度不对称的问题：

KL散度：
$$KL(P||Q)=\sum _{x}P(x)\log \frac{P(x)}{Q(x)}$$
KL散度具有正定性和非对称性。

JS 散度：
$$\begin{gathered} JS(P||Q)=\frac{1}{2}KL(P||M)+\frac{1}{2}KL(Q||M), \\ M=\frac{1}{2}(Q+P) \end{gathered}$$
熵的定义为：
$$H(P)=-\sum _{x}P(x)\log P(x),$$
从熵的角度来看JS散度：$$\begin{array}{rl}JS(P||Q)=& \frac{1}{2}KL(P||M)+\frac{1}{2}KL(Q||M)\\ & \\ =& \frac{1}{2}\left({\sum }_{x}P(x)\log P(x)-{\sum }_{x}P(x)\log M(x)+{\sum }_{x}Q(x)\log Q(x)-{\sum }_{x}Q(x)\log M(x)\right)\\ & \\ =& H(M)-\frac{1}{2}\left(H(P)+H(Q)\right)\end{array}$$
JS散度具有:

1. 正定性且值域为$[0,1]$；
2. 对称性。

JS散度是比较两个分部的距离，怎样用来计算两个网络的相似度呢？

首先定义密度矩阵：
$$\rho =e^{-\beta L}/\sum _{i=1}^N{e}^{-\beta {\lambda }_i}$$
其中，$L=D-A$，$e^{-\beta L}=I-\beta L+\frac{1}{2!}{\beta }^2{L}^2-\frac{1}{3!}{\beta }^3{L}^3+\cdots$， 怎么理解这个式子呢？

其实，$e^{-tL}$ 是网络扩散过程：
$$\dot{x}=-Lx=(A-D)x$$的基本解矩阵，该方程的通解为：$x=e^{-tL}{x}_0$， 而 $\beta$ 控制了网络中扩散的时间。
所以$\rho$可以反映网络中的扩散过程，因而可以作为网络的特征表示。另一方面，$\rho$的特征值之和相加为1，所以$\rho$可以视为量子力学中的密度矩阵（？暂时不懂）。

对于密度矩阵定义冯纽曼熵（von Neumann entropy）：
$$S(\rho )=-\sum _{i=1}^N{\tilde{\lambda }}_i{\log }_2{\tilde{\lambda }}_i,$$其中，${\tilde{\lambda }}_i$是$\rho$的第$i$个特征值.

根据熵和JS散度的关系，得到两个密度矩阵之间的距离度量：
$$d=\sqrt{S(\frac{{\rho }_1+{\rho }_2}{2})-\frac{1}{2}[S({\rho }_1)+S({\rho }_2)]}$$

其余四种频域距离

对于两种拉普拉斯矩阵：
$$\begin{gathered} L=D-A, \\ {L}^{\prime }=I-D^{-1/2}A{D}^{-1/2} \end{gathered}$$
分别取如下两种频域距离度量：
$$d_1=\sqrt{\sum _i^n({\lambda }_i(G_1)-{\lambda }_i(G_2){)}^2}$$ d 2 = ∑ i n ( λ i ( G 1 ) − λ i ( G 2 ) ) 2 max ⁡ { ∑ i n λ i ( G 1 ) 2 , ∑ i n λ i ( G 2 ) 2 } d_2 = \sqrt{\frac{\sum_i^n(\lambda_i(G_1) - \lambda_i(G_2))^2}{\max\{\sum_i^n\lambda_i(G_1)^2 , \sum_i^n\lambda_i(G_2)^2 \}}} d2​=max{∑in​λi​(G1​)2,∑in​λi​(G2​)2}∑in​(λi​(G1​)−λi​(G2​))2​ ​
其中${\lambda }_i$表示第$i$大的特征值.