16 - nn.Conv2d的原理以及三路分支残差block的算子融合实现

本文主要是介绍16 - nn.Conv2d的原理以及三路分支残差block的算子融合实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. R-drop

• 论文链接：R-Drop: Regularized Dropout for Neural Networks

1.1 R-drop 原理

• 算法：
  
• 损失函数：
  
• 贡献
  

2. 常见函数

2.1 torch常见API

• torch.functional.pad
  

import torch
from torch.nn import functional as Fa = torch.ones(2, 3, 4, 5)
paddings_1 = (1, 2, 3, 4, 5, 6, 7, 8)
paddings_2 = (10, 9, 8, 7, 6, 5, 4, 3)
b = F.pad(a, paddings_1)
c = F.pad(a,paddings_2)
print(f"a.shape={a.shape}")
print(f"b.shape={b.shape}")
print(f"c.shape={c.shape}")

a.shape=torch.Size([2, 3, 4, 5])
b.shape=torch.Size([17, 14, 11, 8])
c.shape=torch.Size([9, 14, 19, 24])

• torch.nn.Conv2d (padding=“same”)
  以前我们设置二维卷积的时候需要手动设置padding 的值，特别的麻烦，现在方便了，直接设置padding=“same”，那么可以保证，输入张量经过卷积运算后，输出矩阵的高宽前后保持一致；

import torch
from torch import nnmy_conv2d = nn.Conv2d(in_channels=3,out_channels=5,kernel_size=3,padding="same")
my_input = torch.rand(2,3,10,20)
my_output = my_conv2d(my_input)
print(f"my_conv2d={my_conv2d}")
print(f"my_input.shape={my_input.shape}")
print(f"my_output.shape={my_output.shape}")

my_conv2d=Conv2d(3, 5, kernel_size=(3, 3), stride=(1, 1), padding=same)
my_input.shape=torch.Size([2, 3, 10, 20])
my_output.shape=torch.Size([2, 5, 10, 20])

• torch.isclose()

torch.isclose(input, other, rtol=1e-05, atol=1e-08, equal_nan=False) → Tensor

返回一个新的张量，其布尔元素表示输入的每个元素是否“接近”other的相应元素。亲密度定义为:

如果张量a和张量b中的数据的差值在一定的范围内，那么就返回True，否则返回False

print(torch.isclose(torch.Tensor([1.,2.,3.]),torch.Tensor([1.+1e-10,3.,3.])))
# tensor([ True, False,  True])

• torch.all(input)
  torch.all(input):测试输入中的所有元素的值是否为True。如果所有的值为True，则返回True,否则返回False

# import library
import torch# define the tensor a , b
a = torch.Tensor([1,0,2,0])
b = torch.Tensor([1,2,3,4,5])# convert the values into boolean type
b_bool = b.bool()
a_bool = a.bool()# if all the values in tensor a_all is true ,it return the final answer for True
# if just including the one False value in tensor a_all,it return the final answer for False
a_all = torch.all(a_bool)
b_all = torch.all(b_bool)
print(f"a={a}")
print(f"a_bool={a_bool}")
print(f"a_all={a_all}")
print("*"*50)
print(f"b={b}")
print(f"b_bool={b_bool}")
print(f"b_all={b_all}")

a=tensor([1., 0., 2., 0.])
a_bool=tensor([ True, False,  True, False])
a_all=False
**************************************************
b=tensor([1., 2., 3., 4., 5.])
b_bool=tensor([True, True, True, True, True])
b_all=True

• torch.equal()&torch.eq(a,b)
  torch.eq(a,b):计算张量a和b中每个对应位置的值是否相等，并返回每个位置的True 和 False
  torch.equal(a,b):比较张量a,b在形状和值是否相等，返回整体的True 和False

# import the library
import torch# define the variable tensor a and b
a = torch.Tensor([[1,2,3],[4,5,6]])
b = torch.Tensor([[1,4,2],[2,3,6]])# compare the values of the each elements in tensor a and b is whether equal
c_eq = torch.eq(a, b)# just compare the tensor a and b is whether equal
d_equal = torch.equal(a,b)
print(f"a={a}")print(f"b={b}")print(f"c_eq={c_eq}")print(f"d_equal={d_equal}")

a=tensor([[1., 2., 3.],[4., 5., 6.]])
b=tensor([[1., 4., 2.],[2., 3., 6.]])
c_eq=tensor([[ True, False, False],[False, False,  True]])
d_equal=False

3. Resnet 算子融合

3.1 目标

将Resnet模块中
$$resul{t}_1=conv3\times 3+conv1\times 1+x$$

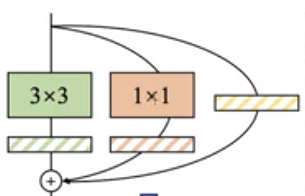
转换成：
$$resul{t}_2=conv3\times 3+conv3\times 3+conv3\times 3$$

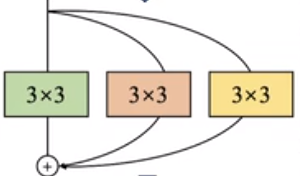
最后我们在使用的时候用一个3×3卷积表示即可得到result1的同等效果，达到算子融合的目的

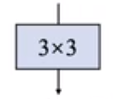
3.2 步骤

• 将1×1卷积改造成3×3卷积conv_2d_for_pointwise
• 将x本身改造成3×3卷积conv_2d_for_identity
• 创建一个新的融合3×3卷积conv_2d_for_fusion
• 将conv_2d_for_pointwise，conv_2d_for_identity和本来就有的3×3卷积conv2d权重和偏置相加后赋值给conv_2d_for_fusion
• conv_2d_for_fusion.weight = conv2d.weight + conv_2d_for_pointwise.weight + conv_2d_for_identity.weight
• conv_2d_for_fusion.bias = conv2d.bias + conv_2d_for_pointwise.bias + conv_2d_for_identity.bias
• 这样我们就得到一个新的卷积conv_2d_for_fusion;它满足了resnet的所有需求，而且更快

3.3 代码

import torch
from torch import nn
import torch.nn.functional as F
import timein_channels = 2
ou_channels = 2
kernel_size = 3
w = 9
h = 9
t1 = time.time()
# 方法1：原生写法
x = torch.ones(1, in_channels, w, h)
conv_2d = nn.Conv2d(in_channels, ou_channels, kernel_size, padding="same")
conv_2d_pointwise = nn.Conv2d(in_channels, ou_channels, 1)result1 = conv_2d(x) + conv_2d_pointwise(x) + x
t2 = time.time()
# 方法2：算子融合
# 把 point_wise 卷积核 x 本身都携程 3*3 的卷积
# 最终把三个卷积写成一个卷积实现算子融合# step 1: 将 1x1的卷积转换成 3x3 的卷积
# conv_2d_pointwise.weight.shape = (2,2,1,1) 通过填充变成 (2,2,3,3)pointwise_to_conv_weight = F.pad(conv_2d_pointwise.weight, [1, 1, 1, 1, 0, 0, 0, 0])
conv_2d_for_pointwise = nn.Conv2d(in_channels, ou_channels, kernel_size, padding="same")
conv_2d_for_pointwise.weight = nn.Parameter(pointwise_to_conv_weight)
conv_2d_for_pointwise.bias = nn.Parameter(conv_2d_pointwise.bias)# step 2： 将 x 本身转换成 3x3 的卷积
#       x 经过 3x3 的卷积conv_2d_for_identity还是能够保证值不变
# 为了保证 x 在转换过程中的值不变，需要满足如下两个条件
# 1. 3x3的卷积不能在像素与像素之间具有关联性
#    需要一个 3x3 矩阵，中心为1，其他为0
# 2. 3x3的卷积不能在通道与通道之间具有关联性
#    需要通道上面[中间1矩阵，全0矩阵，全0矩阵，中间1矩阵]；这样通道间就没关联了
#    卷积的形状为：（2，2，3，3）;我们需要定义卷积的weights和bias来实现自定义卷积
#conv_2d_for_identity = nn.Conv2d(in_channels, ou_channels, kernel_size, padding="same")
zeros = torch.unsqueeze(torch.zeros(kernel_size, kernel_size), 0)
stars = torch.unsqueeze(F.pad(torch.ones((1, 1)), [1, 1, 1, 1]), 0)
zeros_stars = torch.unsqueeze(torch.cat([zeros, stars], 0), 0)
stars_zeros = torch.unsqueeze(torch.cat([stars, zeros], 0), 0)
conv_2d_for_identity_weight = torch.cat([zeros_stars, stars_zeros], dim=0)
conv_2d_for_identity_bias = torch.zeros([ou_channels])
conv_2d_for_identity.weight = nn.Parameter(conv_2d_for_identity_weight)
conv_2d_for_identity.bias = nn.Parameter(conv_2d_for_identity_bias)result2 = conv_2d(x) + conv_2d_for_pointwise(x) + conv_2d_for_identity(x)# result2 = conv_2d_for_pointwise(x)
# result2 = conv_2d_for_identity(x)
# print(f"torch.all(torch.isclose(result1,result2))\t=\t{torch.all(torch.isclose(result1,result2))}")
# print(f"zeros={zeros}")
# print(f"zeros.shape={zeros.shape}")
# print(f"stars.shape={stars.shape}")
# print(f"stars={stars}")
# print(f"zeros_stars={zeros_stars}")
# print(f"zeros_stars.shape={zeros_stars.shape}")# step 3： 将改造后的矩阵conv_2d(x)；conv_2d_for_pointwise(x)；conv_2d_for_identity(x)进行融合conv_2d_for_fusion = nn.Conv2d(in_channels, ou_channels, kernel_size, padding="same")
conv_2d_for_fusion.weight = nn.Parameter(conv_2d.weight.data + conv_2d_for_pointwise.weight.data + conv_2d_for_identity.weight.data)
conv_2d_for_fusion.bias = nn.Parameter(conv_2d.bias.data + conv_2d_for_pointwise.bias.data + conv_2d_for_identity.bias.data)result3 = conv_2d_for_fusion(x)
t3 = time.time()# print(f"torch.all(torch.isclose(result1,result3))\t=\t{torch.all(torch.isclose(result1,result3))}")print(f"原生卷积 time = {1000*(t2-t1)}ms")
print(f"融合卷积 time = {1000*(t3-t2)}ms")

结果：

原生卷积 time = 1.9557476043701172ms
融合卷积 time = 0.9968280792236328ms

3.4 小结

多次实验，我们在不改变值的情况下，我们发现，经过算子融合的网络即使在python这样的语法下，也能在运行速度上提高2倍；其主要思想还是像地铁思想样，我们从A点到B点，如果有三个人甲，乙，丙 ；他们如果单独进行运动，那么时间就会长，如果我们将甲乙丙三个人打包到地铁上，让他们搭载地铁，那么他们一起到达B点的时间就会缩短。

这篇关于16 - nn.Conv2d的原理以及三路分支残差block的算子融合实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---