推荐算法模型 ----- Attentional Factorization Machines 论文阅读笔记

本文主要是介绍推荐算法模型 ----- Attentional Factorization Machines 论文阅读笔记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

论文名字：Attentional Factorization Machines:Learning the Weight of Feature Interactions via Attention Network
论文地址：http://staff.ustc.edu.cn/~hexn/papers/ijcai17-afm.pdf
若有错误或不足，烦请各位dalao指教

AFM模型提出的目的和背景

AFM也是一个典型的基于FM思想提出的模型，我们知道为了解决辛普森悖论问题，需要对不同的特征进行组合，但是这些特征组合对最后模型的性能的影响各不相同，所以为了提升模型的预测结果，AFM提出一种attention结构，让对结果有很大促进的特征组合有更大的权值。

AFM的模型结构

在这里插入图片描述
总体的结构就是这个样子，是不是很面熟，这个和NFM模型的结构很类似，只不过NFM在做Bi-interaction之后就直接接入DNN了，而AFM多了一个Attention-based Pooling，并且AFM后面也没有接入深层网络，而是直接做weight sum后再接一个线性映射就输出了，线性映射部分图中其实是省略掉了。

Input & Embedding Layer

AFM和NFM一样，都是对二阶特征组合方程部分进行建模，首先输入部分依然是稀疏特特征和稠密特征concat一起的长向量，这里需要说明一下，关于数值型特征如何参与特征组合，一开始我也没明白，看了很多博客之后，有一位dalao解释的很清楚（附上传送门：传送门）

Pair-wise Interaction Layer

其实，这部分做的工作就是做特征组合，具体的方法如下：
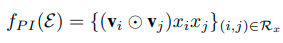
在这里插入图片描述
这个 $\odot$ 的意思就是，两个向量对应元素相乘，显然最后的结果仍然是个向量，假设我们有m个特征，最后组合结束之后就会得到 $\frac{m(m-1)}{2}$ 个组合向量

Attention-based Pooling Layer

这部分其实就相当于NFM在Bilinear interaction layer之后做sum pooling之后在接一个全连接层的操作，文中给出的公式如下：
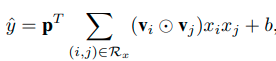
在这里插入图片描述
这个 $P$ 就是全连接层的参数，作者指出，如果 $P$ 的所有值都为1，并且b为0，这个就是FM的二阶交叉项，我来给大家推导一下：

所以这种结构可以看作是扩展的FM。这样的话可以将向量转化为最后二阶特征组合的分数值（这里注意一下，这个 $P$ 不是attention score，仅仅是一个映射的权重向量而已），而AFM是要在sum pooling操作的时候，学习一个权重 $\alpha_{ij}$ ，表达式如下所示：
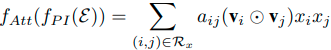
在这里插入图片描述
文中说，这个权重可以直接通过梯度下降去硬学，但是会有问题，和FM的 $w_{ij}$ 一样，如果这两个特征组合从来都没在训练集里出现过，那这个权重就学不到了，为了解决这个问题，AFM提出了一个Attention Network的结构，其实就一层而已，具体的表达如下：
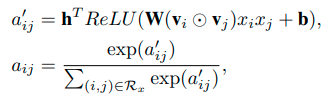
在这里插入图片描述
这个结构其实就是把每个组合后的特征向量作为样本输入到网络里，通过一个全连接层使用Relu作为激活函数，再通过一个线性映射将向量转换为数值，具体的网络结构应该如下所示：

最后的这个值要过一个softmax函数转换为概率（其实这里小弟是有疑惑的，一开始我在想，多个特征组合的向量通过这个attention network是否共享这个W呢？看了几位dalao的代码发现，应该是共享W的），最后AFM的计算公式就变成了下面这个样子：
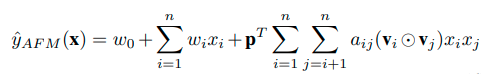
在这里插入图片描述
前面的那个 $\hat{y}$ 里面的b可能合并到偏差 $w_0$ 里面了。

Some Problem

AFM也存在过拟合问题，文中提到为了解决隐藏层不同单元依赖过高的问题，在pair-wise interaction layer加入dropout层（什么是co-adaptations可以看看这篇文章传送门），同时在attention network上加了L2正则化，最终的loss公式如下（以回归问题为例）：
在这里插入图片描述
作者提出，没有在attention network里使用dropout的原因是稳定性的问题，同时使用两个dropout层，模型的稳定性变差，影响性能。

实验结果

实验的数据集采用Frappe和MovieLens，评价指标采用的RMSE，为了平衡正负样本的比例，作者每个正样本就随机匹配两个负样本。同时，作者将数据集按7:2:1划分，70%的训练集，20%的验证集（用来调整超参数），10%的测试集用来做对照实验。Baseline为FM（使用LibFM工具包实现），high-order FM（使用HOFM工具包实现），Wide&Deep和DCN，为了验证AFM的效果，作者提出了三个问题：
RQ1:dropout和l2正则化对结果真的有影响吗？效果如何？
RQ2:attention network能不能学习到不同特征组合的权重呢？（就是看AN有没有用）
RQ3:与SOTA相比，AFM有没有提升

超参数设计

优化方法使用adagrad，batch-sized大小设为：Frappe（128），MovieLens（4096），embedding-size设为256，attention-factor设为256（attention-factor就是上文提到的attention-network里的隐藏层的维度），为了防止过拟合，作者还使用了early-stop的策略，同时用FM的embedding结果初始化wide&deep和DCN

超参数结果

在这里插入图片描述
以LibFM的结果作为基线，可以看到加Dropout后确实对结果有所提升，而且实验结果表示，不同的数据集有不同的最优dropout-ratio，而且作者提到文中实现的FM（后面简称为vFM）比LibFM性能好的原因有两点：(1) vFM使用dropout作为正则化的方法而不是l2 (2) vFM使用Adagrad而非SGD（自适应学习率）
在这里插入图片描述
为了验证L2正则化对AFM结果的影响，作者固定dropout为最优值，将 $\lambda$ 从0调整到16，最后的结果如上图所示，看到AFM的RMSE的值仍然在下降，说明L2正则化是有效果的

接下来要寻找最优的attention-factor的值，如下图所示：
在这里插入图片描述
可以看到无论t取多少，这个模型的结果都很稳定，一个极端情况就是取1，那么attention-network的参数W就变成了一个向量，这样整个attention-network就变成了线性变换，但是我们可以看到AFM的结果依然要比FM好很多，这也说明了attention-component的重要性，同时作者记录每20个epoch的loss，如下图所示：
在这里插入图片描述
可以看到，AFM收敛的比FM快，而且效果更好

Micro-level analysis

还是为了验证attention network的重要性，作者将attention-score引入到FM当中，并且固定所有的 $\alpha_{ij}= \frac{1}{R_x}$ ，首先使用FM训练embedding然后固定这个embedding只训练attention-network部分，然后选择三个正样本（target为1），抽出三个特征组合的attention-score进行分析，如下图所示：
在这里插入图片描述
以第一个样本为例，可以看到FM所有的attention-score都是一样的，但是显然item-tag的特征组合对结果是更有效果的，而AFM对于不同的特征组合有不同的权重，并且对结果有促进作用的权重更大，反之权重小一些，从而证明了attention-network的有效性，而且加入attention-score之后，模型的可解释性就更强。