人工智能系列实验（一）——用于识别猫的二分类单层神经网络

本实验利用Python，搭建了一个用于识别猫的单神经元神经网络，最终实现在测试集上的准确率在70%以上。

实验环境： python中numpy、matplotlib、h5py和skimage库

import numpy as np
import matplotlib.pyplot as plt  # 用于画图
import h5py  # 用于加载训练数据集
import skimage.transform as tf  # 用于缩放图片

训练样本： 209张64*64的带标签图片

测试样本： 50张64*64的带标签图片

关于本实验中所用数据集与完整代码详见：
https://github.com/PPPerry/AI_projects/tree/main/1.cats_identification

构建的神经网络模型如下：

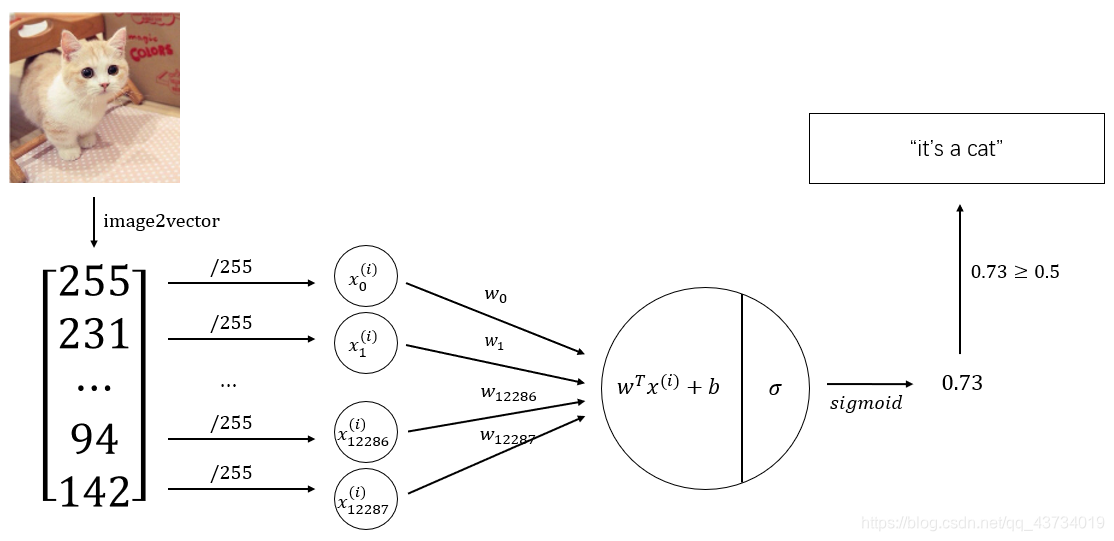
基于该神经网络模型，代码实现如下：

首先，对数据集数据进行预处理。

def load_dataset():"""加载数据集数据:return: 训练数据与测试数据的相关参数"""train_dataset = h5py.File("datasets/train_catvnoncat.h5", "r")train_set_x_orig = np.array(train_dataset["train_set_x"][:])  # 提取训练数据的特征数据，格式为(样本数, 图片宽, 图片长, 3个RGB通道)train_set_y_orig = np.array(train_dataset["train_set_y"][:])  # 提取训练数据的标签数据，格式为(样本数, )test_dataset = h5py.File("datasets/test_catvnoncat.h5", "r")test_set_x_orig = np.array(test_dataset["test_set_x"][:])  # 提取测试数据的特征数据test_set_y_orig = np.array(test_dataset["test_set_y"][:])  # 提取测试数据的标签数据classes = np.array(test_dataset["list_classes"][:])  # 提取标签，1代表是猫，0代表不是猫train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))  # 统一类别数组格式为(1, 样本数)test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))return train_set_x_orig,  train_set_y_orig, test_set_x_orig, test_set_y_orig, classestrain_set_x_orig,  train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()  # 加载数据集数据m_train = train_set_x_orig.shape[0]  # 训练样本数
m_test = test_set_x_orig.shape[0]  # 测试样本数
num_px = test_set_x_orig.shape[1]  # 正方形图片的长/宽train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T  # 将样本数据进行扁平化和转置，格式为(图片数据, 样本数)
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).Ttrain_set_x = train_set_x_flatten/255.  # 标准化处理，使所有值都在[0, 1]范围内
test_set_x = test_set_x_flatten/255.

其次，构造神经网络中用到的相应函数。
其中，前向传播的公式为
$$\begin{array}{c}A=\sigma (w^{T}X+b)=(a^{(1)},a^{(2)},\cdots ,a^{(m-1)},a^{(m)})\\ \\ J=-\frac{1}{m}{\sum }_{i=1}^{m}log(a^{(i)})+(1-y^{(i)})log(1-a^{(i)})\end{array}$$
反向传播的公式为
$$\begin{array}{c}\frac{\partial J}{\partial w}=\frac{1}{m}X(A-Y{)}^T\\ \\ \frac{\partial J}{\partial b}=\frac{1}{m}{\sum }_{i=1}^m(a^{(i)}-y^{(i)})\end{array}$$

def sigmoid(z):"""sigmod函数实现:param z: 数值或一个numpy数组:return: [0, 1]范围数值"""s = 1 / (1 + np.exp(-z))return sdef initialize_with_zeros(dim):"""初始化权重数组w和偏置b为0:param dim: 权重值的数量:return:w: 权重数组b: 偏置bias"""w = np.zeros((dim, 1))b = 0return w, bdef propagate(w, b, X, Y):"""实现正向传播和反向传播，分别计算出成本与梯度:param w: 权重数组:param b: 偏置:param X: 图片的特征数据:param Y: 图片的标签数据:return:cost: 成本dw: w的梯度db：b的梯度"""m = X.shape[1]# 前向传播A = sigmoid(np.dot(w.T, X) + b)cost = -np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A)) / m# 反向传播dZ = A - Ydw = np.dot(X, dZ.T) / mdb = np.sum(dZ) / m# 梯度保存在字典中grads = {"dw": dw,"db": db}return grads, costdef optimize(w, b, X, Y, num_iterations, learning_rate, print_cost=False):"""梯度下降算法更新参数:param w: 权重数组:param b: 偏置bias:param X: 图片的特征数据:param Y: 图片的标签数据:param num_iterations: 优化迭代次数:param learning_rate: 学习率:param print_cost: 为真时，每迭代100次，打印一次成本:return:params: 优化后的w和bcosts: 每迭代100次，记录一次成本"""costs = []for i in range(num_iterations):grads, cost = propagate(w, b, X, Y)dw = grads["dw"]db = grads["db"]# 梯度下降w = w - learning_rate * dwb = b - learning_rate * db# 记录成本变化if i % 100 == 0:costs.append(cost)if print_cost:print("优化%d次后成本是：%f" % (i, cost))params = {"w": w,"b": b}return params, costsdef predict(w, b, X):"""预测函数，判断是否为猫:param w: 权重数组:param b: 偏置bias:param X: 图片的特征数据:return:Y_predicition: 预测是否为猫，返回值为0或1p: 预测为猫的概率"""m = X.shape[1]Y_prediction = np.zeros((1, m))p = sigmoid(np.dot(w.T, X) + b)for i in range(p.shape[1]):if p[0, i] >= 0.5:Y_prediction[0, i] = 1return Y_prediction, p

最终，组合以上函数，构建出最终的神经网络模型函数。

def model(X_train, Y_train, X_test, Y_test, num_iterations=2001, learning_rate=0.5, print_cost=False):"""最终的神经网络模型函数:param X_train: 训练样本的特征数据:param Y_train: 训练样本的标签数据:param X_test: 测试样本的特征数据:param Y_test: 测试样本的标签数据:param num_iterations: 优化迭代次数:param learning_rate: 学习率:param print_cost: 为真时，每迭代100次，打印一次成本:return:d: 返回相关信息的字典"""w, b = initialize_with_zeros(X_train.shape[0])  # 初始化参数parameters, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)  # 训练参数w = parameters["w"]b = parameters["b"]Y_prediction_train, p_train = predict(w, b, X_train)Y_prediction_test, p_test = predict(w, b, X_test)print("对训练数据的预测准确率为：{}%".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))print("对测试数据的预测准确率为：{}%".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))d = {"costs": costs,"Y_prediction_test": Y_prediction_test,"Y_prediction_train": Y_prediction_train,"w": w,"b": b,"learning_rate": learning_rate,"num_iterations": num_iterations,"p_train": p_train,"p_test": p_test}return d

现在调用上面的模型函数对我们最开始加载的数据进行训练。

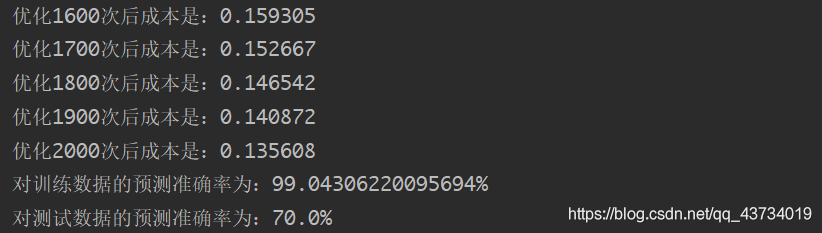
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations=2001, learning_rate=0.005, print_cost=True)

输出：优化2000次后的成本是0.1356。对训练数据的准确率为99%左右，对测试数据的准确率为70%左右。

试验模型预测功能：

1. 查看训练集和测试集中图片及其对应的预测结果

def show_predict(index, prediction=np.hstack((d["Y_prediction_train"], d["Y_prediction_test"])),data=np.hstack((train_set_x, test_set_x)), origin=np.hstack((train_set_y, test_set_y)),px=num_px, p=np.hstack((d["p_train"], d["p_test"]))):if index >= prediction.shape[1]:print("index超出数据范围")returnplt.imshow(data[:, index].reshape((px, px, 3)))plt.show()print("这张图的标签是" + str(origin[0, index]) + "，预测分类是" + str(int(prediction[0, index])) + "，预测概率是" + str(p[0, index]))return

以第19张图片为例：

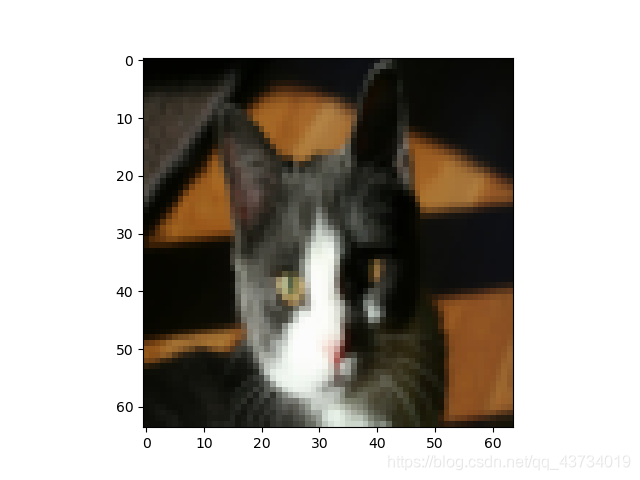
输出：这张图的标签是1，预测分类是1，预测概率是0.93。

2. 查看自己输入的图片及其对应的预测结果

# 预测自己的图片
# 在同目录下创建一个文件夹images,把你的任意图片改名成my_image1.jpg后放入文件夹
my_image = "my_image1.jpg"image = np.array(plt.imread(my_image))
my_image = tf.resize(image, (num_px, num_px), mode='reflect').reshape((1, num_px*num_px*3)).T
my_prediction, my_p = predict(d["w"], d["b"], my_image)plt.imshow(image)
plt.show()
print("预测分类是" + str(int(my_prediction[0, 0])) + "，预测概率是" + str(my_p[0, 0]))

以下图为例：

输出：预测分类是1，预测概率是0.89。

进一步实验得到的结论：

1. 成本随迭代次数增加时的变化情况

# 绘制成本随迭代次数增加时的变化情况
costs = np.squeeze(d['costs'])  # 将表示向量的数组转换为秩为1的数组，便于matplotlib库函数画图
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()

结论：训练次数越多，成本越小，预测结果越精确。

2. 不同学习率下成本随迭代次数增加时的变化情况

# 绘制在不同学习率下成本随迭代次数增加时的变化情况
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations=2001, learning_rate=i,print_cost=False)for i in learning_rates:plt.plot(np.squeeze(models[str(i)]["costs"]), label=str(models[str(i)]["learning_rate"]))plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
legend = plt.legend(loc='upper right', shadow=True)
plt.show()

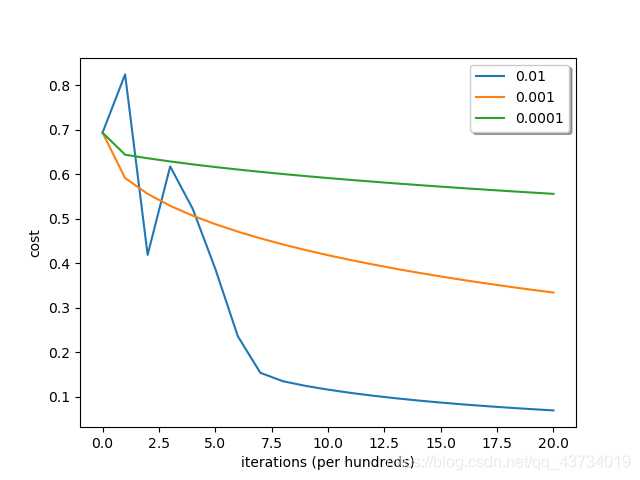
结论：选择一个正确的学习率很重要，不一定越大越好。设置不合理，神经网络有可能永远都不能下降到损失函数的最小值处；相反，设置合理，可以使神经网络的收敛达到很好的效果。

结束语：

1. 实验过程中，一定要搞清楚变量的维度，否则做数据处理、写数组操作时会容易出现问题。
2. 数据集、图片等需要和代码在同一目录下。
3. 本实验几乎基于纯Python的numpy库函数进行神经网络模型的搭建，没有使用任何机器学习框架，重在理解数学原理及意义。在后续的实验中，我会对TensorFlow等经典框架进行学习与运用。
4. 相关代码可能会不断更新改进，以github中的代码为准。
5. 这是我在系统学习人工智能中实现的第一个人工智能程序，后续还会不断更新系列实验。写博客以督促自己不能总摸鱼233，希望自己能在神经网络这条路上走的尽可能远一些。