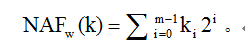本文主要是介绍OpenSSL密码库算法笔记——第5.4.11章 椭圆曲线的多倍点运算——未知点,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本小节来讨论kP的计算方法,这里的P为椭圆曲线上的点,k为一个整数。这个运算就是多倍点运算,它是椭圆曲线密码算法的核心。设曲线的阶为#E(Fp)=nh,其中n为素数,是点P在椭圆曲线上的阶,h为相伴因子,是一个很小的数,k∈[1, n-1]。
多倍点计算主要是通过对k的不同表示来实现的。有对k进行二进制展开的平方和算法(平方和算法的思想参见§4.1.1);有对k进行NAF展开的二进制NAF算法;有结合NAF和窗口算法的wNAF算法(窗口算法的思想参见§4.1.2)。下面将重点介绍高效的wNAF算法。
wNAF算法中的NAF是一种表示形式,而w表示的是窗口算法的宽度。
具体说来,NAF是系数k的一种“不相邻表示形式”【non-adjacent form】,简称NAF,它将k表示成带符号的比特形式k=∑ki2i,这里的ki ∈{0, ±1}。任一正整数k都有唯一一个NAF表示形式,记为NAF(k)。NAF展开式要求任意连续的两个比特中最多只能有一个比特非零,即不可能出现连续的两个比特都非零的情况。NAF表示的长度最多比二进制表示的长度多1,且其非零比特数将减少。如果将非零比特数和全部比特数的比值称为密度,则NAF展开的密度为1/3,比二进制展开的密度1/2小。
例如39的二进制展开形式为(1, 0, 0, 1, 1, 1),如用NAF展开则得到NAF(39)=(1, 0, 1, 0, 0, -1)。
既然窗口算法的思想可以用在二进制展开中(见§4.1.2),那为什么不能将窗口算法的思想用在NAF展开形式中呢?由此,就有了wNAF展开形式。它将k表示成带符号的“比特”形式k=∑ki2i,这里的ki为奇数且| ki | < 2w-1,w是窗口大小。同样地,任一正整数k都有唯一一个wNAF表示形式,记为NAFw(k),且NAF2(k)=NAF(k)。wNAF展开要求任意连续的w个比特中最多只能有一个比特非零。与NAF表示一样,wNAF展开的长度最多比二进制的长度多1。wNAF展开的密度为1/(w+1),相比之下,NAF展开的密度为1/3,二进制展开的密度为1/2。计算wNAF展开形式的算法如下:

Step2.1中的k mods 2w是指k模2w的(可负)最小剩余u,即
…………(5.13)
下面来看看wNAF算法怎样用于多被点的计算之中。设系数k的wNAF展开已经计算出来。
首先,预计算出一些点:Pi ←iP,i=1, 3, 5, …, 2w-1-1;然后,再类似于窗口算法那样计算kP。具体算法如下。

在预计算Step1中需要花费1D+2w-2A,这里的D表示二倍点运算,A表示点的普通加法;在Step3中需要花费mD+m/(w+1)A。
实现代码中做多倍点计算时采用的就是这个wNAF算法。
───────────────────────────────────────
int EC_POINTs_mul(const EC_GROUP *group, EC_POINT *r, const BIGNUM *scalar, size_t num, const EC_POINT *points[], const BIGNUM *scalars[])
功能: 多个点的多倍点运算
输入: group,scalar,num【点points []的个数】,points[],scalars[]
输出: r ← scalar×group->generator+(scalars[0]×points[0]+scalars[1]×points[1]+……)
返回: 1【正常】 or 0【出错】
出处: ec_lib.c
调用: ▼ int ec_wNAF_mul(const EC_GROUP *group, EC_POINT *r, const BIGNUM *scalar, size_t num, const EC_POINT *points[], const BIGNUM *scalars[])
备注: 调用的ec_wNAF_mul采用的是wNAF算法,但不同的点采用的宽度可能不同。
───────────────────────────────────────
特别地,当点points []的个数num退化为1的时候,即
![]() , ……(5.14)
, ……(5.14)
就可以使用简化形式:
───────────────────────────────────────
int EC_POINT_mul(const EC_GROUP *group, EC_POINT *r, const BIGNUM *g_scalar,const EC_POINT *point, const BIGNUM *p_scalar)
功能: 两个点的多倍点运算
输入: group,g_scalar,point,p_scalar
输出: r ←g_scalar×group->generator+p_scalar×point
返回: 1【正常】 or 0【出错】
出处: ec_lib.c
调用: ▼ int EC_POINTs_mul(const EC_GROUP *group, EC_POINT *r, const BIGNUM *scalar, size_t num, const EC_POINT *points[], const BIGNUM *scalars[])
───────────────────────────────────────
这篇关于OpenSSL密码库算法笔记——第5.4.11章 椭圆曲线的多倍点运算——未知点的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!