未知专题

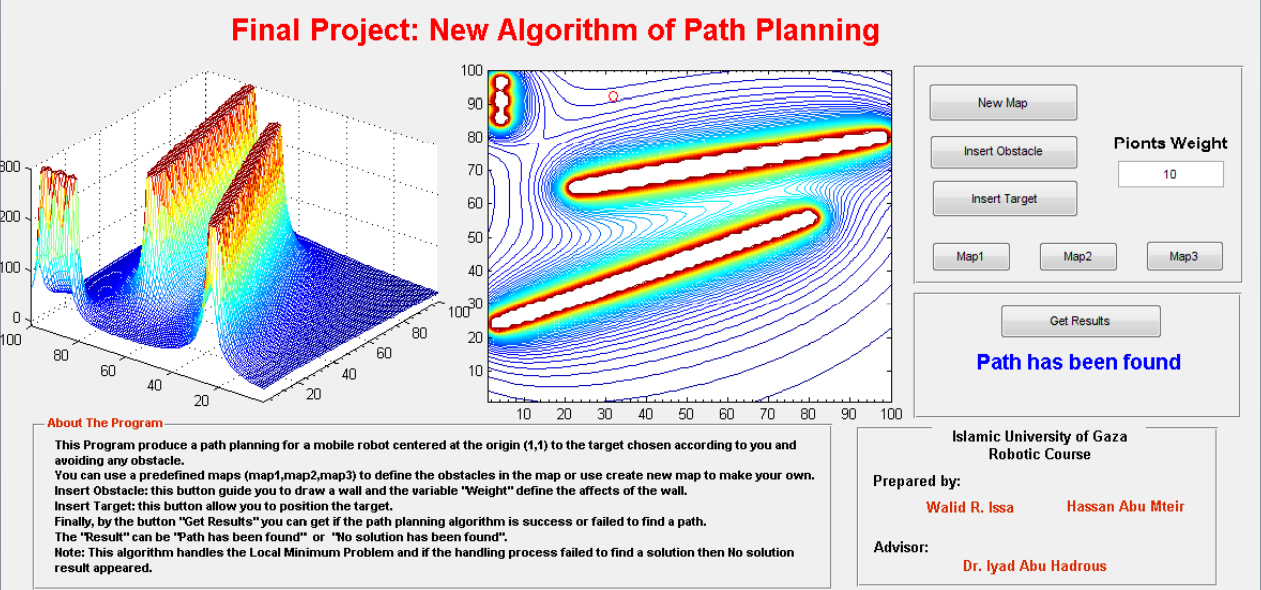
【路径规划】移动机器人在未知环境下目标的路径规划算法

摘要本文介绍了一种新型路径规划算法，专用于在包含多个障碍物的环境中为机器人找到最优路径。该算法通过分析障碍物位置和目标点位置，生成一个引导机器人避开障碍物并到达目标的路径。项目展示了路径规划在机器人导航中的重要性，并通过实验验证了算法的有效性。理论路径规划是机器人导航的核心技术，旨在寻找从起点到目标点的最优路径，避开环境中的障碍物。本文提出的算法通过以下步骤实现路径规划： 1.

Ubuntu12下未知驱动器处理

一、背景在挂载大硬盘（Ubuntu12下挂载硬盘（9TB））的过程出现了错误导致下图的错误：Ubuntu下使用pvdisplay命令发现有未知驱动器的信息：Couldn’t find device with uuid ‘xxxxxxxxxxxxx’，如下图所示：（图1：unknown device）如果出现上面的错误，是没有办法按照Ubuntu12下挂载硬盘（9TB）的步骤进行

反事实推理（Counterfactual Reasoning）：探索未知与决策的桥梁

反事实推理（Counterfactual Reasoning）：探索未知与决策的桥梁反事实推理（Counterfactual Reasoning）是一种思维方式，它试图回答“如果……会怎样？”的问题。简单来说，反事实推理是在已有事实的基础上，通过假设条件发生改变，来推测可能的结果。我们可以通过这个过程更好地理解因果关系，并帮助我们在未来做出更好的决策。 1. 反事实推理的基本原理反事

从CSS注入到渗透未知网页

简介这篇文章中，分享一个技巧。通过CSS注入盲打用户前端页面敏感数据需要的前提：存在CSS注入漏洞的环境理论最高危害：1 click用户接管环境记录采取docker-compose 部署部署nginx-docker mkdir nginx_testcd nginx_testtouch docker-compose.ymlmkdir -p nginx/c

概率统计Python计算：一元线性回归未知参数的区间估计

在博文《一元线性回归未知参数的点估计》中利用scipy.stats的linregress函数，计算了总体分布 N ( a x + b , σ 2 ) N(ax+b, \sigma^2) N(ax+b,σ2)的未知参数 a a a， b b b和 σ 2 \sigma^2 σ2的无偏估计 a ∧ \stackrel{\wedge}{a} a∧， b ∧ \stackrel{\wedge}{b} b

概率统计Python计算：一元线性回归未知参数的点估计

设试验结果可表为随机变量 Y Y Y，影响试验结果 Y Y Y的因素是可控的且表为普通变量 x x x，若 Y Y Y~ N ( a x + b , σ 2 ) N(ax+b,\sigma^2) N(ax+b,σ2)，其中 a , b a,b a,b即 σ 2 \sigma^2 σ2均为未知参数。对 x x x的一系列取值 ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cd

qt [error C3646: 未知重写说明符]错误的可能性

1.循环引用在分离式编译中，我们往往习惯将不同的类或者函数分别写在不同的函数中，提高工作效率。但如果在使用时出现两个类分别在两个不同的文件中编写，并且相互引用，则会出现循环引用，引发此错误。举例：one.h/one.cpp和two.h/two.cpp 在one.h中include two.h，并定义了一个two的object，然后在two.h中又include了one.h 解决方案

oracle10g安装未知错误

昨天低格系统后在Windows7下安装Oracle 10g提示“程序异常终止，发生未知错误”。我的解决方法：右键setup.exe，属性->兼容性->以兼容模式运行这个程序 windows xp（ service pack 3），以管理员身份运行安装就可以了。

(c#)AutoCAD二次开发调试时，netload后，输入命令，却显示为未知命令

版本： Visual Studio 2015 AutoCAD 2017 1、先确认一点，引用的.dll文件的属性--“”“复制本地”，是否为False 2、菜单栏-调试-XXXXX属性--启用本机代码调试(重点就是这个要勾选)，倘若不勾选的话，就会出现输入的命令为“”未知命令“”，这个是导致问题出现的关键，本次问题的源头！！ 2016.08.25 今日发现

5、catch中发生了未知异常，finally代码块如何应对？

catch中发生了未知异常，finally还会执行么？ catch发生了异常，finally还是会执行的，并且是finally执行完成后，才会抛出catch中的异常。不过catch会吃掉try中抛出的异常，为了避免这种情况，在一些可以预见catch中会发生异常的地方，先把try抛出的异常打印出来，这样从日志中就可以看到完整的异常信息。

一年前 LLM AGI 碎片化思考与回顾系列⑤ · 探索SystemⅡ复杂推理的未知之境

阅读提示：本篇系列内容的是建立于自己过去一年在以LLM为代表的AIGC快速发展浪潮中结合学术界与产业界创新与进展的一些碎片化思考并记录最终沉淀完成，在内容上，与不久前刚刚完稿的那篇10万字文章「融合RL与LLM思想，探寻世界模型以迈向AGI」间有着非常紧密的联系，可以说，这篇长篇文章中的很多内容也是基于这些碎片化的思考与沉淀，当然也正是这样的一个个碎片化的、看似玄幻大胆、step by

Web前端设计入门：探索未知，点亮创意之光

Web前端设计入门：探索未知，点亮创意之光在数字化浪潮汹涌的时代，Web前端设计作为连接用户与数字世界的桥梁，其重要性日益凸显。对于初学者来说，如何快速入门并掌握这一技能，成为了一个充满挑战与机遇的课题。本文将从四个方面、五个方面、六个方面和七个方面，带领大家探索Web前端设计的奥秘，点亮创意之光。四个方面：Web前端设计的基本概念与技能 Web前端设计，简而言之，就是通过HTML、CS

TypeScript未知泛型——unknown和any

在 TypeScript 中，如果你想要表示一个泛型变量，但你不知道或不关心它具体是什么类型，你可以使用 any 类型。然而，any 类型会绕过类型检查，这可能不是你想要的。为了保持类型安全性，TypeScript 提供了一个特殊的类型 unknown，它可以用来表示任何类型的值，但在使用之前需要进行类型检查或类型断言。 unknown 类型示例： function processVal

科幻巨制《荒野》：未知世界等你挑战

2024年春季影视新潮流随着2024年春季的到来，影视圈也迎来了一股清新的潮流。最新上映的《破墓》由崔岷植、金高银等实力派演员主演，悬疑揭秘，你敢看真相吗？惊悚悬疑的剧情让人欲罢不能。而科幻巨制《荒野》则带领观众探索未知的科幻世界，紧张刺激的节奏让人心跳加速。与此同时，喜剧电影《末路狂花钱》以幽默诙谐的方式讲述了一段搞笑的故事，让观众在欢笑中感受到生活的美好

exe语言编程：深入探索与挑战未知

exe语言编程：深入探索与挑战未知在编程的浩瀚宇宙中，exe语言编程无疑是一个充满神秘与挑战的领域。它不仅仅是一种技能，更是一种艺术，需要我们用心去揣摩、去实践。那么，exe语言编程究竟是什么呢？本文将从四个方面、五个方面、六个方面和七个方面，带领大家深入探索这个神秘的领域。四个方面：exe语言编程的基本概念与特点首先，我们需要了解exe语言编程的基本概念。exe，即可执行文件，是计算

AI大模型:掌握未知，开启未来

AI大模型的工作原理 AI大模型是指通过大量数据和复杂算法训练出的能够理解和生成自然语言文本的人工智能模型。它们背后的核心技术主要包括深度学习、神经网络和自然语言处理。以下是详细的工作原理以及通俗易懂的类比： 1. 数据收集和预处理 AI大模型的训练首先需要大量的数据，这些数据可以是文本、图片、音频等形式。对于语言模型来说，主要是大量的文本数据。这些数据需要经过预处理，比如清洗、去重、标注等

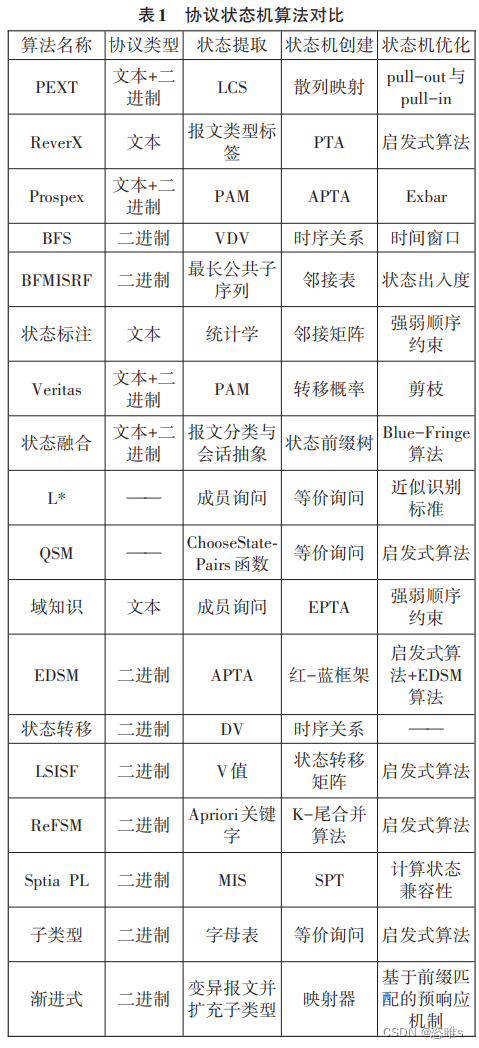
阅读笔记——《未知协议状态机推断技术研究综述》

【参考文献】盛嘉杰, 牛胜杰, 陈阳, 等. 未知协议状态机推断技术研究综述[J]. 计算机与现代化, 2023 (05): 58.【注】本文仅为作者个人学习笔记，如有冒犯，请联系作者删除。摘要协议逆向工程（PRE）描述了协议的行为逻辑，一般分为协议格式提取和状态机构造2个步骤。首先，本文介绍PRE的形式化定义和基本原则，并讨论主要领域的具体要求。其次，分析状态机推理方法，并将其分

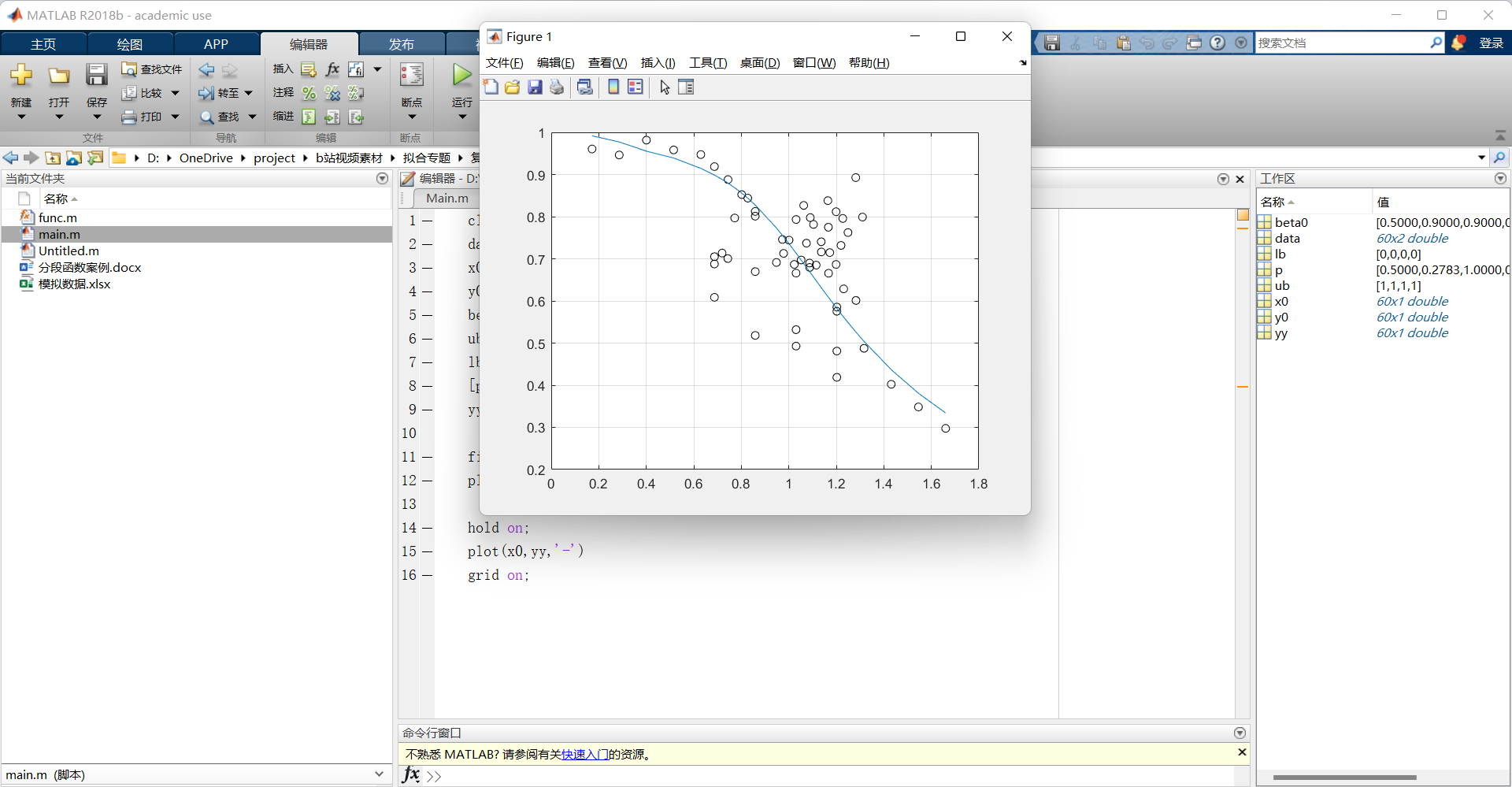
Matlab实现分段函数拟合（分段点未知）| 源码分享 | 视频教程 | 三种分段函数拟合方法

专栏导读作者简介：工学博士，高级工程师，专注于工业软件算法研究本文已收录于专栏：《复杂函数拟合案例分享》本专栏旨在提供 1.以案例的形式讲解各类复杂函数拟合的程序实现方法，并提供所有案例完整源码；2.复杂函数包含：分段函数、积分函数、常/偏微分函数、隐函数、方程组、级数函数、多参数函数；3.拟合工具是Matlab种的lsqcurvefit， nlinfit，神经网络，ga遗传算法，MultiS

#未知编码的字符串.startsWith(#)为什么会是false UTF-8 BOM编码的坑

"#未知编码的字符串".startsWith("#")为什么会是false? 我都这么命名标题了，那么问题很显然，编码不统一导致。发现这个问题的背景：我在获取别人的t配置信息（txt文件）时，如果遇到以“#”开头，则说明是注释信息。但是我在用.startsWith("#")去判断时，居然出现这样的情况：一开始以为是“#”需要转义，尝试转义却途劳；然后

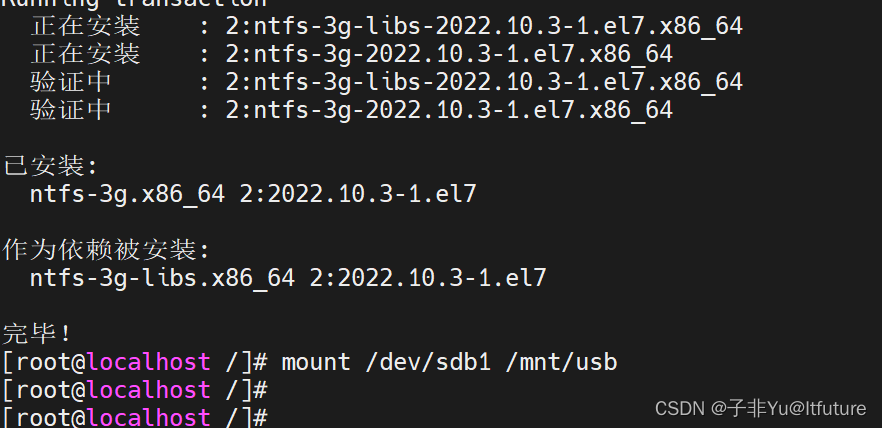
Linux提示：mount: 未知的文件系统类型“ntfs”

mount: 未知的文件系统类型“ntfs” 在Linux系统中，如果遇到“mount: 未知的文件系统类型‘ntfs’”的错误，这通常意味着您的系统没有安装支持NTFS文件系统的软件。为了挂载NTFS文件系统，您需要安装ntfs-3g软件包。以下是如何在不同Linux发行版上安装ntfs-3g并解决这个问题的步骤：安装ntfs-3g：对于基于Debian的系统（如Ubuntu），使用

MFC vc++严重性代码说明项目文件行禁止显示状态错误 C3646 “m_SockClient”: 未知重写说明符

https://www.cnblogs.com/txwtech/p/11074283.html MFC vc++严重性代码说明项目文件行禁止显示状态错误 C3646 “m_SockClient”: 未知重写说明符严重性代码说明项目文件行禁止显示状态错误 C3646 “m_SockClient”: 未知重写说明符 MFC_TCP_CSocket_Client c:\

跨越未知，拥抱挑战——新征程

在浩瀚的IT领域里，每一位开发工程师都如同一位探险家，不断地探索、挑战和成长。作为一名新入职的Java开发工程师，我面临着全新的技术栈和业务领域，这是一次跨越未知的征程，也是一次自我提升的机会。新入职初入公司，我首先感受到的是技术的巨大差异。过去，我熟悉的是一套相对固定的技术体系和开发流程，而在这里，我需要面对的是全新的框架、工具和开发模式。这种变化让我感到既兴奋又紧张。兴奋的是，我能够接

斯坦福HAI年度报告增加AI4S；美阿贡国家实验室与日本最大综合研究机构建立合作；催化剂加获得深势科技未知金额投资

AI for Science 企业动态速览—— Cota Healthcare 与赛诺菲达成合作腾讯牵头共建医疗影像国家新一代人工智能开放创新平台催化剂加获得深势科技未知金额投资 TetraScience 与 Google Cloud 合作促进科学人工智能创新美国阿贡国家实验室和日本理化学研究所签署谅解备忘录《2024 年人工智能指数报告》增加 AI4S 相关内容美年健康

[运动规划算法]空中机器人在未知环境中的快速自主探索

文章目录前言一、快速自主飞行中的重规划方法1.基于梯度的轨迹优化方法2.Perception-aware replanning 二、快速自主探索中的层级规划方法1.增量式边界检测和聚类2.全局行程规划3.局部视点细化4.局部轨迹生成三、完整自主飞行系统四、总结1.现存的问题2.未来的研究方向前言来自香港科技大学周博宇的线上Talk分享https://www.tech

未知个数一维数组：申请资源、初始化、访问、释放资源

示例： /*** @brief how about array-unknown-count? show you here.* @author wen`xuanpei* @email 15873152445@163.com(query for any question here)*/#define _CRT_SECURE_NO_WARNINGS//support c-library in

bp神经网络拟合函数未知参数【源码+视频教程】

专栏导读作者简介：工学博士，高级工程师，专注于工业软件算法研究本文已收录于专栏：《复杂函数拟合案例分享》本专栏旨在提供 1.以案例的形式讲解各类复杂函数拟合的程序实现方法，并提供所有案例完整源码；2.复杂函数包含：分段函数、积分函数、常/偏微分函数、隐函数、方程组、级数函数、多参数函数；3.拟合工具是Matlab种的lsqcurvefit， nlinfit，神经网络，ga遗传算法，MultiS