ThreeJS 坐标系（旋转跳跃，永不停歇）

ThreeJS 坐标系（旋转跳跃，永不停歇）

本文主要介绍 threejs 中3D坐标系的内容，内容包含世界坐标系（world coordinate system）与局部坐标系（local coordinate system）之间的区别与关系；3D 对象之间建立父子关系时平移、旋转、缩放转换；简单介绍底层数学层面如何支持 3D 对象进行平移、旋转、缩放。

3D 坐标系

3D 空间通常采用3个坐标轴来进行表示分别是x、y、z。 这三个坐标轴有两种布置方式分别是左手坐标系和右手坐标系（它们是以坐标轴的朝向来命名的）。

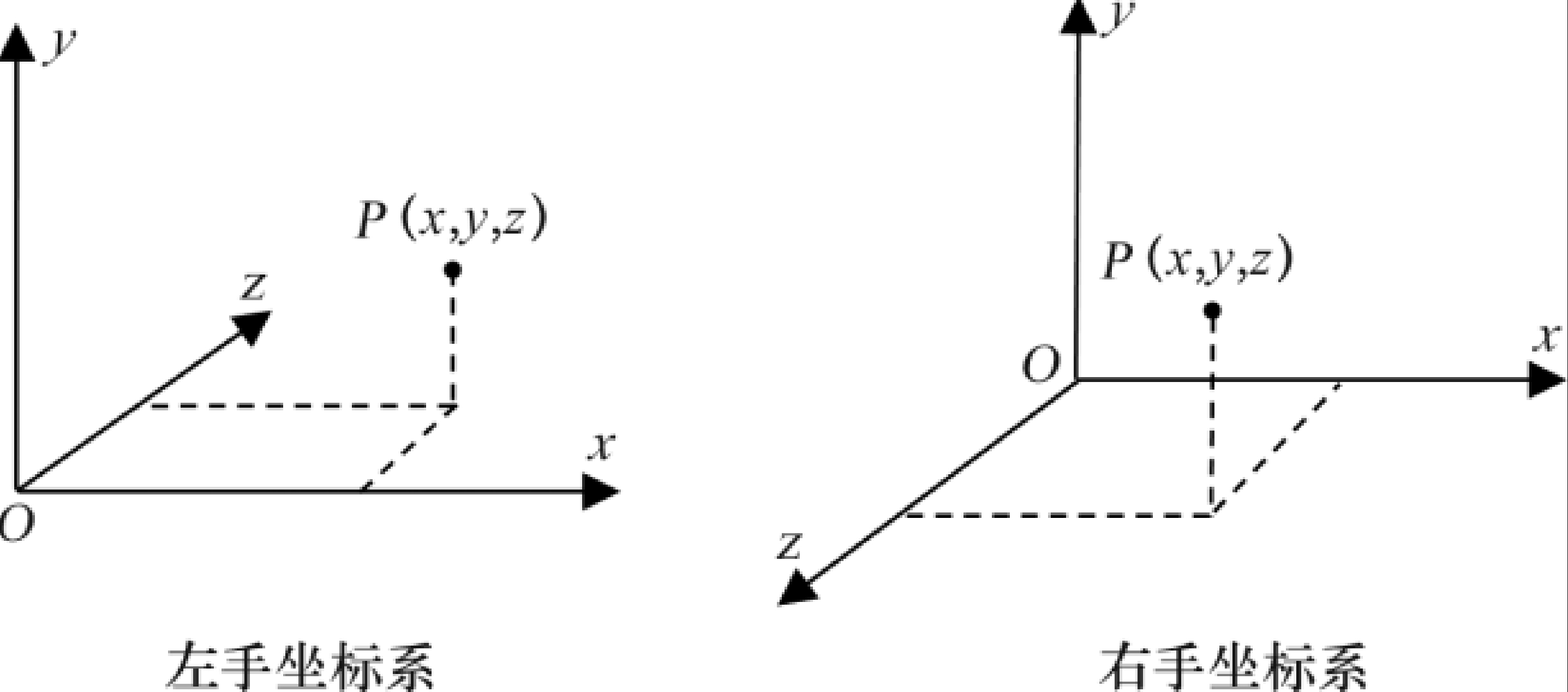
openGL 采用的是右手坐标系，WebGL 是openGL的JS版本也是右手坐标系。ThreeJS 依然采用的右手坐标系。而 Direct3D 使用的坐标系则是左手坐标系。右手坐标系和 3D 笛卡尔坐标系是一样的。

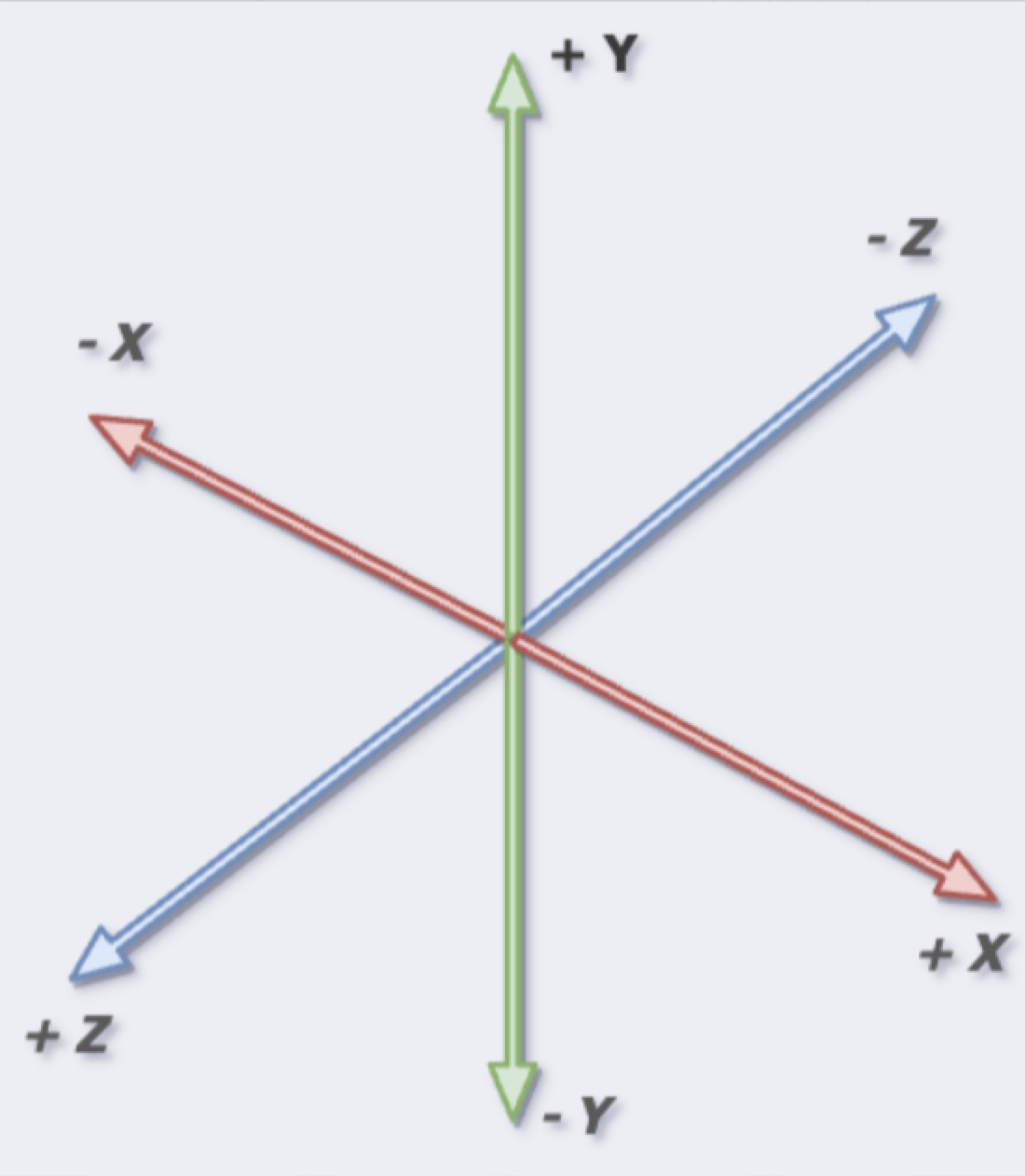  3D笛卡尔坐标系

ThreeJS 中有几个 2D、3D 坐标系，本文主要介绍最重要的世界坐标系（world coordinate system）、局部坐标系（local coordinate system）两个。剩余的会在该系列的其他文章中进行介绍（屏幕坐标系、相机坐标系等）。

世界坐标系&局部坐标系

上一篇文章【加个传送门: ThreeJS 入门创建第一个3D对象】中有介绍 THREE.Scene 创建 scene 场景，创建后的 scene 就是个小宇宙，这个小宇宙就是世界空间，世界空间中的坐标系称为世界坐标系。

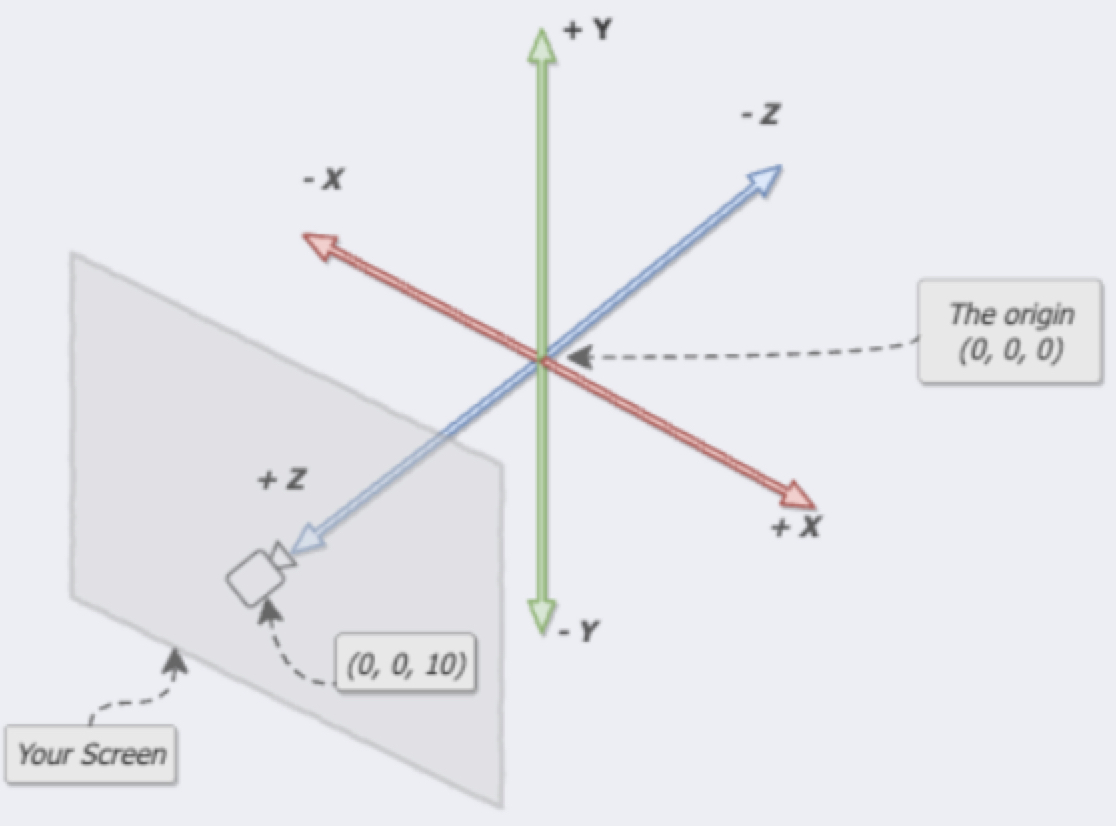        scene 定义世界坐标系

当我们往 scene 中添加 3D 对象并进行平移、旋转、缩放等操作时，该对象就是相对于 scene的世界坐标系进行移动。

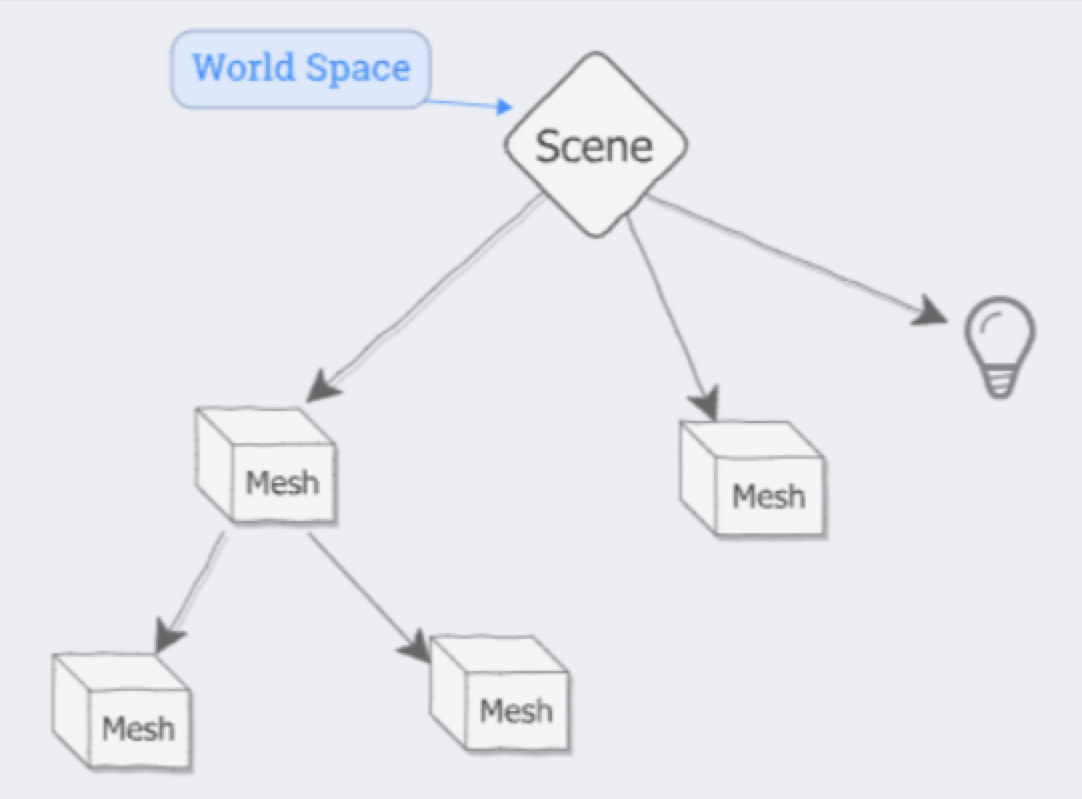scene 中的 Mesh

通常使用修改 position 值来实现平移；通过修改 rotation 值来实现旋转；使用设置 scale 来实现缩放。

// 创建场景
const scene = new THREE.Scene();

// 新建一个 mesh
const geometry = new THREE.BoxGeometry(1,1,1);
const material = new THREE.MeshBasicMaterial({color: 0x00000ff});
const meshA = new THREE.Mesh(geometry, material);

// 将 mesh 添加到scene 中
scene.add(meshA);

// 将 meshA 延x轴方向移动5m，这里的x轴是相对于世界坐标系而言
meshA.position.x = 5;

在 ThreeJS 中长度单位默认是米（meter）, 通过设置 position 的值就是来进行平移。scene 中可添加Mesh对象、光照对象、相机对象等。 Mesh 内部还涉及到局部空间和局部坐标系（local coordinate system） ，Mesh 上还可以添加 Mesh（将一个Mesh作为另一个Mesh的children， child Mesh 位置变换就会相对于 parent Mesh 的局部坐标系进行变换计算）。再回过头来看看这张图：

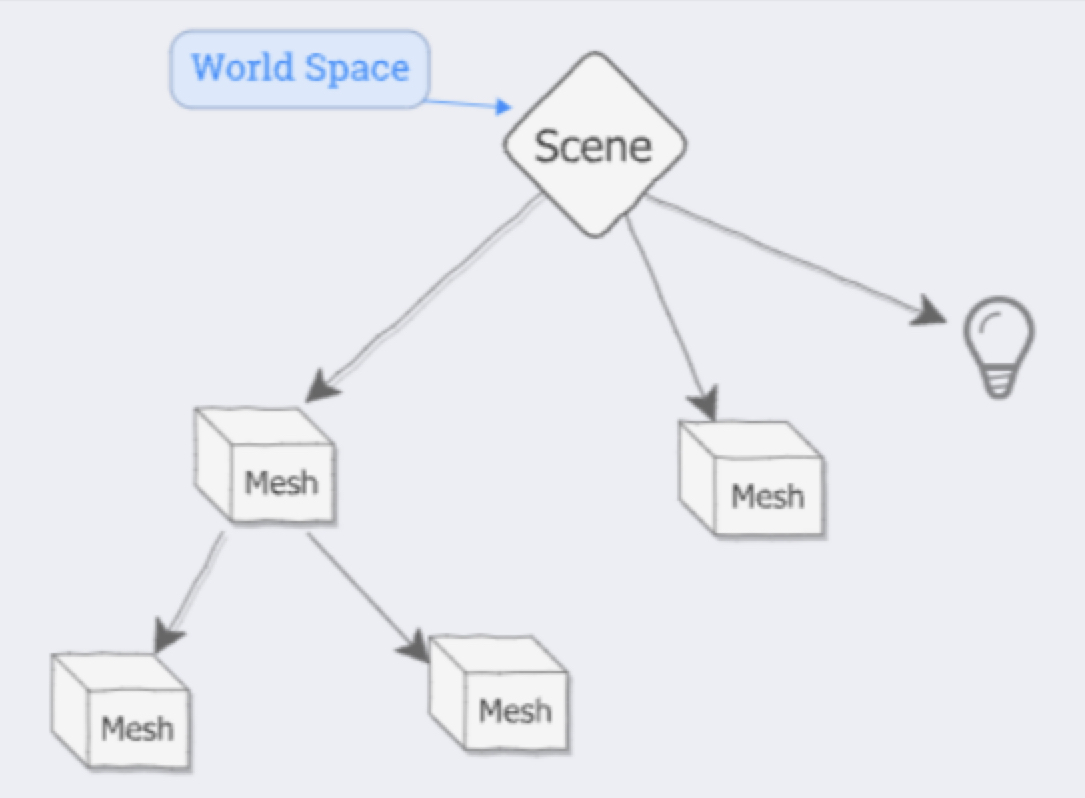scene 中的 Mesh

我们使用一个简单的 demo 来介绍这中间的区别，创建两个 Mesh。meshA 棕红色222的立方体， meshB 红色的111的立方体。 第一次验证：两个 Mesh 平级添加到scene中 其中 meshA延X轴移动1m，meshB延Y轴移动1m。 第二次验证：将meshB添加到meshA上，meshB 作为 meshA 的 children。执行同样的移动操作

开始试验前，我们创建一个scene的全局辅助坐标系。

// AxesHelper：辅助观察的坐标系
const axesHelper = new THREE.AxesHelper(200)
scene.add(axesHelper)

红色X轴正方向，绿色Y轴正方向。效果如下：

实验一：两个mesh平级，执行移动命令

// 新建一个 meshA 蓝色的 2*2*2 的立方体
const geometry = new THREE.BoxGeometry(2, 2, 2)
const material = new THREE.MeshMatcapMaterial({
  color: 0x862d2d,
  opacity: 0.2,
})
const meshA = new THREE.Mesh(geometry, material)
meshA.position.set(1.1, 1.1, 0)

// 新建一个 meshB 红色 1*1*1 的立方体
const geometryB = new THREE.BoxGeometry(1, 1, 1)
const materialB = new THREE.MeshMatcapMaterial({ color: 0xff0000 })
const meshB = new THREE.Mesh(geometryB, materialB)

meshA.add(meshB)

// 为了将两个立方体位置展示出来，需要将 meshB 向z轴（相机方向靠近一点）
meshB.position.z = 1

// 将 mesh 添加到scene 中
scene.add(meshA)


// 新建一个 meshA 蓝色的 2*2*2 的立方体
const geometry = new THREE.BoxGeometry(2, 2, 2)
const material = new THREE.MeshMatcapMaterial({
  color: 0x862d2d,
  opacity: 0.2,
})
const meshA = new THREE.Mesh(geometry, material)

// 新建一个 meshB 红色 1*1*1 的立方体
const geometryB = new THREE.BoxGeometry(1, 1, 1)
const materialB = new THREE.MeshMatcapMaterial({ color: 0xff0000 })
const meshB = new THREE.Mesh(geometryB, materialB)

// 为了将两个立方体位置展示出来，需要将 meshB 向z轴（相机方向靠近一点）
meshB.position.z = 1

// 将 mesh 添加到scene 中
scene.add(meshA)
scene.add(meshB)

// meshA 往x轴移动2m
meshA.position.x = 2

// meshB  往y轴移动2m
meshB.position.y = 2

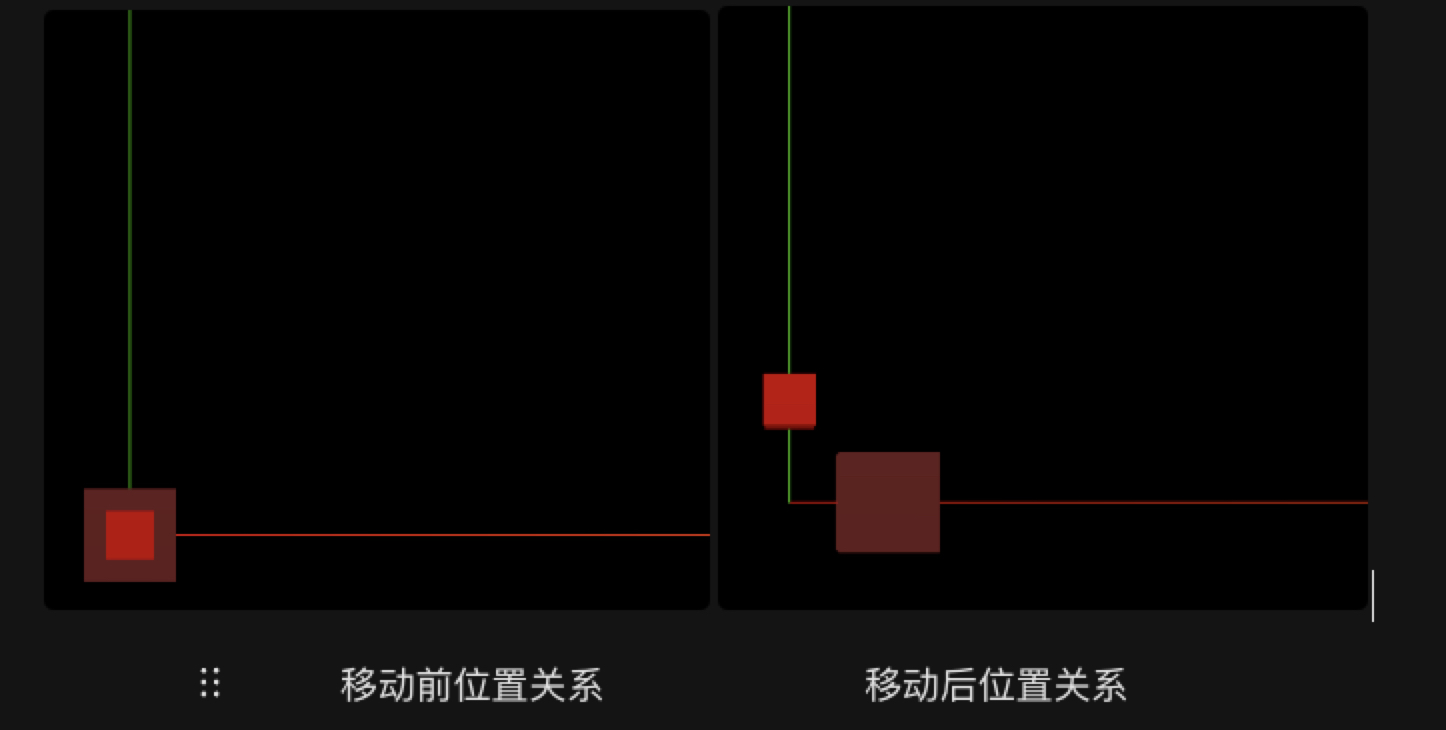
此时两个立方体都是相对于世界坐标系进行的移动，互相之间没有影响。

实验二：将meshB添加到meshA上，meshB 作为 meshA 的 children。执行同样的移动命令。

// 新建一个 meshA 蓝色的 2*2*2 的立方体
const geometry = new THREE.BoxGeometry(2, 2, 2)
const material = new THREE.MeshMatcapMaterial({
  color: 0x862d2d,
  opacity: 0.2,
})
const meshA = new THREE.Mesh(geometry, material)
meshA.position.set(1.1, 1.1, 0)

// 新建一个 meshB 红色 1*1*1 的立方体
const geometryB = new THREE.BoxGeometry(1, 1, 1)
const materialB = new THREE.MeshMatcapMaterial({ color: 0xff0000 })
const meshB = new THREE.Mesh(geometryB, materialB)

meshA.add(meshB)

// 为了将两个立方体位置展示出来，需要将 meshB 向z轴（相机方向靠近一点）
meshB.position.z = 1

// 将 mesh 添加到scene 中
scene.add(meshA)


// 新建一个 meshA 蓝色的 2*2*2 的立方体
const geometry = new THREE.BoxGeometry(2, 2, 2)
const material = new THREE.MeshMatcapMaterial({
  color: 0x862d2d,
  opacity: 0.2,
})
const meshA = new THREE.Mesh(geometry, material)

// 新建一个 meshB 红色 1*1*1 的立方体
const geometryB = new THREE.BoxGeometry(1, 1, 1)
const materialB = new THREE.MeshMatcapMaterial({ color: 0xff0000 })
const meshB = new THREE.Mesh(geometryB, materialB)

// 为了将两个立方体位置展示出来，需要将 meshB 向z轴（相机方向靠近一点）
meshB.position.z = 1

// 将 mesh 添加到scene 中
scene.add(meshA)
// !!!! 注意代码变更 scene.add(meshB) -> meshA.add(meshB)
meshA.add(meshB)

// meshA 往x轴移动2m
meshA.position.x = 2

// meshB  往y轴移动2m
meshB.position.y = 2

实验二对比实验一只有一行代码变更： scene.add(meshB) -> meshA.add(meshB)

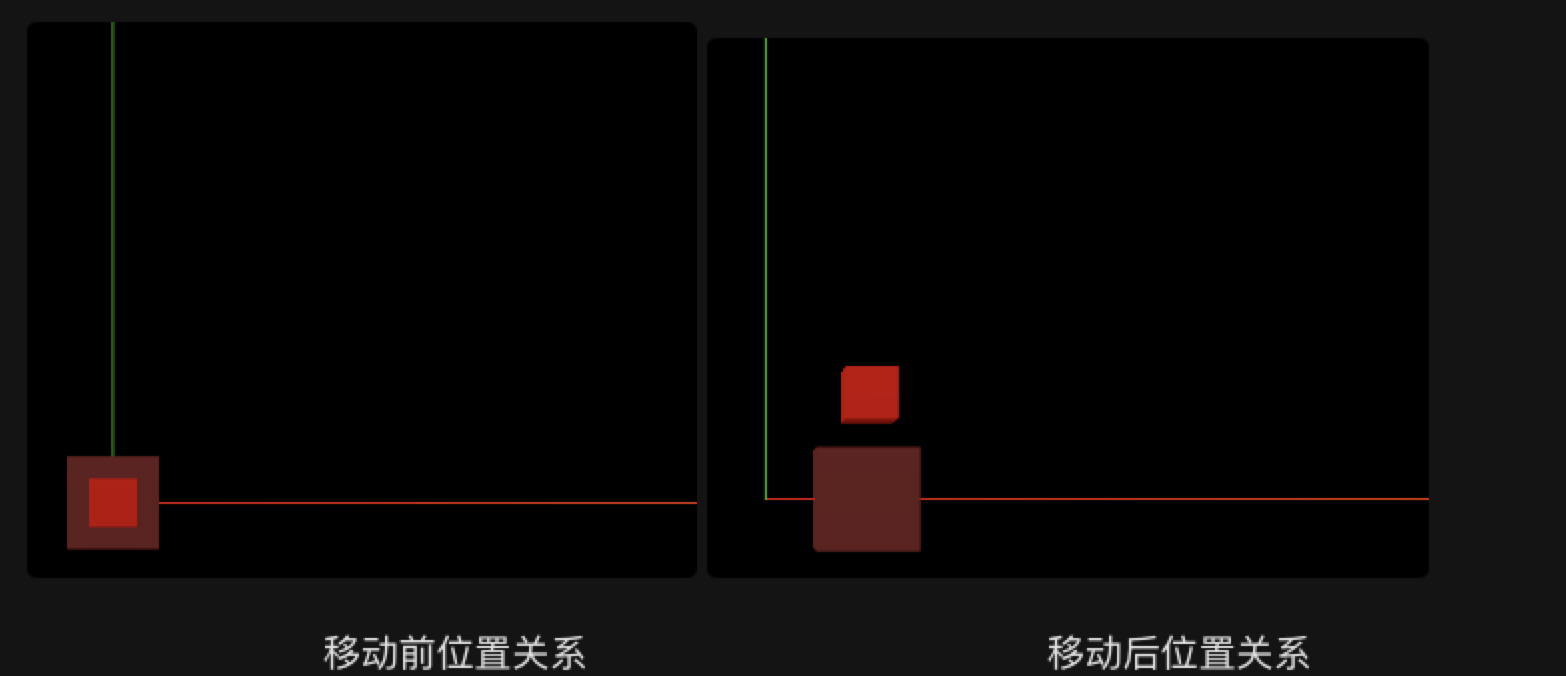
执行了同样的移动命令，但是效果确不一样。原因是：实验一，两个立方体都是相对于世界坐标系进行的移动，彼此之间互不影响（矩阵计算上不会影响）。实验二中 meshA 依然是相对于世界坐标系进行移动，meshB 移动参考的坐标系不再是世界坐标系而是meshA的局部坐标系。meshA 移动的时候已经将它的局部坐标系沿着世界坐标系进行移动了2m。

规律：每当我们变换一个对象时，都是相对于它的父坐标系进行的。

实验二中的关系：scene->meshA->meshB 计算时 meshA移动计算相对于scene的坐标系（这里就是世界坐标系）， meshB 移动计算时相对的坐标系是 meshA的局部坐标系。

每个人都需要自己的房子，不然孩子没地方住。每个 mesh 都有自己的空间，所有的children都将参考parent的坐标系进行变换【移动、旋转、缩放】。

虽然每个 mesh 都有自己的坐标系，但是最后呈现到屏幕上我们看见的还是基于世界坐标系的。

我们介绍了平移操作（修改 position 值来实现），其他两种变换是怎样进行的呢？旋转和缩放操作的单位还是 meter 么？欧拉角、四元数是什么？为什么是三维坐标系最后矩阵计算的时候却是四行四列的矩阵计算呢？欢迎继续跟踪 ThreeJS 系列文章。