残缺棋盘（分治策略--递归）

残缺棋盘（分治策略）

残缺棋盘是指有2^k x 2^k个方格的棋盘中恰好有一个方格是坏的。

在残缺棋盘问题中，我们要用三方块把棋盘填满。要求在铺的过程中三方块不能重叠，不能盖住残缺的方块，并且要铺满其他所有方块。

样例：

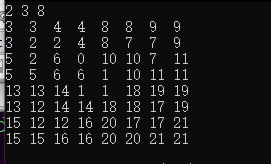
可以采用分治策略的方式（类似于常见的递归的方式），将棋盘划分成四部分。一部分含有残缺块，其他三部分完整。将完整的三部分的位于整个棋盘中间部分的三个方格填充，并将其当作新的残缺块。然后，对四个部分重复上述操做，递归求解。
 

//1.按左上角优先递归
//2.将填充的棋盘块当成新的残缺块进行处理
#include <iostream>
#include<cstdio>
using namespace std;
int board[10000][10000];
int tile=1;
void TileBoard(int topRow,int topColumn,int defectRow,int defectColumn,int Size);
int main()
{
int topRow=0,topColumn=0,defectRow,defectColumn,Size;
//棋盘左上角坐标（topRow，topColumn），残缺块的坐标（defectRow，defectColumn），边长Size
cin>>defectRow>>defectColumn>>Size;
TileBoard(topRow,topColumn,defectRow,defectColumn,Size);
for(int i=0;i<Size;i++){
for(int j=0;j<Size;j++)
printf("%-3d",board[i][j]);
cout<<endl;
}
return 0;
}void TileBoard(int topRow,int topColumn,int defectRow,int defectColumn,int Size){
if(Size==1) return;
int tileToUse=tile++;
int quadrantSize=Size/2;
//残缺块左上角1/4部分 if(defectRow<topRow+quadrantSize&&defectColumn<topColumn+quadrantSize){
TileBoard(topRow,topColumn,defectRow,defectColumn,quadrantSize);
}
else{
board[topRow+quadrantSize-1][topColumn+quadrantSize-1]=tileToUse;
TileBoard(topRow,topColumn,topRow+quadrantSize-1,topColumn+quadrantSize-1,quadrantSize);
}//残缺块右上角1/4部分
if(defectRow<topRow+quadrantSize&&defectColumn>topColumn+quadrantSize-1){
TileBoard(topRow,topColumn+quadrantSize,defectRow,defectColumn,quadrantSize);
}
else{
board[topRow+quadrantSize-1][topColumn+quadrantSize]=tileToUse;
TileBoard(topRow,topColumn+quadrantSize,topRow+quadrantSize-1,topColumn+quadrantSize,quadrantSize);
}//残缺块左下角1/4部分
if(defectRow>topRow+quadrantSize-1&&defectColumn<topColumn+quadrantSize){
TileBoard(topRow+quadrantSize,topColumn,defectRow,defectColumn,quadrantSize);
}
else{
board[topRow+quadrantSize][topColumn+quadrantSize-1]=tileToUse;
TileBoard(topRow+quadrantSize,topColumn,topRow+quadrantSize,topColumn+quadrantSize-1,quadrantSize);
}//残缺块右下角1/4部分
if(defectRow>topRow+quadrantSize-1&&defectColumn>topColumn+quadrantSize-1){
TileBoard(topRow+quadrantSize,topColumn+quadrantSize,defectRow,defectColumn,quadrantSize);
}
else{
board[topRow+quadrantSize][topColumn+quadrantSize]=tileToUse;
TileBoard(topRow+quadrantSize,topColumn+quadrantSize,topRow+quadrantSize,topColumn+quadrantSize,quadrantSize);
}
}