#智能小车项目（六）麦克纳姆轮x型运动学分析

本文主要是介绍#智能小车项目（六）麦克纳姆轮x型运动学分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

麦伦介绍

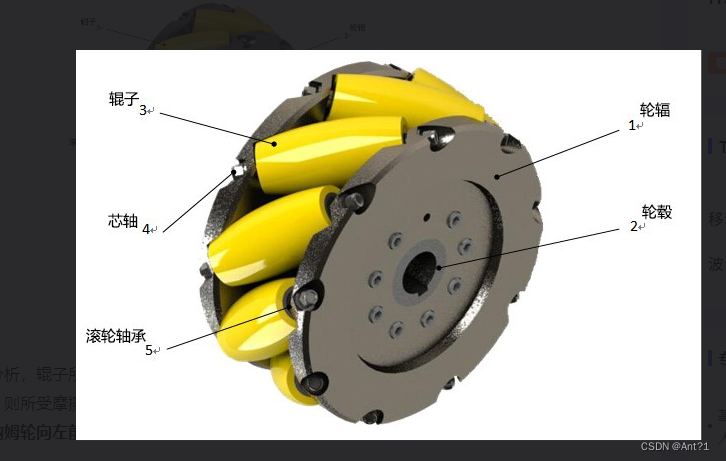
瑞典麦克那姆公司发明的一种全方位移动轮式结构，由基于主体轮辋和一组均匀排布在轮毂周围的回转辊子组成且辊子轴线与轮毂轴线呈一定角度(一般为 45°)，小辊子的母线是等速螺旋线或椭圆弧近似而成，当轮子绕着轮毂轴线转动时，周边各小辊子的外包络线为圆柱面，因此该轮可以连续地向前滚动。

运动分析

（1）轮子逆时针旋转时

选取其中一个辊子做受力分析，辊子所受摩擦力方向与其运动趋势方向相反。当麦克纳姆轮逆时针时，辊子相对于地面有向右前方运动的趋势，则所受摩擦力方向为接触点左后方向。分解此时的辊子运动，则会得到向后以及向左的速度分量，所以说此时麦克纳姆轮向左前方运动。

（2）轮子顺时针旋转时

选取其中一个辊子做受力分析，辊子所受摩擦力方向与其运动趋势方向相反。当麦克纳姆轮顺时针时，辊子相对于地面有向左后方运动的趋势，则所受摩擦力方向为接触点右前方向。分解此时的辊子运动，则会得到向前以及向右的速度分量，所以说此时麦克纳姆轮向右前方运动。
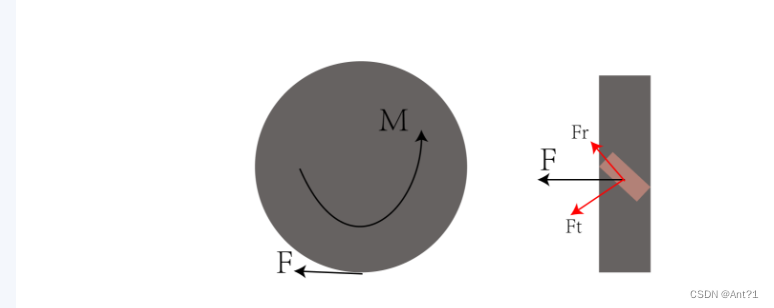
在这里插入图片描述

在这里插入图片描述

当麦轮受电机驱动时，驱动力矩使得绕轮毂轴转动，辊子会与地面产生摩擦力F，其作用力方向与抵消力矩方向一致
将地面摩擦力Ff沿着垂直和平行于辊子轴线方向进行力分解，由于辊子是被动轮，因此会受到垂直于轮毂轴线的分力Ft作用而被动转动，也说明分力Ft是滚动摩擦力，对辊子的磨损较大；沿着轮毂轴线的分力Fr也会迫使辊子运动，是主动运动（辊子被轴线两侧轮毂机械限位），所以分力Fr是静摩擦，滚动摩擦力促使辊子转动，属于无效运动；静摩擦力促使辊子相对地面运动，带动整个麦轮沿着辊子轴线运动。

因此，电机输入轮毂的扭矩，一部分被辊子自转“浪费掉”，另一部分形成静摩擦驱动麦轮整体运动；单个麦轮实际的（受力）运动方向为辊子轴向方向，因此改变辊子轴线和轮毂轴线的夹角，就可以改变麦轮实际的（受力）运动方向。

麦伦布局

在这里插入图片描述
A轮斜优4向上45°

B轮斜左向下45°

在这里插入图片描述
对角成x型

一圈为O型

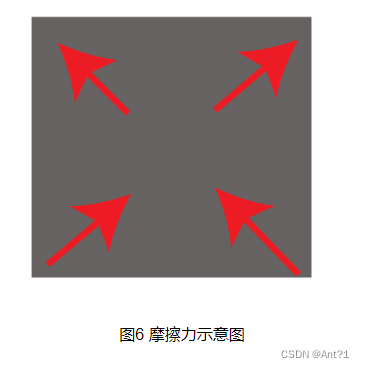
在这里插入图片描述
X-正方形：当主轮在电机转矩的驱动下，主轮转动产生的力矩经摩擦力分解后，辊子分解力一部分垂直于辊子，一部分沿辊子轴线，这两部分摩擦力垂直方向的另辊子空转，浪费力，而沿着辊子轴线的力则可以起到驱动小车运动，因此在X-正方形中，如图6所示，红色箭头表示有效摩擦力，因此在水平方向的摩擦力会被抵消，而向前的摩擦力则驱动整个底盘向前运动。

通过改变主轮旋转方向，可以更改摩擦力的方向。但是，除了可以实现左右前后移动外，当进行旋转运动时，发现无论摩擦力朝向怎么排布，摩擦力始终都会经过会经过同一个点，所以无法保证底盘可以绕中心旋转一定的角度，这很大程度限制了麦轮的活动特性，因此很少使用这种排布方式。

底盘运动分解

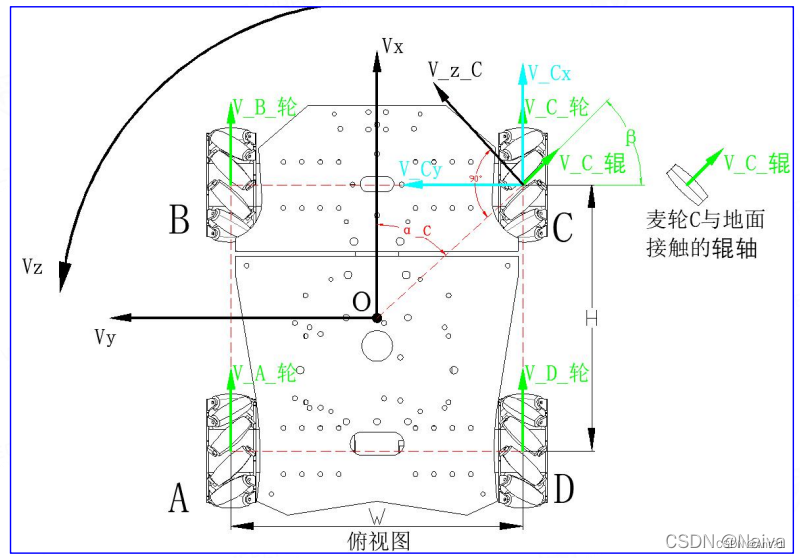
在这里插入图片描述
运动学分析求的就是Vx、Vy、Vz 与 VA轮、VB轮轮、VC轮、VD轮的关系
W：轮距单位：m
H：轴距（前后轮轴心距）单位：m
Vx：小车前后移动速度，前进为正单位：m/s
Vy：小车左右移动速度，前进为右单位：m/s
Vz：小车绕O点旋转速度，逆时针为正，单位：rad/s O点为轮距、轴距中心线的交点
Va轮、Vb轮、Vc轮、Vd轮：麦轮ADBC的速度，由电机转动带动轮毂产生前进为正，单位m/s

Vc辊：麦轮C与地面接触的辊子的线速度，垂直辊轴向前为正单位：m/s。

Vz_C：麦轮C质心绕O点旋转的线速度，正方向垂直于麦轮C质心与O点的连线，偏逆时针方向。
Vc_x：麦轮C质前后移动速度，与小车前后移动速度Vx和小车绕O点旋转速度Vz有关。
Vc_y：麦轮C质左右移动速度，与小车左右移动速度Vy和小车绕O点旋转速度Vz有关。
αc：轮子C质心与O点的连线与前进方向的夹角，αc=arctan(W/H)。
β：轮轴与辊轴之间的夹角为45°。

在这里插入图片描述