51nod-1298 圆与三角形（计算几何超详解）

本文主要是介绍51nod-1298 圆与三角形（计算几何超详解），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目链接：http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1298

给出圆的圆心和半径，以及三角形的三个顶点，问圆同三角形是否相交。相交输出"Yes"，否则输出"No"。（三角形的面积大于0）。

Input第1行：一个数T，表示输入的测试数量(1 <= T <= 10000)，之后每4行用来描述一组测试数据。
4-1：三个数，前两个数为圆心的坐标xc, yc，第3个数为圆的半径R。(-3000 <= xc, yc <= 3000, 1 <= R <= 3000）
4-2：2个数，三角形第1个点的坐标。
4-3：2个数，三角形第2个点的坐标。
4-4：2个数，三角形第3个点的坐标。(-3000 <= xi, yi <= 3000）Output共T行，对于每组输入数据，相交输出"Yes"，否则输出"No"。Sample Input

Sample Output

Yes
No

基础知识回顾：
点到直线距离公式：

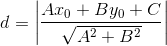
余弦定理：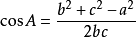

分析：

对于给定的三角形和圆，我们考虑相交的情况：

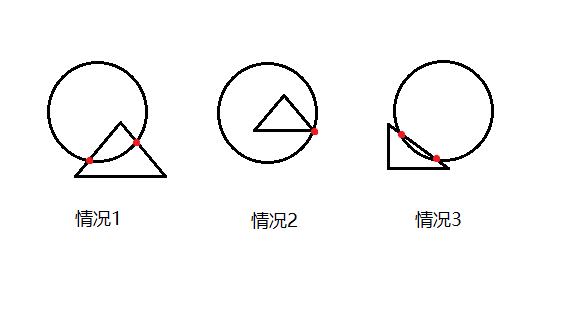
① 三角形有一点在圆内，有一点在圆外。

② 三角形有一点在圆上。

③三角形三点都在圆外，但有一条边与圆相交或相切。

前两种情况比较好写，只需要判断三角形三个端点到圆心的距离与半径的关系即可。

对于第三种情况，我们可以先判断圆心到三角形三条边的距离，如果有一条边到圆心的直线距离小于等于半径，我们进而去判断圆心到这条边所在直线的垂足是否在这条边上。如何去判断呢？

我们可以利用余弦定理，只要圆心与这条边的两个端点所成的角均为锐角（即cosα>0），那么垂足必然落在这条边上。

以下是AC代码：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
struct triangle//用结构体来存三角形三点的坐标
{double x[3],y[3];
};
double x,y,r;
triangle a;
//计算(x1,y1)与(x2,y2)之间的距离的平方 
double point_dist(double x1,double y1,double x2,double y2)
{return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
}
//计算圆心(x,y)到直线Ax+By+C=0的距离的平方 
double line_dist(double A,double B,double C)
{double ans = ( (A*x + B*y + C) * (A*x + B*y + C) ) / (A*A + B*B);return ans > 0 ? ans : -ans;
}
double f(double a,double b,double c)//余弦定理
{return (b + c - a) / (2.0 * sqrt(b * c));
}
int main()
{int i,j,t;cin>>t;while(t--){//Inputscanf("%lf%lf%lf",&x,&y,&r);for(i = 0;i < 3; i++)scanf("%lf%lf",&a.x[i],&a.y[i]);//Solvedouble dis1[3],dis2[3],dis3[3];//dis1存放三角形三点到圆心距离的平方                dis1[0] = point_dist(x,y,a.x[0],a.y[0]);dis1[1] = point_dist(x,y,a.x[1],a.y[1]);dis1[2] = point_dist(x,y,a.x[2],a.y[2]);//dis2存放三角形三条边长的平方 dis2[0] = point_dist(a.x[0],a.y[0],a.x[1],a.y[1]);dis2[1] = point_dist(a.x[1],a.y[1],a.x[2],a.y[2]);dis2[2] = point_dist(a.x[2],a.y[2],a.x[0],a.y[0]);//dis3存放三角形三条边到圆心的直线距离的平方 dis3[0] = line_dist(a.y[0]-a.y[1],a.x[1]-a.x[0],(a.x[0]-a.x[1])*a.y[0]+(a.y[1]-a.y[0])*a.x[0]);dis3[1] = line_dist(a.y[1]-a.y[2],a.x[2]-a.x[1],(a.x[1]-a.x[2])*a.y[1]+(a.y[2]-a.y[1])*a.x[1]);dis3[2] = line_dist(a.y[2]-a.y[0],a.x[0]-a.x[2],(a.x[2]-a.x[0])*a.y[2]+(a.y[0]-a.y[2])*a.x[2]);double t1,t2;t1 = min(dis1[0],min(dis1[1],dis1[2]));//t1为三点到圆心距离最小的那个t2 = max(dis1[0],max(dis1[1],dis1[2]));//t2为三点到圆心距离最大的那个if(t1 <= r*r &&t2 >= r*r)//一点在圆内，一点在圆外或有一点在圆上cout<<"Yes"<<endl;else if(t1 > r*r)//三点都在圆外
        {if(dis3[0] <= r*r)//dis3[0]是由点1和点2连接起来的边到圆心的距离
            {if(f(dis1[0],dis2[0],dis1[1]) > 0 && f(dis1[1],dis2[0],dis1[0]) > 0){cout<<"Yes"<<endl;continue;}}if(dis3[1] <= r*r)//dis3[1]是由点2和点3连接起来的边到圆心的距离
            {if(f(dis1[1],dis2[1],dis1[2]) > 0 && f(dis1[2],dis2[1],dis1[1]) > 0){cout<<"Yes"<<endl;continue;}}if(dis3[2] <= r*r)//dis3[2]是由点1和点2连接起来的边到圆心的距离
            {if(f(dis1[0],dis2[2],dis1[2]) > 0 && f(dis1[2],dis2[2],dis1[0]) > 0){cout<<"Yes"<<endl;continue;}}cout<<"No"<<endl;}elsecout<<"No"<<endl;}return 0;
}