学习笔记|单样本t检验|无统计学意义|规范表达|《小白爱上SPSS》课程：SPSS第四讲

学习目的

SPSS第四讲 | 单样本T检验怎么做？很单纯很简单！

软件版本

IBM SPSS Statistics 26。

原始文档

《小白爱上SPSS》课程
单样本t检验，即考察单个样本的均值与给定常值之间是否存在差异。准确的表达是，检验单个样本所属的总体均值，与给定总体均值之间是否存在差异。如考察运动员心理健康水平与全国成年人心理健康的差异情况，再如某地区居民的身高与基本身高的差异情况，是连续型数据资料中最为常用的方法之一。

一、实战案例

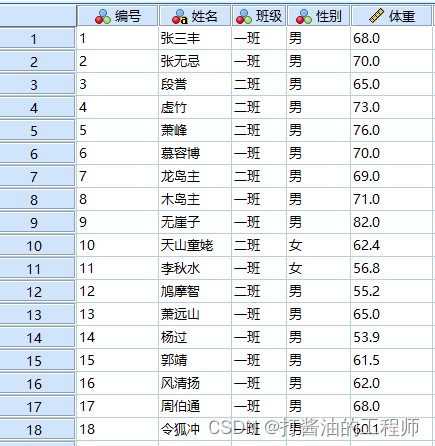
小白共抽取到38名大侠们的体重数据如下，已知全国正常成年人体重平均常值为65kg，标准差为5kg，现需考察江湖中大侠们的体重与全国成年人体重之间是否有差异。
读取数据：

GET FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\第四讲 单样本T检验.sav'.

在这里插入图片描述

二、案例解析

这个案例包括1个变量，38名大侠的体重数据，为连续型变量。

本案例之目的

江湖中的大侠的体重均值与全国成年人体重均值（65kg）有无统计学差异。但江湖中的大侠有很多，不可能穷尽。小白只抽样调查了38名大侠体重，用于代表总体大侠体重，由于存在抽样误差，故需进行统计推断。
三、统计策略
统计分析策略口诀“目的引导设计，变量确定方法”（啥意思？请点击此处一张脑图搞定！统计方法选择）一张图连接。
针对上述案例，扪心自问。
Q1：本案例研究目的是什么？
A：比较差异。比较单个样本均值与给定总体均值（总体平均数μ）之间差异
Q2：本案例属于什么研究设计？
A：属于观察性研究
Q3：有几个变量？
A：只有一个变量
Q4：变量类型是什么？
A：连续型变量
Q5：连续型变量服从正态分布么？
A：需要检验
Q6：可采用何种统计方法？
A：如果服从正态分布（或者近似正态分布），则采用单样本T检验，若是严重偏态分别，则采用秩和检验。
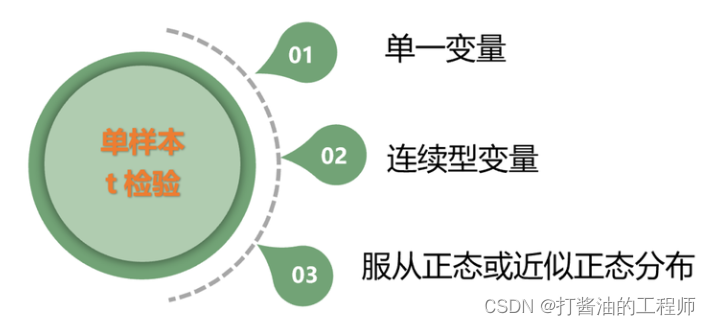
概括而言，如果数据满足以下条件，则采用单样本T检验。
在这里插入图片描述

四、SPSS操作

1、正态性检验

正态性检验的SPSS操作步骤请点击《第三讲 | 正态分布怎么检验》，这里只呈现检验结果。
直方图绘制：GRAPH /HISTOGRAM(NORMAL)=体重.
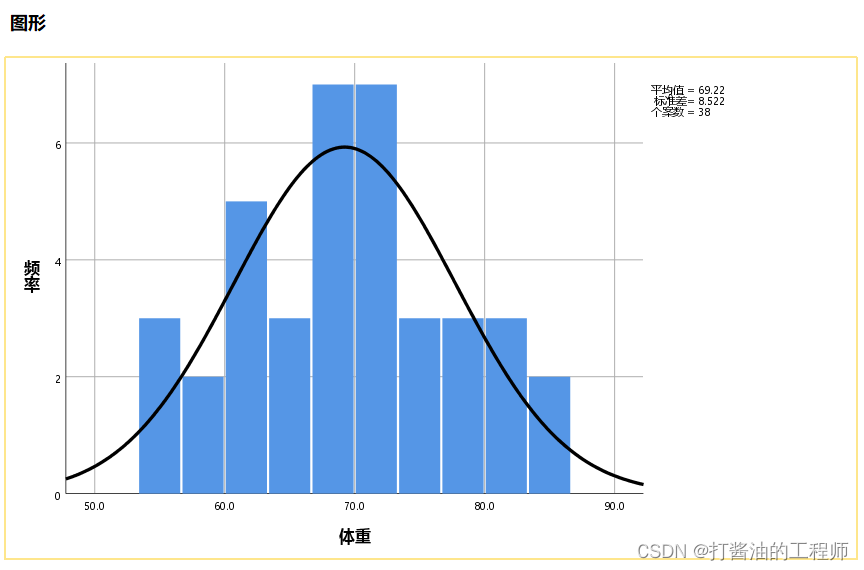
在这里插入图片描述
数据频数分布直方图的形状比较接近于倒扣的“钟形”，左右两边具有对称性，可认为该数据为正态分布数据。
正态检验：

EXAMINE VARIABLES=体重/PLOT BOXPLOT NPPLOT /*若无此行，则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.

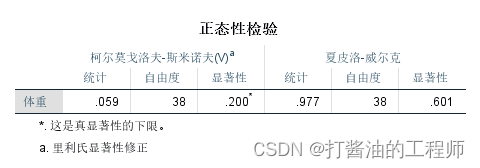
在这里插入图片描述
正态性检验属于非参数检验，原假设为“样本来自的总体与正态分布无显著性差异”，只有P>0.05才能接受原假设，即数据符合正态分布。
经S-W检验，体重数据的P=0.601（P>0.05，接受原假设），没有统计学意义，并结合直方图可认为该组数据符合正态分布。

Tips：无统计学意义

参考什么叫做无统计学意义。
当p值小于0.05时，表示结果在统计学上具有显著性。
这是因为在统计学中，研究者通常会采用显著性水平(Significance Level，α)为0.05作为判断的标准。
换句话说，α=0.05表示研究者可接受出现错误判断(Type I Error，即将无效结果判断为有效)的概率不超过5%。
那么，当p值小于0.05时，说明在显著性水平α=0.05下，观察到的结果仅有不超过5%的概率是由于采样误差或其他随机因素造成的。
因此，p值小于0.05意味着研究结果具有统计学意义，即结果被认为在95%的可信度下，拒绝原假设，表示该测试有统计学上的显著性。
简言之，p<0.05表示有小于5%的概率是观察到假阳性结果，因此我们有足够的证据支持研究结果的统计学意义。这就是p值在统计推断中被广泛应用的原因。

2、t检验结果

Step1：打开SPSS，依次点击“分析——比较平均值——单样本T检验”。
在这里插入图片描述
Step2：出现如下“单变量T检验”窗口。将需要进行T检验的变量“体重”选入右侧“检验变量”框中，并输入检验值“65”。
Step3：点击“确定”。得到“单样本统计”表和“单样本检验”表。
命令行：

T-TEST /TESTVAL=65 /MISSING=ANALYSIS /VARIABLES=体重 /CRITERIA=CI(.95).

五、结果解读

t检验统计分析有两张表，一张为“但样本统计”，另外一张“单样本检验”。
第一张表“单样本统计”分别提供体重数据的样本数（n）、平均值（mean）、标准差（SD）、标准误（SE）。
在这里插入图片描述
第二张表“单样本”给于了t检验的结果。

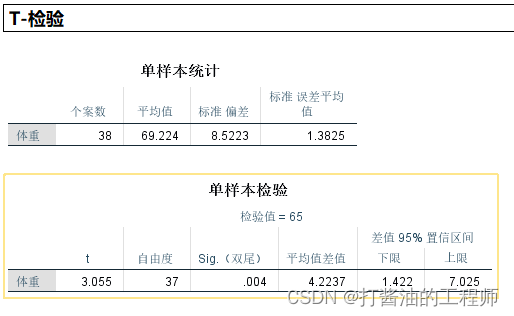
本题中t=3.055，df=37, P(Sig.双尾)=0.004(差异具有统计学意义，说明两总体之间有显著性差异)。同时还给出了平均值差值为4.2237，该差值=大侠体重均值（69.2237）减去全国体重均值（65）。
最后是差值95置信区间（95% CI）上下限为1.422～7.025。
注意：差值95%CI不包括0，说明两总体之间有显著性差异。本例中95%下限为1.422，上限为7.025，没有包括0，所以差异具有统计学意义。

六、规范报告

规范报告有多种方式，本公众号只提供一种方式供参考。

1、规范表格

表大侠与全国成人的体重差异比较结果
在这里插入图片描述

2、规范文字

经S-W检验以及直方图结果显示，数据服从正态分布，故采用单样本T检验。T检验结果显示，大侠的体重显著性高于全国成年人的体重，t=3.06，p=0.004, 95%CI为（1.42～7.03）。

注意

1、虽然有些论文没有报告t、p，只是用*标识显著性，本公众号建议初学者应报告t、p值，以更深刻地理解其含义；
2、现在越来越多的文章需要提供差值的的95%CI, 所以建议今后统计分析时报告差值的95%CI。
3、单样本t检验之前，一定要进行正态性检验，并简要报告正态性检验结果。

划重点

1、单样本t检验一般用于观察性研究，比较单个样本的均值与给定常值之间是否存在差异。
2、单样本t检验的统计策略：单一变量、连续型变量和数据服从正态分布。
3、如果数据服从正态（或近似正态）分布，采用单样本t检验，否则采用秩和检验。
4、建议规范报告t值、p值和差值的95%CI，以及简要报告正态性检验结果。