本文主要是介绍Globally Optimal Toon Tracking,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最近看了师公的一篇文章,果然偶尔看看传统算法的文章,才能对问题的本质有深刻的理解,特此记录,敬畏前人。
该任务的可视化例子如下:
 |  |
|---|
👉原项目地址
1. Optical Flow 不能用于赛璐璐(cel)动画的原因
1️⃣ 不能保证动画的内容(运动)是物理上正确的;
2️⃣ 对象运动更剧烈(Choppy & Vigorous);
3️⃣ 动画对象缺乏充足的纹理。
2. 任务难点
1️⃣ 存在多个外形(Appearance)相似的区域(Region);
2️⃣ 某个 Region 在中途被遮挡(全遮挡与半遮挡);
3️⃣ 某个 Region 可能在某一帧中被分为多个 Regions。
3. 关键思路
1️⃣ 不仅考虑 Region 的 Appearance 信息,而且考虑其运动(Motion)信息;
2️⃣ 同时考虑所有区域的对应关系和他们的完整运动轨迹;而不是简单地追踪相邻帧之间的区域。(意思就是讲整个序列所有帧的所有 Regions 同时考虑);
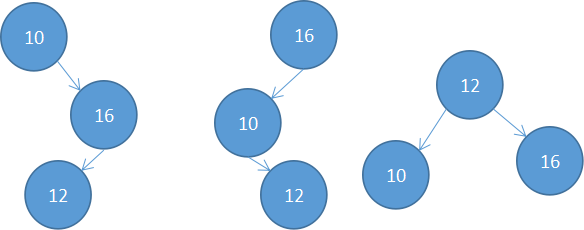
3️⃣ 对所有的 Regions 建立一个无环连通图,👇给个例子揣摩一下怎么构造的

** 无环 是因为根据时序推进去构造连接关系的,以上图为例子:
考虑 F 1 F_1 F1,有 a a a, b b b,其他帧有 c c c, d d d, e e e,则必须有: a ∼ c a\sim c a∼c, a ∼ d a\sim d a∼d, a ∼ e a\sim e a∼e, 与 b ∼ c b\sim c b∼c, b ∼ d b\sim d b∼d, b ∼ e b \sim e b∼e;
考虑 F 2 F_2 F2,有 c c c, 剩下帧中还有 d d d, e e e, 则必须有: c ∼ d c\sim d c∼d, c ∼ e c\sim e c∼e;
考虑 F 3 F_3 F3,有 d d d, e e e,剩下没有多余的帧了。
这注定了未来的图中有 8 个节点(除了起止节点 S S S 和 T T T 外)。
- p.s. 本文定义流图的每个节点是两个区域 a a a 和 b b b 匹配 n a , b n_{a,b} na,b,流经它的路径的代价是两个区域的外观匹配程度(Appearance Term);
- p.s. 图的 edge 表示从跨帧,包含该路径的代价是跨帧的损耗(Motion Term);
于是本文就将相邻帧间的区域匹配问题和统一区域的时序追踪问题转换为:求解所构造的网络流图中的若干短路径的问题(Network Flow Graph Problem)。
- p.s. 至于要求解多少条路径,则是不断迭代、从剩余路径中选择最短的路径,知道整个时序的所有区域都至少被一条路径经过。
找到的这些路径具有以下特点:
- 每一条路径上,如上图橙色路径是 S − [ n b , c ] − [ n c , d ] − T S-[n_{b,c}]-[n_{c,d}]-T S−[nb,c]−[nc,d]−T,说明这些区域是属于同一个区域,并且应该被追踪: b − c − d b-c-d b−c−d;
- 路径上的某个节点对应的两个 Regions 并不在相邻的两帧上时,说明在这中间的几帧中,该 Region 被完全遮挡了;
- 如果有多条路径经过包含的节点中关联到同一个 Region,说明这个节点在时序前后被切分为(Split)或者重新组成(Merge)。
4. 主要方法
下面首先讲解描述 Region 的外观与运动的两个描述器;然后讲一下描述网络流图的节点与路径代价的计算。
4.1 Appearance Term: i.e. Color & Shape Similarity
用颜色和形状来表示。
- 颜色差别用的是区域内的颜色直方图之间的 L 2 L2 L2 距离,即:
C ( a , b ) = ∥ o ( a ) − o ( b ) ∥ 2 \mathcal C(a,b)=\|o(a)-o(b)\|_2 C(a,b)=∥o(a)−o(b)∥2其中的 o ( a ) , o ( b ) o(a), o(b) o(a),o(b) 是颜色直方图(文中取 24 24 24 个 bin)。- 形状使用 IDSC 描述器,即:Inner-distance Shape Context。
1️⃣ 给定两个区域 a a a 和 b b b,抽取他的轮廓点得到 { p 1 a , p 2 a , . . . } \{p_1^a,p_2^a,...\} {p1a,p2a,...} 和 { p 2 b , p 2 b , . . . } \{p_2^b, p_2^b,...\} {p2b,p2b,...},
2️⃣ 对每个点得到他们的形状上下文直方图(Shape context histogram)(😶,这玩意就不知道是个啥)
3️⃣ 计算局部形状不一致程度:(这里“局部”是指两个轮廓点之间)
s ( p i a , p j b ) = 1 2 ∑ k ( h i a ( k ) − h j b ( k ) ) 2 h i a ( k ) + h j b ( k ) s(p_i^a,p_j^b)={1\over 2}\sum_k{{(h_i^a(k)-h_j^b(k))^2}\over{h_i^a(k)+h_j^b(k)}} s(pia,pjb)=21k∑hia(k)+hjb(k)(hia(k)−hjb(k))2
4️⃣ 计算全局形状不一致性:(这里“全局”是指两个区域之间)
首先要对这些轮廓点做配对,两个区域的轮廓点数不一定相同,怎么得到这个匹配 Π a , b \Pi_{a,b} Πa,b 呢?——😶作者说使用的是动态规划,具体没细说。
然后就可以把配对的点的局部形状不一致程度累加起来,即:
S ( a , b ) = ∑ { p i a , p j b } ∈ Π a , b s ( p i a , p j b ) \mathcal S(a,b)=\sum_{\{p_i^a,p_j^b\}\in\Pi_{a,b}}{s(p_i^a,p_j^b)} S(a,b)={pia,pjb}∈Πa,b∑s(pia,pjb)
4.2 Motion Term
文中假设各个区域做的运动是近乎刚性的,且仅考虑旋转和平移(甚至没有考虑缩放,这是本文的一个弱点之一)。
对于两个区域,使用迭代优化的方式来求解从 a a a 到 b b b 的最佳变换测参数,这里的“距离/代价”使用的是上面的形状不一致性来表示,因此有:
{ R a , b , t a , b } = arg min R , t ∑ { p i a , p j b } ∈ Π a , b ∥ R ⋅ p i a + t − p j b ∥ 2 \{\mathbf{R}_{a,b},\mathbf{t}_{a,b}\}=\argmin_{\mathbf{R},\mathbf{t}}\sum_{\{p_i^a,p_j^b\}\in\Pi_{a,b}}{\|\mathbf{R}·p_i^a+\mathbf{t}-p_j^b\|_2} {Ra,b,ta,b}=R,targmin{pia,pjb}∈Πa,b∑∥R⋅pia+t−pjb∥2
4.3 节点的代价
D ( n a , b ) = ( C ( a , b ) + λ 1 S ( a , b ) + λ 2 M ( a , b ) ) ⋅ G ( v − u ) \mathcal D(n_{a,b})=(\mathcal C(a,b)+\lambda_1\mathcal S(a,b)+\lambda_2\mathcal M(a,b))·G(v-u) D(na,b)=(C(a,b)+λ1S(a,b)+λ2M(a,b))⋅G(v−u)
其中, G ( v − u ) = α v − u G(v-u)=\alpha^{v-u} G(v−u)=αv−u 是对时间跨度的惩罚,先验告诉我们,通常一个区域会持续可见,时间跨度越大,这两个区域匹配的可能性更低; M ( a , b ) = ∥ Ω a , b ∥ 1 + ∥ t a , b ∥ 1 \mathcal M(a,b)=\|\Omega_{a,b}\|_1+\|\mathbf{t}_{a,b}\|_1 M(a,b)=∥Ωa,b∥1+∥ta,b∥1 是对运动变换的参数做限制,一般来说,同个区域在两帧之间的变换应该是很小的。另外, λ 1 ∼ [ 0.01 , 0.1 ] \lambda_1\sim[0.01,0.1] λ1∼[0.01,0.1], λ 2 ∼ [ 0.7 , 1.2 ] \lambda_2\sim[0.7,1.2] λ2∼[0.7,1.2], α = 100 \alpha=100 α=100.
4.4 边缘的代价
由于节点表示一个匹配,那么边缘应该度量的是从一个匹配到下一个匹配的变化,结合一个先验知识:
objects in animatios are very likely to move with costant velocities,我们针对运动的平滑性进行建模,就有:
V ( n a , b , n b , c ) = ∥ ∇ Ω a , b , c ∥ 1 + ∥ ∇ t a , b , c ∥ 1 \mathcal V(n_{a,b},n_{b,c})=\|\nabla\Omega_{a,b,c}\|_1+\|\nabla\mathrm{t}_{a,b,c}\|_1 V(na,b,nb,c)=∥∇Ωa,b,c∥1+∥∇ta,b,c∥1
假设 a , b , c a,b,c a,b,c 分别存在于帧 u , v , w u,v,w u,v,w 中,则这两项分别定义为:
∇ Ω a , b , c = ∥ Ω b , c w − v − Ω a , b v − u ∥ 1 \nabla\Omega_{a,b,c}=\|{{\Omega_{b,c}}\over{w-v}}-{{\Omega_{a,b}}\over{v-u}}\|_1 ∇Ωa,b,c=∥w−vΩb,c−v−uΩa,b∥1 ∇ t a , b , c = ∥ t b , c w − v − t a , b v − u ∥ 1 \nabla\mathrm{t}_{a,b,c}=\|{{\mathrm{t}_{b,c}}\over{w-v}}-{{\mathrm{t}_{a,b}}\over{v-u}}\|_1 ∇ta,b,c=∥w−vtb,c−v−uta,b∥1另外定义起止点到第一帧与最后一帧的各个区域的连线的代价:
V ( S , n a , b ) = G ( u − 1 ) \mathcal V(S,n_{a,b})=G(u-1) V(S,na,b)=G(u−1) V ( n a , b , T ) = G ( N − v ) \mathcal V(n_{a,b},T)=G(N-v) V(na,b,T)=G(N−v)
4.5 最终优化目标
∑ J ( ∑ n a , b ∈ J D ( n a , b ) + ∑ ( n a , b , n b , c ) ∈ J λ 3 V ( n a , b , n b , c ) ) \sum_J(\sum_{n_{a,b}\in J}{\mathcal D(n_{a,b})}+{\sum_{(n_{a,b},n_{b,c})\in J}{\lambda_3\mathcal V(n_{a,b},n_{b,c})}}) J∑(na,b∈J∑D(na,b)+(na,b,nb,c)∈J∑λ3V(na,b,nb,c))其中, λ 3 ∼ [ 1.0 , 2.0 ] \lambda_3\sim[1.0,2.0] λ3∼[1.0,2.0].
5. 最后简要罗列一下作者在文中提到的一些缺点
1️⃣ 依赖区域分割的准确性[1],如果分割结果不好,匹配、追踪的精度也不高;
2️⃣ 假定运动变换是刚性的;
3️⃣ 当有很多外观相同且紧挨着的区域在运动的时候也很难处理;
4️⃣ 遮挡的时间不能太长,不然也会“跟丢”。
这篇关于Globally Optimal Toon Tracking的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




![[论文阅读笔记31] Object-Centric Multiple Object Tracking (ICCV2023)](https://img-blog.csdnimg.cn/direct/e45906a3acc34a5e9398ebc675fbd75e.png)