本文主要是介绍IPDAE: Improved Patch-Based Deep Autoencoder for Lossy Point Cloud Geometry Compression,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- IPDAE: Improved Patch-Based Deep Autoencoder for Lossy Point Cloud Geometry Compression
- 采样点的octree编码
- 集成的压缩和训练过程
- 熵编码的可学习上下文模型
- 对抗学习
- 均匀性度量
- 实验结果
IPDAE: Improved Patch-Based Deep Autoencoder for Lossy Point Cloud Geometry Compression
https://arxiv.org/abs/2208.02519v1

这篇文章提出的IPDAE是PDAE的改进模型,包括以下改进:
1) 为了减少采样点的比特消耗,IPDAE使用octree对采样点进行编码。
2) 集成的压缩和训练过程。与PDAE中使用独立分块的训练集来训练自编码器不同,IPDAE每次迭代训练用一个点云的所有分块进行训练,从而利用输入和重建的完整点云计算得到的失真和率损失进行全局优化。
3) 熵编码的可学习上下文模型。IPDAE使用采样点作为上下文信息输入熵模型估计每个分块在瓶颈层的表示中各个元素的概率分布。
4) 对抗学习。IPDAE还包含一个判别器,通过对抗学习的方法进一步训练自编码器,使得重建的点云更加均匀。
此外,这篇论文还提出了一种度量来评估重建点云的均匀性。
采样点的octree编码
图3对比了PDAE和IPDAE的对采样点的传输方式。PDAE直接传输采样点;而IPDAE使用octree对采样点进行编码后再传输,这可以在熵编码期间有效地压缩点云的采样点信息,从而减少比特消耗。
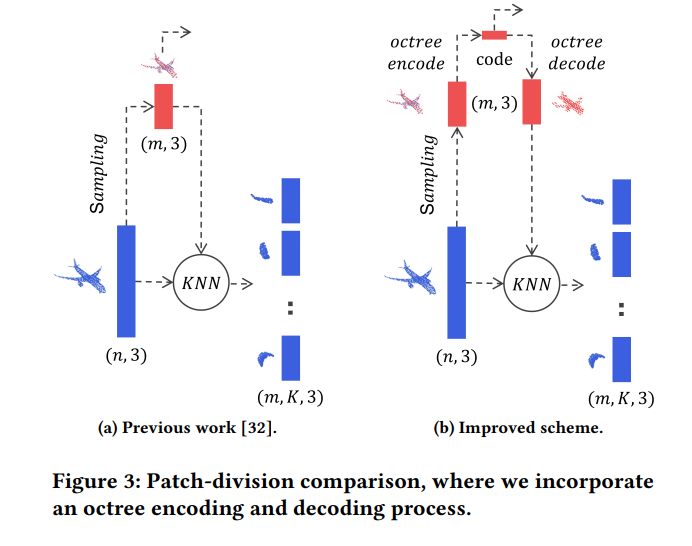
值得注意的是,采样点通过octree编码后,其重建质量和比特率之间的权衡可以通过固定octree的深度或直接将octree编码比特流的比特率设置为某个值来实现。作者使用的是后者。
集成的压缩和训练过程
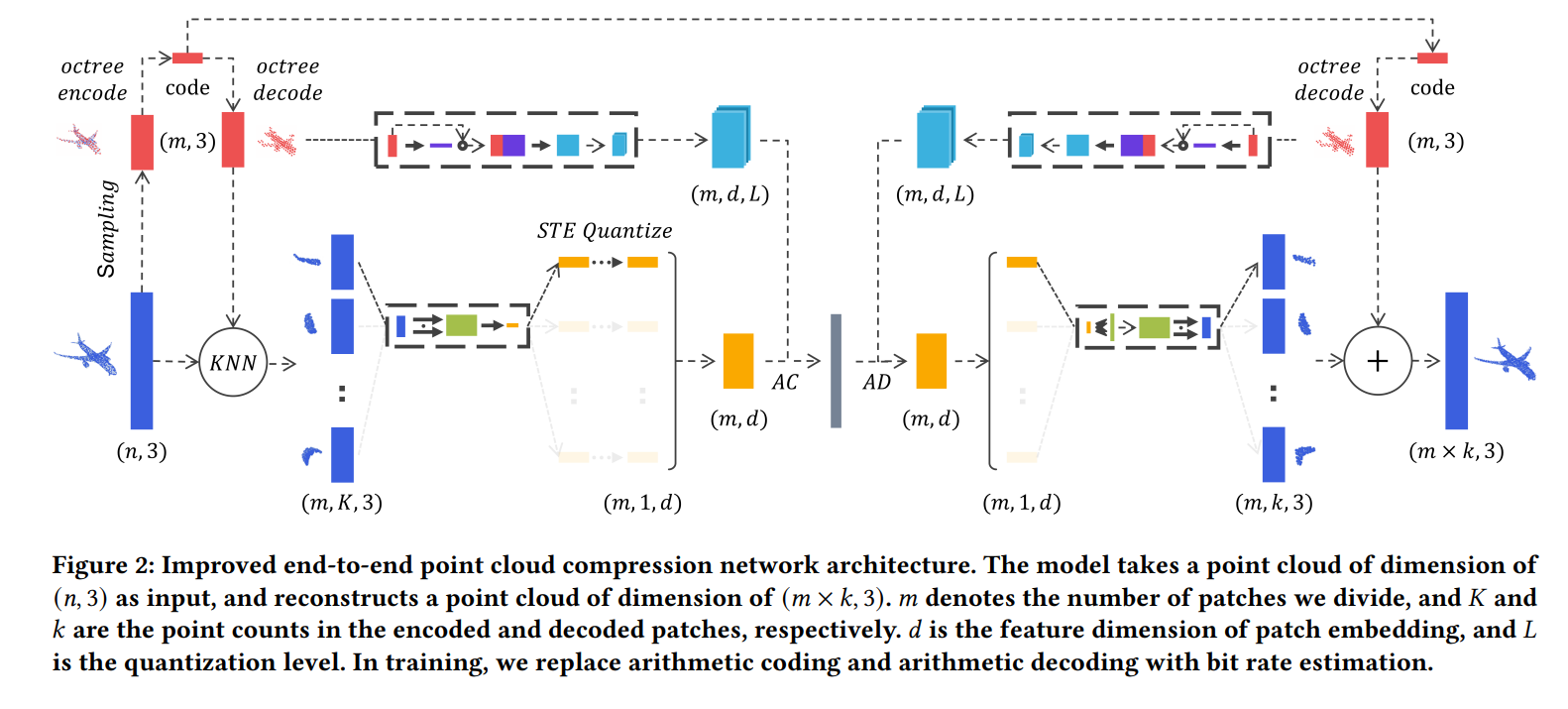
对于 n n n个点的点云 S = { x 1 , x 2 , . . . , x n } S=\{x_1,x_2,...,x_n\} S={x1,x2,...,xn},IPDAE首先通过FPS得到 m m m个采样点 S ′ = { x 1 ′ , x 2 ′ , . . . , x m ′ } S'=\{x'_1,x'_2,...,x'_m\} S′={x1′,x2′,...,xm′},然后使用octree对采样点 S ′ S' S′进行编码,从而能以较低的比特率传输采样点;同时, S ′ S' S′的octree编码被进一步解码回采样点 { x ( 1 ) ′ , x ( 2 ) ′ , . . . , x ( m ) ′ } \{x'_{(1)},x'_{(2)},...,x'_{(m)}\} {x(1)′,x(2)′,...,x(m)′}。
对于每个解码得到的采样点 x ( i ) ′ x'_{(i)} x(i)′,使用KNN可以得到其 K K K个最近邻点 { x i 1 , . . . , x i K } \{x_i^1,...,x_i^K\} {xi1,...,xiK}。最终 S S S的分块由 K K K个近邻点相对于中心采样点的相对位置组成 S ( i ) = { x i 1 − x ( i ) ′ , . . . , x i K − x ( i ) ′ } S_{(i)}=\{x_i^1-x'_{(i)},...,x_i^K-x'_{(i)}\} S(i)={xi1−x(i)′,...,xiK−x(i)′}。
在获得分块后,IPDAE还将每个输入点云的比例归一化。具体来说,每个点云的中心点被移动到 ( 0.5 , 0.5 , 0.5 ) (0.5,0.5,0.5) (0.5,0.5,0.5),然后其坐标被缩放到 [ 0 , 1 ] [0,1] [0,1]。在测试时,解码器的最终输出结果还需要被转换为原始中心点并进行相应的缩放。
此外,为了减少点云密度对基于Pointnet的自编码器的影响。作者对各个分块做以下处理:
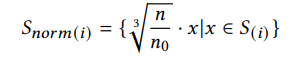
其中 𝑛 𝑛 n 表示输入点云中的点的数量, 𝑛 0 𝑛_0 n0表示参考量常数(实验中设置为1024)。每个重建的分块将被执行相应的逆变换。
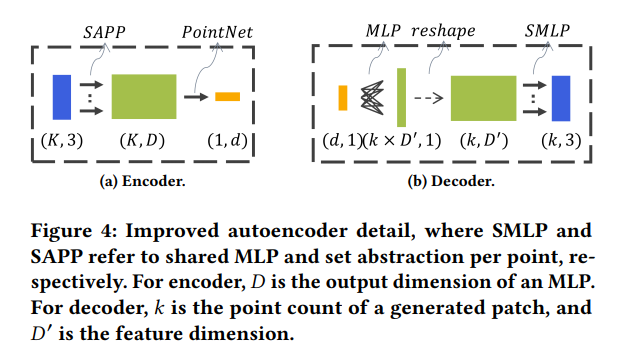
IPDAR的自编码器的结构如图4所示,相比于PDAE采用了更深的解码器以提高解码能力。
每个分块 S ( i ) S_{(i)} S(i)都经过自编码器进行编码。
在解码器一端,首先通过octree解码得到各个采样中心点的位置坐标 S ~ ′ = { x ( 1 ) ′ , x ( 2 ) ′ , … , x ( m ) ′ } \widetilde{S}^{\prime}=\{x_{(1)}^{\prime}, x_{(2)}^{\prime}, \ldots, x_{(m)}^{\prime}\} S ′={x(1)′,x(2)′,…,x(m)′}。对于每个分块,自编码器的重建结果可以表示为: S ~ ( i ) = { ( x i 1 − x ( i ) ′ ) ′ , ( x i 2 − x ( i ) ′ ) ′ , … , ( x i K − x ( i ) ′ ) ′ } \widetilde{S}_{(i)}=\{(x_{i}^{1}-x_{(i)}^{\prime})^{\prime},(x_{i}^{2}-x_{(i)}^{\prime})^{\prime}, \ldots,(x_{i}^{K}-x_{(i)}^{\prime})^{\prime}\} S (i)={(xi1−x(i)′)′,(xi2−x(i)′)′,…,(xiK−x(i)′)′}其中: ( x i K − x ( i ) ′ ) ′ (x_{i}^{K}-x_{(i)}^{\prime})^{\prime} (xiK−x(i)′)′表示重建分块中 K K K个近邻点相对于中心采样点的位置。结合octree解码结果和自解码器的解码结果,我们可以重建第 𝑖 𝑖 i个分块: S ^ ( i ) = { ( x i 1 − x ( i ) ′ ) ′ + x ( i ) ′ , ( x i 2 − x ( i ) ′ ) ′ + x ( i ) ′ , … , ( x i K − x ( i ) ′ ) ′ + x ( i ) ′ } \hat{S}_{(i)}=\{(x_{i}^{1}-x_{(i)}^{\prime})^{\prime}+x_{(i)}^{\prime},(x_{i}^{2}-x_{(i)}^{\prime})^{\prime}+x_{(i)}^{\prime}, \ldots,(x_{i}^{K}-x_{(i)}^{\prime})^{\prime}+x_{(i)}^{\prime}\} S^(i)={(xi1−x(i)′)′+x(i)′,(xi2−x(i)′)′+x(i)′,…,(xiK−x(i)′)′+x(i)′}。合并所有分块即可得到整个重建点云 S ^ \hat{S} S^
PDAE通过逐块( patch-by-patch)的方式训练点云自编码器(由所有点云得到分块组成的训练集,再从中取batch_size个分块进行训练,各个分块不一定属于同一个点云),在测试时使用训练后的自编码器压缩整个点云的所有分块。在IPDAE中,作者集成了压缩和训练过程,以逐点云( point-cloud by point-cloud)的方式训练自编码器,即每次迭代训练都是用一个点云的所有分块:
-
对所有分块使用熵模型,直接估计整个点云的比特率
-
使用整个完整形状的点云的Chamfer距离作为失真度量。Chamfer距离 D c d D_{cd} Dcd定义如下
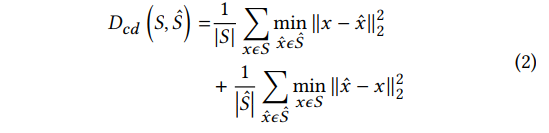
其中 x x x是原始点集 𝑆 𝑆 S中的一个点, 和 x ^ \hat{x} x^表示来自重建点集 S ^ \hat{S} S^的点。 -
使用 L o s s = D c d + λ R Loss = D_{cd}+\lambda R Loss=Dcd+λR对压缩模型进行端到端训练。
熵编码的可学习上下文模型
对每个分块进行编码后,我们可以得到点云的潜在表示 y ∈ R m × d y\in \mathbb{R}^{m\times d} y∈Rm×d,其中 d d d表示各个分块的潜在表示的特征维度。
定义 y ( i ) j y_{(i)j} y(i)j作为第(i)个补丁的第 j j j个元素。给定由正奇数表示的量化级别 L L L ,IPDAE量化每个潜在表示的元素为:
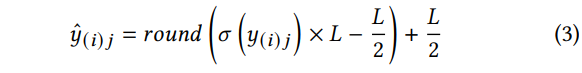
其中 1 ≤ i ≤ m , 1 ≤ j ≤ d 1\le i\le m,1\le j\le d 1≤i≤m,1≤j≤d, σ \sigma σ为sigmoid函数。 y ^ ( i ) j ∈ { 0 , 1 , … , L − 1 } ⊂ Z \hat{y}_{(i) j} \in\{0,1, \ldots, L-1\} \subset Z y^(i)j∈{0,1,…,L−1}⊂Z
训练期间的反向传播的梯度计算为:

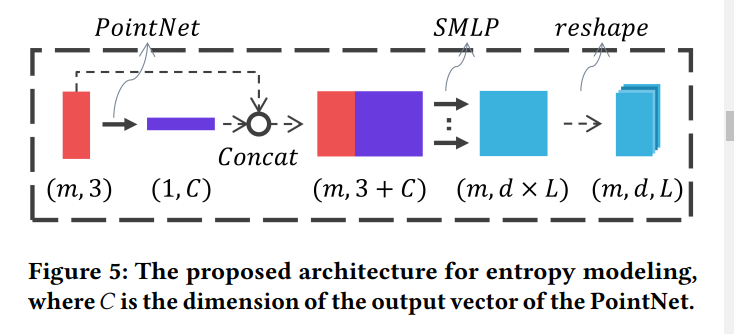
基于采样中心点,使用图5神经网络预测潜在表示每一个元素 y ^ ( i ) j \hat{y}_{(i)j} y^(i)j的概率质量函数 p ( i ) j p_{(i)j} p(i)j。由于 y ^ ( i ) j \hat{y}_{(i)j} y^(i)j由 L L L个可能的量化值,网络的输出维度为: ( m × d × L ) (m\times d\times L) (m×d×L)。对最后一个维度使用softmax,以保证:
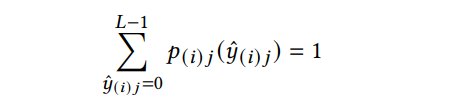
各个元素 y ^ ( i ) j \hat{y}_{(i)j} y^(i)j的分布为:
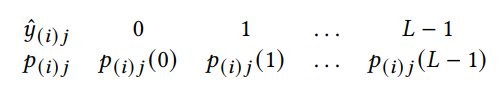
分块潜在表示的比特率估计表达式如下:
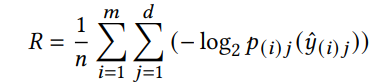
其中 p ( i ) j ( y ^ ( i ) j ) p_{(i)j}(\hat{y}_{(i)j}) p(i)j(y^(i)j)为量化元素 y ^ ( i ) j \hat{y}_{(i)j} y^(i)j实际值的概率。在测试阶段,使用预测的概率质量函数 p ( i ) j p_{(i)j} p(i)j进行算术编码和解码。
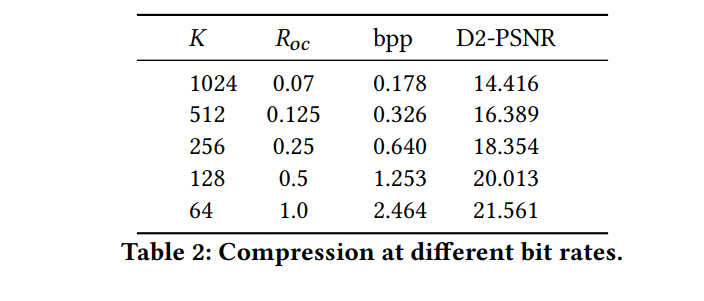
作者通过改变每个分块的分辨率( K K K) 和octree编码比特流的比特率( R o c R_{oc} Roc)来实现不同比特率的压缩
对抗学习
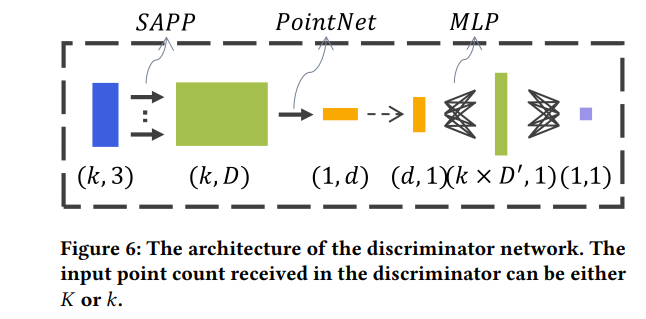
以上面预训练的自编码器作为生成器,以图6的网络作为判别器,使用WGAN进一步训练自编码器,判别器损失:
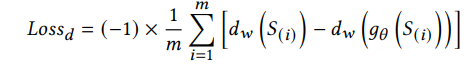
生成器损失:
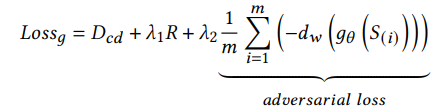
均匀性度量
这篇文章还提出了一个均匀性度量,它计算每个点到其点云的距离的方差。计算公式如下:
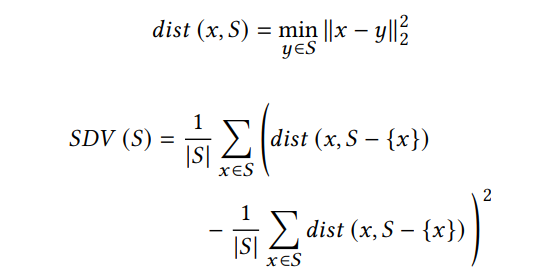
其中dist为点 x x x到点集的距离,表示该点与其最近相邻点之间的距离。自距离方差(SDV)表示基于点对点距离的距离方差(越小越均匀)。最后,均匀性系数被定义为重建点云的均匀性与源点云的均匀性与之比:
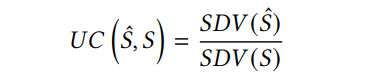
以比率表示的度量更直观:UC为0表示重建点云的近似绝对均匀性,UC为1表示与原始点云相似的均匀性,而UC大于1表示比原始点云更不均匀性。UC值越低,点集分布越均匀。
实验结果
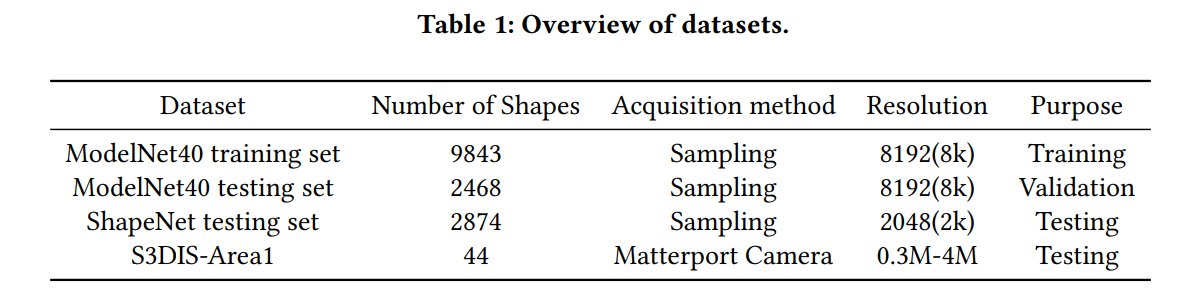
Visualization of Training Process

Compression performance comparison

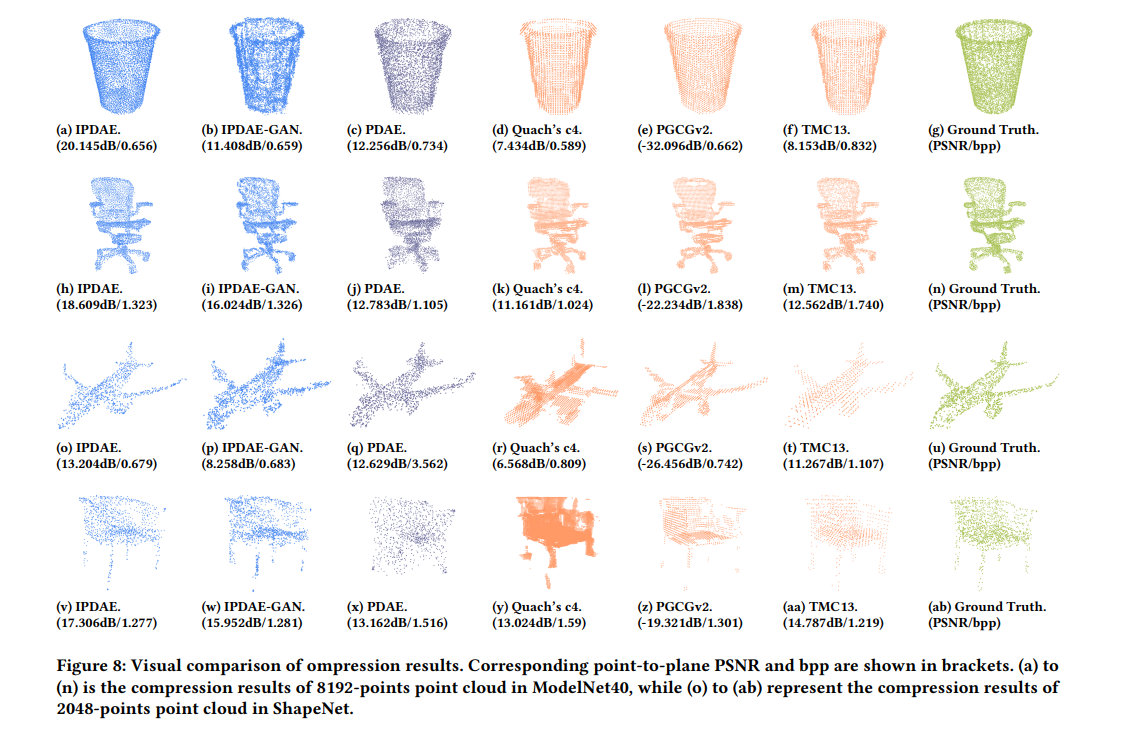

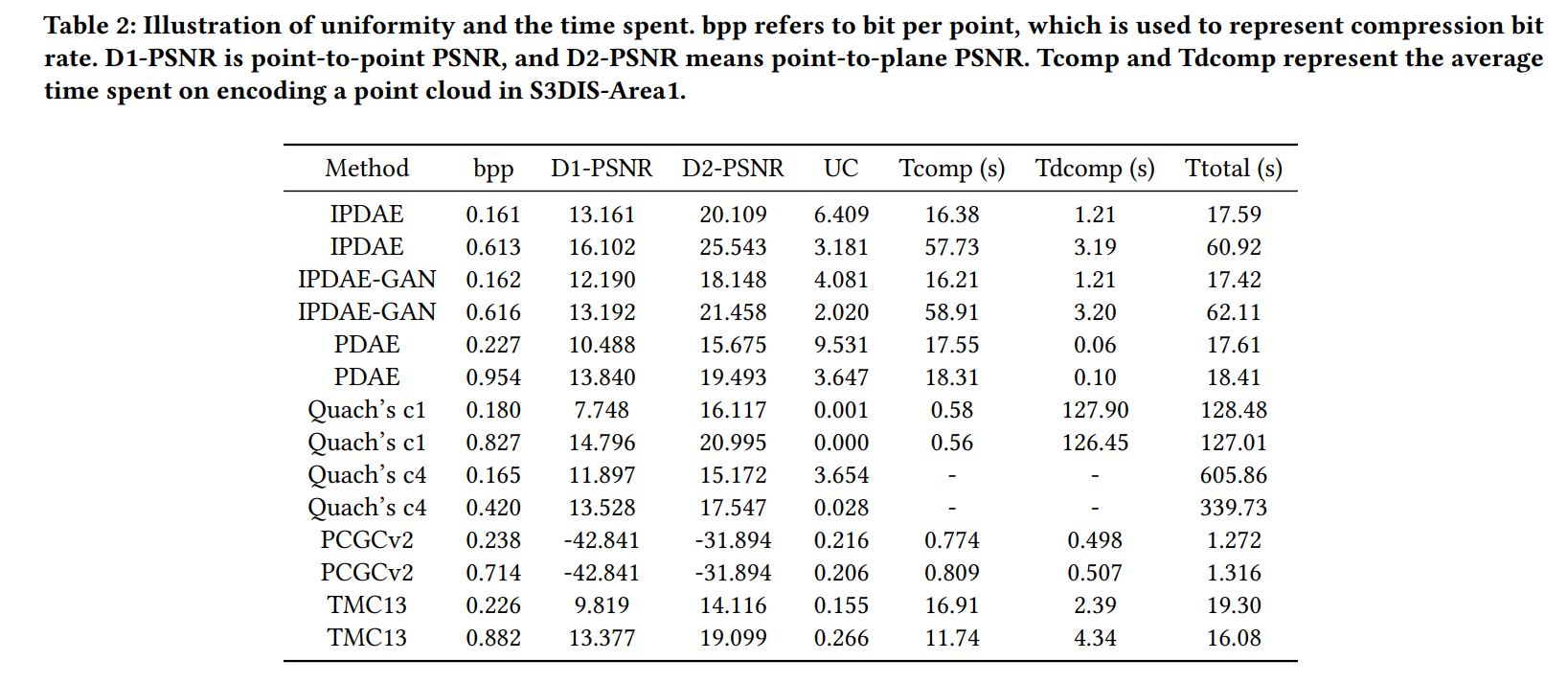
Additional Comparison with PCGCv2

Ablation Study
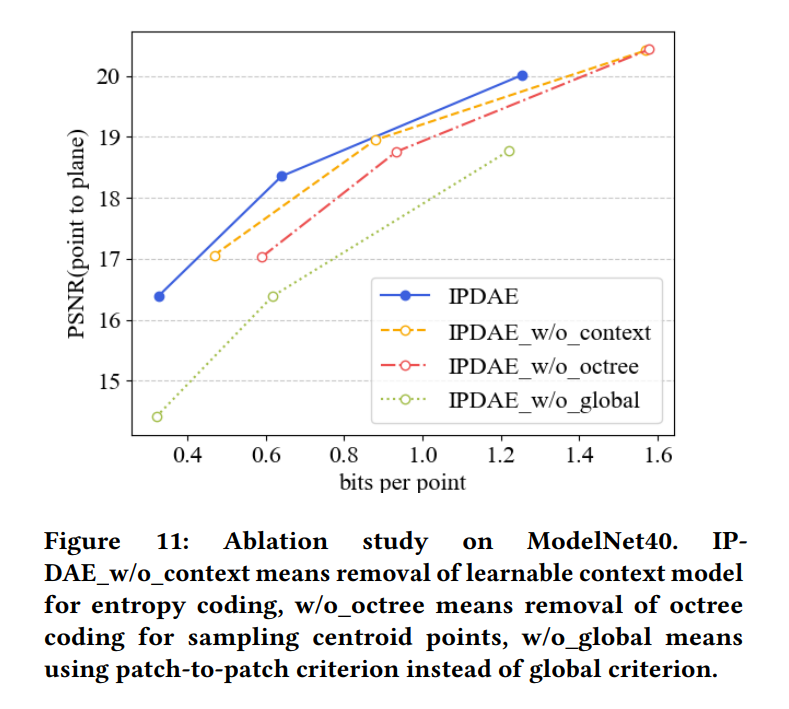
这篇关于IPDAE: Improved Patch-Based Deep Autoencoder for Lossy Point Cloud Geometry Compression的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









