2021_ICCV_Gradient Distribution Alignment Certificates Better Adversarial Domain Adaptation

Abstract

处理无监督领域适应任务中领域迁移的最新启发式方法是使用对抗学习减少数据分布差异。最近的研究通过将分类器的输出集成到分布散度度量中，改进了传统的具有判别信息的对抗域适应方法。然而，他们仍然遭受着对抗学习的均衡问题，即使判别器完全混淆，也无法保证两个分布之间有足够的相似性。为了克服这个问题，我们提出了一种新的特征梯度分布对齐方法( FGDA ) ( 1 )。我们从理论和实证两方面论证了我们方法的合理性。特别地，我们表明通过约束两个域的特征梯度具有相似的分布，可以减少分布差异。同时，我们的方法在理论上保证了可以获得比传统对抗域自适应方法更紧的目标样本误差上界。通过将所提出的方法与现有的对抗域适应模型集成，我们在两个真实的基准数据集上实现了最先进的性能。

1. Introduction

深度神经网络( Deep Neural Networks，DNNs )在图像分类[ 12、16]、目标检测[ 11、26]和语义分割[ 21、24]等各种应用中取得了令人印象深刻的性能。然而，由于数据分布偏移问题表现在许多不同的方面，如样本选择偏差[ 5 ]、类分布偏移[ 19 ]、协变量偏移[ 29 ]等，DNNs可能无法很好地对新数据进行泛化。无监督领域适应( UDA )旨在通过访问有标签的源数据和无标签的目标数据来解决领域迁移问题[ 8 ]。基本目标是推断领域不变的表示[ 32 ]。
在当前的深度架构中，对抗域自适应( ADA )方法[ 25、22、30、15]被广泛研究，并取得了最先进的性能。领域对抗神经网络( Domain-Adversarial Neural Networks，DANN )作为一项开创性的工作，将对抗学习和领域适应集成到一个极大极小不等式游戏中[ 8 ]。学习一个域判别器来区分源分布和目标分布，而深度分类模型学习对域判别器不可区分的可迁移表示。最近的成功方法表明，区分性分布对齐可以实现更好的域适应[ 25、22、30、15、27、38]。这些研究的核心思想是利用分类器输出或预测提供的判别信息进行目标判别表示学习。
尽管判别信息有助于提升域适应的性能，但我们认为域转换仍然是一个主要的挑战，限制了性能的进一步提升。这样的缺点来自于对抗学习的平衡挑战[ 2 ]，即使判别器完全混淆，也不能保证两个分布充分相似，如图1 ( a )和( b )所示。
为了解决这个问题，我们提出了一种称为特征梯度分布对齐( FGDA )的新方法，以进一步减少域偏移。具体来说，FGDA通过特征提取器和判别器之间的对抗学习，学习减少特征梯度在两个域之间的分布差异。当达到均衡时，特征分布差异的值可以最小。
我们借用[ 10、1、37]对对抗扰动的洞察来简单描述所提出方法的原理。样本的输入梯度可以认为是对输入扰动最小的敏感方向，从而最大程度地改变模型的输出[ 1 ]。直觉上，一个样本的特征梯度方向可能倾向于指向其最近决策边界的区域。此外，由于特征梯度指向高度复杂的决策边界(在DNNs中通常可以看到)的不同部分，因此它们之间可能存在显著差异；距离较近的特征梯度可能具有相似的方向。因此，对齐特征梯度鼓励学习执行两个域分布的潜在表示来保持距离。因此，可以减少特征分布差异。由于我们方法的优点，与传统的域适应方法相比，即使两个域的平均特征接近，我们的方法也能进一步减少域偏移，如图1所示，这也在后面的3.7节中进行了理论分析。重要的是，我们进一步证明了对齐特征梯度比传统的对抗域适应方法在目标样本上的期望误差上界更紧。
总之，我们的主要贡献如下：

• 我们提出了一种新的方法FGDA，使用对抗学习来对齐特征梯度，以减少分布差异。与传统方法相比，即使源和目标分布的均值接近，我们的模型也能进一步减小域偏移。
• 我们从理论和实证两个方面证明了我们方法的有效性。特别地，我们证明了我们的方法可以获得比传统的域适应方法更紧的上界。
• 我们进行了大量的实验，以表明所提出的方法不仅能够减少域差异，而且与当前基于特征的对抗域适应方法相比，具有一致的改进。特别地，我们的方法在UDA任务上取得了最先进的性能。

2.Related Work

对抗域自适应( ADA )方法[ 7、34、35]不仅提供了理论保证，而且取得了最先进的性能，最近被广泛研究。受生成式对抗网络( Generative Adversarial Networks，GANs ) [ 9 ]的启发，这些方法在极大极小不等式游戏中学习一个域不变的特征，其中一个特征提取器学习欺骗一个域判别器，而判别器则努力不被欺骗[ 8 ]。与这些特征级方法相比，生成式像素级自适应模型在原始像素空间中执行分布对齐，通过使用图像到图像的转换技术[ 40、20、14、28]将源数据转换到目标域。
尽管它们对从分类[ 7、35、20]到分割[ 28、33、14]的各种任务具有普遍的有效性，但它们不得不面对对抗学习的平衡问题[ 2 ]。因此，当数据分布中存在复杂的多模态结构时，香草ADA方法可能无法捕获这些多模态结构，从而实现无模式失配的分布判别比对[ 22 ]。
为了进一步减少域偏移，最近成功的ADA方法致力于实现区分性分布对齐。其中一种被广泛研究的方法被命名为类条件ADA，它将领域分类器对特征和相应的预测同时进行[ 25、22、30、15]。这些方法旨在近似两个域之间的联合分布对齐，以实现具有判别性的目标特征。另一类ADA研究依靠两个分类器来衡量两个领域的分布差异。利用两个分类器预测的不一致来检测不明确属于某个类别的非鉴别特征。通过与特征提取器进行极大极小不等式博弈，两个分类器优化决策边界以缓解类内领域差异[ 27、38]。
尽管上述努力促进了更好的分布对齐，但对抗训练不可避免的平衡挑战仍然限制了当前ADA方法的性能。为了缓解这一问题，我们在这一研究方向上更进一步，提出了一种特征梯度分布对齐方法，该方法可以在理论上更严格的误差上界下进一步减少分布差异。注意到一个并行工作[ 6 ]与我们的想法不谋而合，并研究了类似的方法。我们独立地利用梯度对齐，但从不同的角度和不同的理论分析。

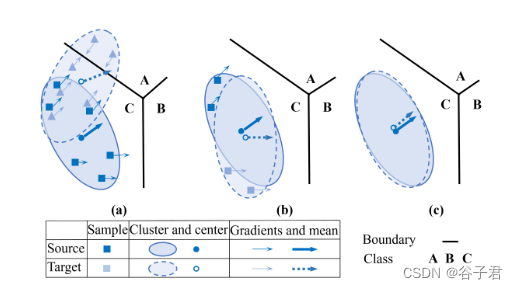
见图1。特征梯度分布对齐( Fgda )示意图。( a ) - ( c )：当两个域的特征因域偏移较大而分布差异较大时，它们在非重叠区域的梯度可能分散在高度复杂的决策边界的不同部分，从而导致较大的梯度分布差异。通过梯度对齐，扩大重叠区域以减少域偏移。( a ) ~ ( b )：当两个均值特征足够接近时，传统对抗域适应方法测量的域偏移趋于零。在这种情况下，常规方法无法进一步减小域偏移。( b ) - ( c )：即使两个均值特征之间的距离较小，由于非重叠区域的梯度明显不同，我们的方法(在特征梯度差异方面)度量的域偏移仍然可以被观察到。FGDA可以证明进一步的域移减少。

3. Methodology

3.1. Preliminaries

对于香草无监督域适应( UDA )任务，给定源域${\mathcal{D}}_s$中 $n_s$ 个标记样本 { ( x i s , y i s ) } i = 1 n s \left\{\left(x_i^s, y_i^s\right)\right\}_{i=1}^{n_s} {(xis​,yis​)}i=1ns​​ ，其中$x_i^s\in {\mathcal{X}}_s,y_i^s\in {\mathcal{Y}}_s$和目标域${\mathcal{D}}_t$中$n_t$ 个未标记样本${\left\{x_j^t\right\}}_{j=1}^{n_t}$ ，其中$x_j^t\in {\mathcal{X}}_t$。UDA的目标是学习一个分类模型来预测目标域标签${\left\{y_j^t\right\}}_{j=1}^{n_t}$ ，其中 $y_j^t\in {\mathcal{Y}}_t$。整个分类模型由特征提取器$G(\cdot )$和任务分类器$C(\cdot )$组成，期望能够保证分类准则$\mathcal{L}(\cdot ,\cdot )$具有较低的目标风险${\mathbb{E}}_{\left({\mathbf{x}}^t,y^t\right)\sim {\mathcal{D}}_t}\left[\mathcal{L}\left(C\left(G\left({\mathbf{x}}^t\right)\right),y^t\right)\right]$。
特征提取器$G(\cdot )$通过${\mathbf{x}}^s$ and ${\mathbf{x}}^t$ 将${\mathbf{x}}^s$ and ${\mathbf{x}}^t$编码到一个公共特征空间，其中$G(\cdot )$可以是任意类型的神经网络，$f^s,f^t\in {\mathbb{R}}^D$表示源域和目标域的D维特征向量。对于$K$-way分类任务，将$f^s$ and $f^t$ 送入任务分类器进行预测${\mathbf{z}}^s=C\left(f^s\right),{\mathbf{z}}^t=C\left(f^t\right)$，其中${\mathbf{z}}^s,{\mathbf{z}}^t\in {\mathbb{R}}^k$ 为得分向量。利用源域的真实标注数据，通过最小化标准交叉熵损失来训练分类模型：
$${\mathcal{L}}_{\mathrm{src}}=-{\mathbb{E}}_{{\mathbf{x}}^s\in {\mathcal{X}}_s,y^s\in {\mathcal{Y}}_s}\sum _{k=1}^K{q}_k\log {\delta }_k\left(z^s\right)$$
其中${\delta }_k\left(z^s\right)=\frac{\exp \left(z_k^s\right)}{{\sum }_l\exp \left(z_l^s\right)}$ 表示向量$z^s$的softmax输出中的第k个元素，$q$是 $y^s$ 的one-of$K$编码，其中$q_k$对正确类是’ 1 ‘，其余类是’ 0 '。目标是预测目标样本的标签，记为${\hat{y}}^t={\mathrm{argmax}}_k\left(\delta \left(z_k^t\right)\right)$.

3.2. Framework Overview

我们提出了一个称为特征梯度分布对齐( FGDA )的框架来减少域偏移，如图2所示。我们的核心部分是对抗学习的一部分，用于对齐特征提取器和梯度判别器相互竞争的两个域的特征梯度分布。为了进一步推广我们提出的方法，我们提出了Jacobian正则化项${\Vert J\left(f^s\right)\Vert }_F^2$和自监督伪标记机制，分别用于提高模型泛化性和伪标记质量。此外，我们将说明如何将我们的方法部署在传统的ADA方法上，例如。DANN [ 8 ]、CDAN [ 22 ]和MDD [ 38 ]，进一步缩小分布差异。

3.3. Feature Gradient Distribution Alignment

为了获得两个域的特征梯度，我们需要计算目标样本的损失。在训练阶段，利用分类模型的预测结果${\hat{y}}^t$作为在线伪标注计算目标样本的损失${\mathcal{L}}_{\text{tgt }}\left(C\left(G\left({\mathrm{x}}^t\right)\right),{\hat{y}}^t\right)$。
注意到目标域中的损失只用于梯度计算而不是训练整个分类模型。通过反向传播机制，源域和目标域的特征梯度向量可以计算为：
$$\mathbf{g}\left(x^s,G\right):=\left[\frac{\partial {\mathcal{L}}_{\mathrm{src}}}{\partial G{\left(x^s\right)}_1}\cdots \frac{\partial {\mathcal{L}}_{\mathrm{src}}}{\partial G{\left(x^s\right)}_d}\cdots \frac{\partial {\mathcal{L}}_{\mathrm{src}}}{\partial G{\left(x^s\right)}_D}\right]$$
$$g\left(x^t,G\right):=\left[\frac{\partial {\mathcal{L}}_{\mathrm{tgt}}}{\partial G{\left(x^t\right)}_1}\cdots \frac{\partial {\mathcal{L}}_{\mathrm{tgt}}}{\partial G{\left(x^t\right)}_d}\cdots \frac{\partial {\mathcal{L}}_{\mathrm{tgt}}}{\partial G{\left(x^t\right)}_D}\right]$$
其中 $G{\left(x^s\right)}_d$ 和 $G{\left(x^t\right)}_d$ 表示特征向量(为方便起见,使用 $f_d^s$ and $f_d^t$ 的第d个元素，$\mathbf{g}\left(x^s,G\right)$ and $\mathbf{g}\left(x^t,G\right)$ 表示对应的梯度向量(为了方便使用$g^s$ and $g^t$ )。
为了实现梯度分布对齐的目标，采用了特征提取器和判别器(作为散度估计量)相互竞争的对抗学习。具体来说，判别器是预测源域和目标域特征梯度的域标签，而特征提取器则学习混淆判别器。当达到均衡时，特征分布差异达到最小值。
我们提出的方法中特征梯度对齐的主要目标可以表述为：
$$\begin{array}{rl}\underset{G}{\min }\underset{D_g}{\max }{\mathcal{L}}_{adv}& ={\mathbb{E}}_{{\mathbf{x}}^t\in X^t}\left[\log D_g\left(g\left({\mathbf{x}}^t,G\right)\right)\right]\\ & +{\mathbb{E}}_{{\mathbf{x}}^s\in X^s}\left[\log \left(1-D_g\left(g\left({\mathbf{x}}^s,G\right)\right)\right)\right]\end{array}$$
其中 $D_g(\cdot )$ 是判别器，它输出梯度向量来自目标域的概率。
所提方法的原理如图3所示。最初，由于较大的域偏移，来自不同域的两组点分布差异很大，特征梯度指向高维空间中高度复杂的决策边界的不同部分。因此，两个域的大部分特征梯度明显不同，导致特征梯度分布差异较大。通常情况下，距离较近或较小区域内的特征具有相似的梯度。因此，梯度对齐可以迫使这两组点相互移动并停留在梯度相近的小区域，如图3中的红色虚线圆。换句话说，可以减少域偏移。为了进一步说明域偏移会导致较大的特征梯度差异，我们在图3中进行了分析，其中绘制了每个类在两个域之间的平均梯度距离(注意正常化)
相比之下，对于传统的基于特征的ADA方法，如图1所示，域偏移由判别器$D_g:$衡量：$=\mid E_{\mathbf{f}\sim \widetilde{D_{\mathcal{S}}}}{D}_g(f)-$ $E_{\mathbf{f}\sim {\mathcal{D}}_{\mathcal{T}}}{D}_g(\mathbf{f})\mid$，其中’ ${\tilde{\mathcal{D}}}_{\mathcal{S}}$和${\tilde{\mathcal{D}}}_{\mathcal{T}}$ 为${\mathcal{D}}_s$ 和${\mathcal{D}}_t$在特征空间的诱导分布。存在常数$\alpha$使得 $dis=\alpha \left|D_g\left(E_{\mathbf{f}\sim \overline{{\mathcal{D}}_{\mathcal{S}}}}f\right)-D_g\left(E_{\mathbf{f}\sim {\mathcal{D}}_{\mathcal{T}}}f\right)\right|$。当平均特征$E_{f\sim \overline{{\mathcal{D}}_{\mathcal{S}}}}f$ 和$E_{f\sim \overline{D_{\mathcal{T}}}}f$ 接近时，传统方法测量的域偏移dis趋于零，从而反向传播到特征提取器的相应梯度趋于零。因此，不能进一步减小畴移。与之不同的是，我们的方法中，区域位移由dis$=\left|E_{\mathbf{f}\in \widetilde{{\mathcal{D}}_{\mathcal{S}}}}{D}_g\left({\nabla }_{\mathbf{f}}\mathcal{L}\right)-E_{\mathbf{f}\in \widetilde{{\mathcal{D}}_{\mathcal{T}}}}{D}_g\left({\nabla }_f\mathcal{L}\right)\right|$来度量。类似地，存在常数$\beta$使得dis our $=$ $\beta \left|D_g\left(E_{\mathbf{f}\sim \widetilde{{\mathcal{D}}_{\mathcal{S}}}}{\nabla }_{\mathbf{f}}\mathcal{L}\right)-D_g\left(E_{\mathbf{f}\sim \widetilde{{\mathcal{D}}_{\mathcal{T}}}}{\nabla }_{\mathbf{f}}\mathcal{L}\right)\right|$.根据图1，即使两个均值特征之间的距离很小，由于非重叠区域存在明显的不同梯度，我们的方法$di{s}_{\text{our }}$ 测量的域偏移仍然可以很大。因此，域偏移可以进一步减小。
定义投入产出雅克比矩阵为：
$$J_{k;d}\left(f^s\right)\equiv \frac{\partial z_k}{\partial f_d^s}\left(f^s\right)$$
其中$z_k^s$和$f_d^s$ 分别表示特征$f^s$在源域的第k个评分值$z^s$和d个元素。则雅克比正则化定义为：

$$\underset{G,C}{\min }{L}_{jr}={\Vert J\left(f^s\right)\Vert }_{\mathrm{F}}^2\equiv \left\{\sum _{d,k}{\left[J_{k;d}\left(f^s\right)\right]}^2\right\}$$

3.4. Feature-level Jacobian Regularization

多项工作表明，判别性特征有助于提高分布对齐[ 30、27、35]的性能。为了学习更具判别性的特征，本文采用梯度正则化方法最大化分类间隔[ 23、13]。为此，Hoffman等人提出了最小化输入输出梯度矩阵的范数，称为Jacobian矩阵[ 13 ]。类似地，我们在特征层面采用Jacobian正则化，使得特征提取器能够学习到更多远离决策边界的判别性特征，同时分类器能够扩大分类边界。

3.5. Self-supervised Pseudo-labeling

尽管使用模型预测的在线伪标注进行梯度对齐是可行的，但是错误的预测会产生次优的梯度分布，从而阻碍梯度对齐达到最优的性能。
为了在目标域中获得高质量的伪标注，我们将一种无监督的方法集成到我们的框架中，捕获不同类的目标分布，称为自监督伪标记[ 18 ]。在初始训练阶段结束后，对每一个固定的迭代次数执行该策略，生成离线伪标签集合${\tilde{\mathcal{Y}}}_t$ (利用特征质心预测当前样本的离线伪标注)。一旦得到离线的伪标注，则${\tilde{y}}_t\in {\tilde{\mathcal{Y}}}_t$将代替在线的伪标签(在线伪标注是用分类器对当前样本进行预测) (${\hat{y}}_t$ )对每个目标样本进行特征梯度计算。
每个类的特征分布的质心也被认为是一个原型表示，其分布应该出现在分类器自信地预测大量样本的区域。质心的更新类似于k - means聚类，通过分类器的置信度对每个目标特征进行加权：
$${\mathbf{c}}_k^{(0)}=\frac{{\sum }_{{\mathbf{x}}^t\in {\mathcal{X}}_t}{\delta }_k\left(\tilde{C}\left(\tilde{G}\left({\mathbf{x}}^t\right)\right)\right)\tilde{G}\left({\mathbf{x}}^t\right)}{{\sum }_{{\mathbf{x}}^t\in {\mathcal{X}}_t}{\delta }_k\left(\tilde{C}\left(\tilde{G}\left({\mathbf{x}}^t\right)\right)\right)}$$
其中， $\tilde{G}(\cdot )$ 和 $\tilde{C}(\cdot )$ 在上一次迭代中已经过训练，用于在线预测伪标注。每个目标样本的离线伪标签被赋予最近质心的标签：

$${\tilde{y}}^t=\arg \underset{k}{\min }{M}_f\left(\tilde{G}\left(x_t\right),c_k^{(0)}\right)$$
式中： $M_f(a,b)$ 为$a$ 和$b$之间的余弦距离度量。最后，根据新的伪标签确定类别质心：
$$\begin{array}{rl}{c}_k^{(1)}& =\frac{{\sum }_{{\mathbf{x}}^t\in {\mathcal{X}}_t}\mathbb{I}\left({\tilde{y}}^t=k\right)\tilde{G}\left({\mathbf{x}}_t\right)}{{\sum }_{{\mathbf{x}}^t\in {\mathcal{X}}_t}\mathbb{I}\left({\tilde{y}}^t=k\right)},\\ {\tilde{y}}^t& =\arg \underset{k}{\min }{M}_f\left(\tilde{G}\left({\mathbf{x}}^t\right),{\mathbf{c}}_k^{(1)}\right),\end{array}$$
式中： $\mathbb{I}$ 为二元指示函数。当${\tilde{y}}^l=k$时，函数输出1。式中：9时，类质心和伪标注交替更新多轮。实际观测到，即使这些参数更新一次，仍然可以提高伪标注的质量。

3.6. Overall Learning Objective

为了总结前面的成分，我们在下面给出了总的训练损失。在初始训练阶段，采用特征梯度分布对齐和特征级Jacobian正则化对模型进行训练。相应的目标可以表述为：
$$\underset{G,C}{\min }\underset{D_g}{\max }\left({\mathcal{L}}_{\text{src }}+{\lambda }_1{\mathcal{L}}_{adv}+{\lambda }_2{\mathcal{L}}_{jr}\right),$$
其中 ${\lambda }_1,{\lambda }_2\ge 0$是两个平衡参数.首先利用在线伪标注( ${\hat{y}}^t$ 计算目标样本的特征梯度${\mathbf{g}}^t$，得到式( 1 )的${\mathcal{L}}_{adv}$。4 .经过固定次数的迭代后，自监督伪标记参与训练。然后将${\mathcal{L}}_{adv}$改为${\tilde{\mathcal{L}}}_{adv}$，其中 ${\mathbf{g}}^t$ 由离线伪标注${\tilde{y}}^t$ 和 ${\mathcal{L}}_{\text{tgt }}\left(\cdot ,{\tilde{y}}^t\right)$给出。综上，完全损失为：

$$\underset{G,C}{\min }\underset{D_g}{\max }{\mathcal{L}}_{FGD\Lambda }={\mathcal{L}}_{\mathrm{src}}+{\lambda }_1{\tilde{\mathcal{L}}}_{adv}+{\lambda }_2{\mathcal{L}}_{jr}.$$
为了展示我们方法的优势，我们将FGDA与一些传统的基于特征的ADA方法，如DANN [ 8 ]，CDAN [ 22 ]和MDD [ 38 ] )相结合。组合的简单方法是直接添加一个梯度判别器并重用它们的结构。综合训练损失为：
$${\mathcal{L}}_{FGDA+\text{ fada }}={\mathcal{L}}_{\mathrm{src}}+{\lambda }_1{\tilde{\mathcal{L}}}_{adv}+{\lambda }_2{\mathcal{L}}_{jr}+{\lambda }_3{\mathcal{L}}_{\text{fada }}$$
其中${\mathcal{L}}_{\text{fada }}$是基于特征的ADA模型的对抗损失，${\lambda }_3$是其平衡参数。

3.7. Model Analysis

在这一部分，我们对提出的FGDA方法进行了理论和实证分析。首先考虑特征 $f=G(x)$ 和一族源分类器$C$分别在固定的表示空间$\mathcal{F}$和假设空间$\mathcal{H}$上。假设C∈H在源域上的误差为${ϵ}_S(C)={\mathrm{E}}_{\mathbf{f}\sim \widetilde{{\mathcal{D}}_S}}[C(\mathbf{f})\ne y]$，其中${\tilde{\mathcal{D}}}_S$ 表示源数据分布 ${\mathcal{D}}_S$的诱导特征分布，$y$是特征f的标签。假设$C_1,C_2\in \mathcal{H}$ 之间的分歧由${ϵ}_S\left(C_1,C_2\right)={\mathrm{E}}_{\mathbf{f}\sim {\overline{\mathcal{D}}}_S}\left[C_1(\mathbf{f})\ne C_2(\mathbf{f})\right]$给出。为了从未标记数据中估计分布散度，引入了一个理想的联合假设$C^{\ast }={\mathrm{argmin}}_C{ϵ}_S(C)+{ϵ}_T(C)$来最小化两个域上的联合误差。然后，给出了目标误差的概率界
$${ϵ}_T(C)\le {ϵ}_S+\lambda +\left|{ϵ}_T\left(C,C^{\ast }\right)-{ϵ}_S\left(C,C^{\ast }\right)\right|,$$
其中$\lambda ={ϵ}_S\left(C^{\ast }\right)+{ϵ}_T\left(C^{\ast }\right)$是理想联合假设的误差.
为了证明我们提出的方法FGDA的有效性，我们表明我们的方法可以获得比传统的域适应方法更紧的目标域误差上界。主要理论见定理1和定理2。
定理1设$G$是从$\mathcal{X}$到$\mathcal{F}$的固定表示函数，$\mathcal{H}$是VC维$d$的假设空间.如果将$G$应用于一个${\mathcal{D}}_s$生成一个大小为$m$的随机标记样本.特征f取自" ${\tilde{\mathcal{D}}}_S$ or ${\tilde{\mathcal{D}}}_T$，对应的标签为$y$。令 ${\tilde{\mathcal{U}}}_S,{\tilde{\mathcal{U}}}_T$分别表示从 ${\tilde{\mathcal{D}}}_S$ and ${\tilde{\mathcal{D}}}_T$中抽取的大小为$m^{\prime }$的未标记样本集合。则对每个$C\in \mathcal{H}$，至少有$1-\delta$ (在样本的选择上)的概率：
$$\begin{array}{rl}{ϵ}_T(C)\le & {\widehat{ϵ}}_S(C)+\lambda +d_{\nabla }\left({\tilde{\mathcal{U}}}_S,{\tilde{\mathcal{U}}}_T\right)\\ & +\frac{4}{m}\sqrt{\left(d\log \frac{2em}{d}+\log \frac{4}{\delta }\right)}\\ & +4\sqrt{\frac{d\log \left(2m^{\prime }\right)+\log \left(\frac{4}{\delta }\right)}{m^{\prime }}}\\ & =\text{ const }+d_{\nabla }\left({\tilde{\mathcal{U}}}_S,{\tilde{\mathcal{U}}}_T\right)\end{array}$$
其中${\widehat{ϵ}}_S(C)$是源样本的经验误差，$\lambda$是一个很小的常数，$e$是自然对数的底，$d_{\nabla }\left({\tilde{\mathcal{U}}}_S,{\tilde{\mathcal{U}}}_T\right)=$ $a{\sup }_{D_g{\mathcal{H}}_D}\left|E_{\mathbf{f}\in {\tilde{\mathcal{U}}}_{\mathcal{S}}}{D}_g\left({\nabla }_{\mathbf{f}}\mathcal{L}\right)-E_{\mathbf{f}\in {\tilde{\mathcal{U}}}_{\mathcal{T}}}{D}_g\left({\nabla }_{\mathbf{f}}\mathcal{L}\right)\right|$是引入的$\nabla$-distance，$D_g$ 是判别因子，$a=\frac{1}{{\min }_{C(f)\in [0,1]}{\nabla }_C\mathcal{L}(C(f),y)}$ .式中$\mathcal{L}(\cdot )$ 为损失函数。
定理2当$a\le 1$时，我们的方法可以获得比传统的域适应方法更紧的上界：
const $+d_{\nabla }\left({\tilde{\mathcal{U}}}_S,{\tilde{\mathcal{U}}}_T\right)\le$ const $+d_{\mathcal{H}}\left({\tilde{\mathcal{U}}}_S,{\tilde{\mathcal{U}}}_T\right)$, where $d_{\mathcal{H}}\left({\tilde{\mathcal{U}}}_S,{\tilde{\mathcal{U}}}_T\right)={\sup }_{D_g\in {\mathcal{H}}_D}\left|E_{\mathbf{f}\in {\tilde{\mathcal{U}}}_S}{D}_g(\mathbf{f})-E_{\mathbf{f}\in {\tilde{\mathcal{U}}}_{\mathcal{T}}}{D}_g(\mathbf{f})\right|$. 定理1 - 2的证明可参见补充文献.
、定理1 - 2表明，特征梯度分布差异有助于约束测试误差。换句话说，特征梯度对齐可以减少测试误差。更重要的是，更紧的边界保证了我们提出的方法优于传统的域适应方法。
然而，从经验的角度看，直接计算$\nabla$-distance 可能是困难的。在这项工作中，我们借助域判别器$D_g$ 来近似它。具体来说，$D_g$ 试图区分哪些域特征梯度∇f L来自哪个域。${\mathcal{H}}_g$是特征梯度${\nabla }_f\mathcal{L}$上的$\nabla$假设空间.因此，区域偏差$\left|{ϵ}_T\left(C,C^{\ast }\right)-{ϵ}_S\left(C,C^{\ast }\right)\right|$可以上确界于$\nabla$-distance.详细证明可在补充材料中找到。
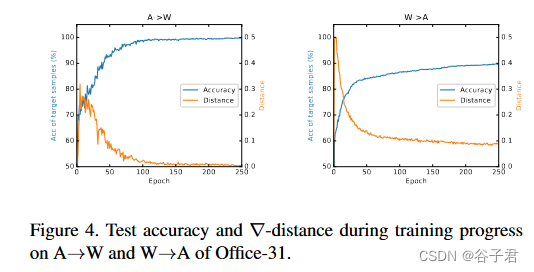
我们在图4中进一步给出了$\nabla$-distance与试验误差的关系。我们考虑一个理想的情况，即目标样本的所有特征梯度都是根据其真实的目标标签计算的。正如观察到的那样，它们之间存在明确的负相关关系。$\nabla$-distance的减小直接导致不同训练历元的测试精度一致提高。直到$\nabla$-distance收敛，A→W和W→A的正确率分别为100 %和90 %。这表明$\nabla$-distance与测试误差高度相关，在两个域之间对齐特征梯度分布类似于用目标伪标注来训练模型。

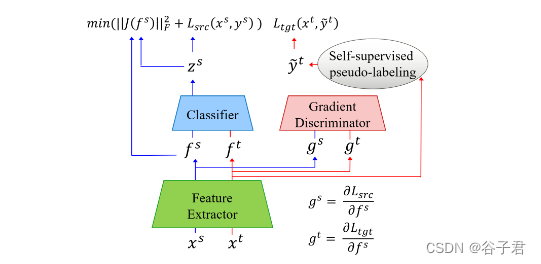
见图2。特征梯度分布对齐的结构。整个结构由多个机制组成：对抗学习(分类器、梯度判别器和特征提取器)、自监督伪标记和Jacobian正则化${\Vert J\left(f^s\right)\Vert }_F^2$，其中后两个机制用于促进对抗学习。

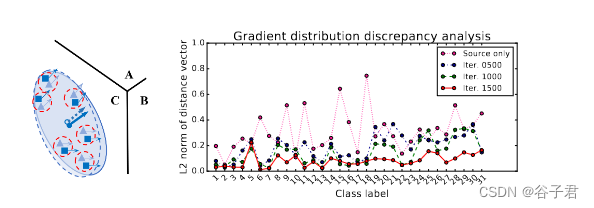
见图3。几何解释：梯度对齐强制两个域的特征停留在梯度相似的小区域(红色虚线圆圈)。数值分析：Office - 31的D→A任务梯度差异分析。

4. Experiments

4.1. Datasets

办公室- 31。Office - 31是一个广泛使用的评价视觉域适应算法的数据集。它包括4 652幅图像和31个类别，分别来自三个不同的领域：Amazon ( A )、Webcam ( W )和DSLR ( D )。我们在六种迁移任务A→W，D→W，W→D，A→D，D→A和W→A上评估了所有方法。
Office - Home是一个更具挑战性的数据集。在办公室和家庭环境中，它由65类15500张图像组成。在四个截然不同的领域：艺术图像( A )、剪贴画( C )、产品图像( P )和真实世界图像( R )上，我们评估了所有的迁移任务。
实施细则。遵循UDA的标准评估协议[ 3 ]，将所有有标签的源和无标签的目标实例作为训练数据。为了公平比较，我们使用与被比较方法相同的网络结构。具体地，所有实验均采用ResNet - 50 [ 12 ]作为主干网络，并采用线性层后跟softmax函数作为类别分类器。对于我们的梯度判别器，它由两个隐藏层组成，分别是一个全连接层，然后是ReLu激活函数和Batch Norm层，以及一个对隐藏特征进行线性变换，然后用sigmoid函数激活的域分类器。对抗学习算法的实现类似于原始的DANN [ 8 ]，在特征梯度上施加反向梯度层。式中：，单独考察FGDA时，${\lambda }_1$取1。FGDA与MDD结合时[ 38 ]，如公式所示。${\lambda }_3$固定为0 . 5，Office - 31和Office - Home分别取 ${\lambda }_1=1$ 和${\lambda }_1=0.5$ 。对于 ${\lambda }_2$，从[ 0.05、0.10、0.15、0.20、0.25]中进行搜索，以达到最佳效果。

4.2. Results

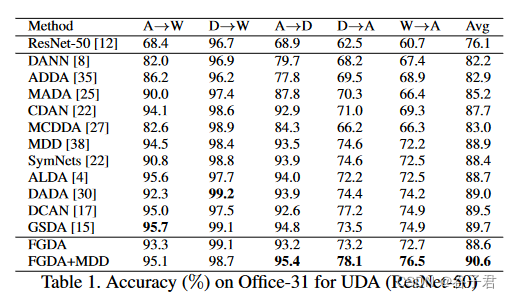
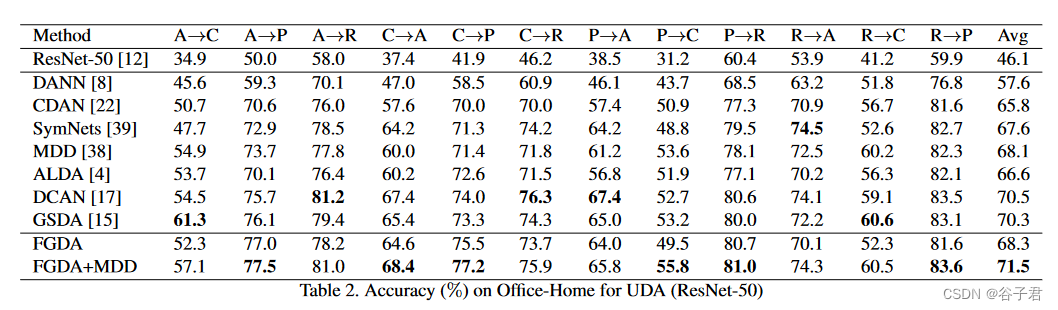
我们将所提出的方法与以前的一些ADA方法进行了比较。结果报告于表1和2。Office - 31上W→D的所有结果都是隐藏的，但是参与平均结果的计算，因为大多数模型在这个任务上达到了100 %。MADA [ 25 ]、CDAN [ 22 ]和GSDA [ 15 ]将单个或多个判别器作用于分类器输出以改进DANN [ 8 ]。SymNets [ 39 ]和DADA [ 30 ]通过依赖分类器输出和创造性的对抗学习机制进一步实现领域判别和混淆。MCDDA [ 27 ]和MDD [ 38 ]考虑了两个分类器的不一致以缓解类内分布差异。可以看出，FGDA取得了与MDD相媲美的结果，表明单独使用特征梯度对齐来减少分布差异是可行的。此外，FGDA + MDD在Office - 31数据集上和Office - Home数据集上分别比对比模型的最优结果提高了0.9 %和1.0 %

5. Further Analysis

5.1. Ablation Study

我们的研究从设置一个非适应模型作为第一条基线开始，该基线只需在源数据上微调RestNet - 50 [ 12 ]。为了证明我们的方法相对于基于表示的ADA方法的优势，DANN [ 8 ]，CDAN-E [ 22 ]和MDD [ 38 ]将分别与我们的方法结合并作为其他基线。为了研究高质量的伪标注如何提高性能，我们从我们的方法中删除了自监督伪标记( SPL )方法；为了检验梯度正则化的性能，我们还去掉了特征级的Jacobian正则化( FJR )；为了验证特征梯度对齐降低分布散度的可行性，我们同时去除FJR和SPL。为了观察损失函数的影响，当只应用特征梯度对齐时，将计算目标域梯度的损失函数由交叉熵改为条件熵最小化( Ent . )。
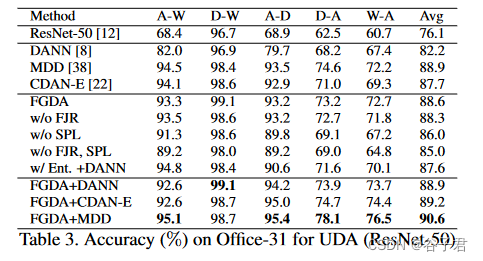
如表3所示，在相同的网络结构下，FGDA ( w / o FJR、SPL)比DANN有所改进，表明采用梯度作为表示不仅可以减少分布发散，而且可以得到更好的分布对齐效果。FGDA ( w / o FJR )和FGDA ( w / o SPL )能够显著提高FGDA ( w / o FJR、SPL)的性能，证明了各组分的有效性。同时，将FGDA ( w / Ent . )应用到DANN上，虽然没有FGDA + DANN的效果明显，但仍然获得了显著的性能增益。
对于FGDA，它的性能与MDD相当，并且大大优于DANN和CDAN。此外，当FGDA分别与DANN、CDAN - E和MDD结合时，结果证实了将梯度作为度量分布散度的表征单位化确实能够一致地提高基于表征的ADA。

5.2. Visualization Analysis

为了对FGDA有一个直观的认识，并表明梯度对齐确实有助于减少分布差异，我们使用tSNE [ 36 ]在Office - 31上可视化源域和目标域的特征及其梯度。如图5所示，在ResNet - 50 (仅源域)中，源域和目标域的特征分布和梯度分布由于域偏移较大而分布不同。当使用MDD对齐特征分布时，即使特征分布差异已经减小，梯度分布差异依然明显。相比之下，FGDA + MDD在特征和梯度的分布差异上都比MMD表现出更小的优势。此外，观察到目标特征与源特征一样具有判别性，在进行特征梯度对齐后，目标分布是类间分离和类内聚集的。注意，CDAN-E [ 22 ]、FGDA ( w / o FJR、SPL)和FGDA的可视化结果在补充文档中提供。

图5 . Office - 31任务A→W上仅源模型( Rest Net-50 )、MDD和FGDA + MDD的特征分布和梯度分布的t - SNE可视化。蓝色和红色点分别表示源域和目标域样本。

5.3. Sensitivity Analysis

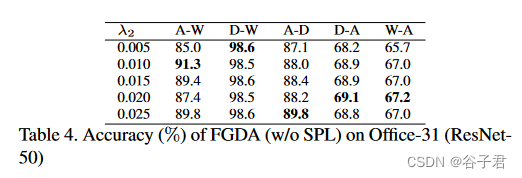
在表4中，我们实证了FGDA ( w / o SPL )中FJR的平衡参数λ 2的影响。从[ 0.05、0.10、0.15、0.20、0.25]中选取${\lambda }_2$，将Office - 31的所有结果呈现出来进行敏感性分析。虽然${\lambda }_2$的设定并没有一致的趋势，但我们观察到所选择的参数范围，从0.05到0.25，基本上可以涵盖大部分最好的结果。其他参数${\lambda }_1$和${\lambda }_3$的敏感性分析见补充文献。
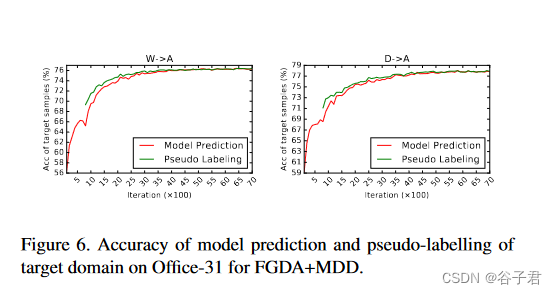
为了研究目标域中的伪标签噪声如何影响性能，在图6中对FGDA + MDD进行了案例分析。值得注意的是，FJR、SPL和MDD在900次迭代后得到应用。最初，即使没有高质量的伪标记，梯度对齐也是有效的。一旦涉及SPL，更精确的目标域梯度分布对性能有明显的促进作用。在使用梯度对齐进行训练时，获得了目标样本更加可分离的特征空间，使得伪标记和模型预测的准确率交替提高。因此，梯度对齐可以从伪标记中获益，反之亦然。除此之外，还有其他方法可以实现高质量的伪标注，如时间集成方法Mean教师模型[ 31 ]。

6. Conclusion

在这项工作中，我们表明现有的对抗域适应方法有一个固有的缺点，即即使判别器完全混淆，也不能保证两个分布之间有足够的相似性。针对这一问题，我们提出了一种新的特征梯度分布对齐方法，该方法能够进一步降低源域和目标域之间的分布差异。我们从理论和实证上证明了通过对齐特征梯度可以减小分布差异。更重要的是，我们提出的新框架在理论上保证了在目标域上可以获得比现有的对抗域自适应方法更严格的误差上界。大量的实验验证了我们提出的新框架可以在两个真实的基准数据上定量和定性地达到最新的性能。