Haar特征（一种矩形特征，反映了图像的灰度变化情况）

本文主要是介绍Haar特征（一种矩形特征，反映了图像的灰度变化情况），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

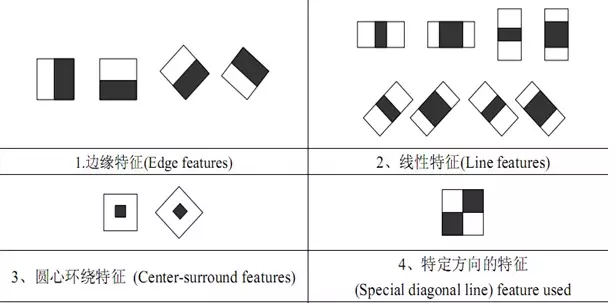
Haar特征最先由Paul Viola等人提出，后经过Rainer Lienhart等扩展引入45°倾斜特征。Haar特征分为三类：边缘特征、线性特征、中心特征和对角线特征，组合成特征模板。

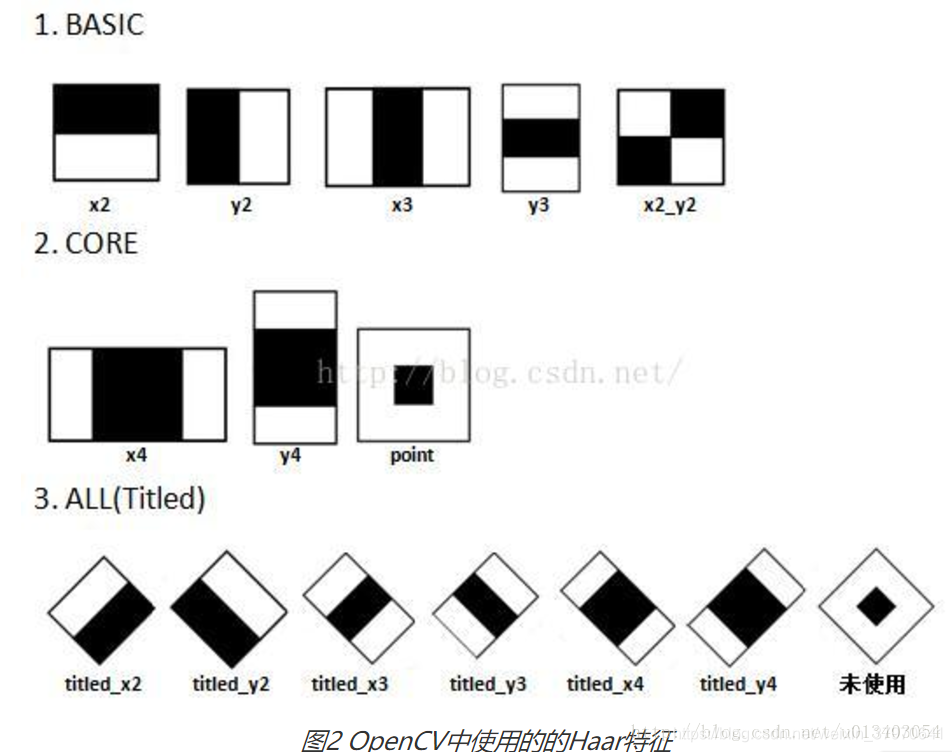
OpenCV（2.4.11版本）所使用的共计14种Haar特征，包括5种Basic特征、3种Core特征和6种Titled(即45°旋转)特征。在使用opencv自带的训练工具进行训练时，haarFeatureParams参数中的mode参数正对应了训练过程中所使用的特征集合:
1. 如果mode为BASIC，则只使用BASIC的5种Haar特征进行训练，训练出的分类器也只包含这5种特征。
2. 如果mode为CORE，则使用BASIC的5种+CORE的3种Haar特征进行训练。
3. 如果mode为ALL，则使用BASICA的5种+CORE的3种+ALL的6种Titled共14种特征进行训练。
默认使用BASIC模式，实际中训练和检测效果已经足够好。不建议使用ALL参数，引入Titled倾斜特征需要多计算一张倾斜积分图，会极大的降低训练和检测速度。

1、矩形特征模板的生成
haar特征模板内有白色和黑色两种矩形，模板的Haar特征值=白色矩形像素和减去黑色矩形像素和：
$featureValue(x)=weight_{white} * \sum_{Pixel\in White} Pixel+weight_{black}*\sum_{Pixel\in Blcak}Pixel$
设置权值就是为了抵消面积不等带来的影响，保证所有矩形Haar特征的特征值在灰度分布绝对均匀的图中为0:

a、对于上图中的x3和y3， $Weight_{White}=1$,$Weight_{Black}=-2$ ;
b、对于上图中的Point特征， $Weight_{White}=1$,$Weight_{Black}=-8$ ;
c、其余11种特征， $Weight_{White}=1$,$Weight_{Black}=-1$ ;
Haar特征值反映了图像的灰度变化情况。例如：脸部的一些特征能由矩形特征简单描述,如眼睛要比脸颊颜色要深，鼻梁两侧比鼻梁颜色要深，嘴巴比周围颜色要深等。但矩形特征只对一些简单的图形结构，如边缘、线段较敏感，所以只能描述特定走向（水平、垂直、对角）的结构。

2、Haar特征的子特征生成
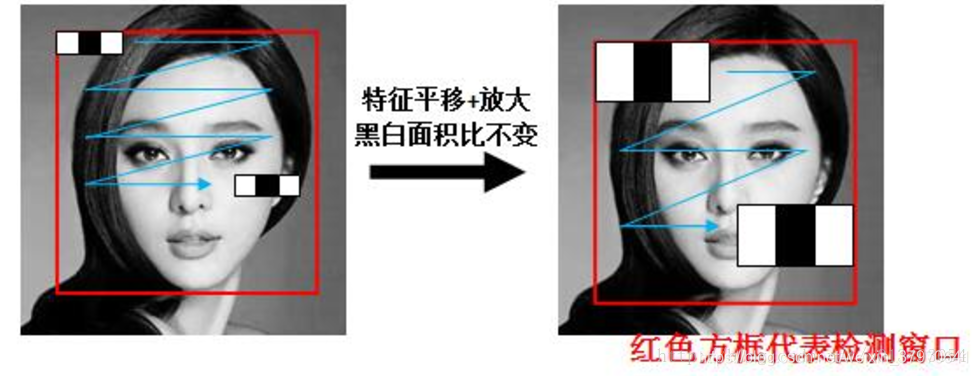
Haar特征矩形特征可位于图像任意位置，大小也可以任意改变，所以矩形特征值是矩形模版类别、矩形位置和矩形大小这三个因素的函数。故类别、大小和位置的变化，使得很小的检测窗口含有非常多的矩形特征，如：在24*24像素大小的检测窗口内矩形特征数量可以达到16万个(特定类别的矩形模板尺寸放缩时其黑白区域比例不变)。
以上图x3特征为例，在放大+平移过程中白：黑：白面积比始终是1:1:1。首先在红框所示的检测窗口中生成大小为3个像素的最小x3特征；之后分别沿着x和y平移产生了在检测窗口中不同位置的大量最小3像素x3特征；然后把最小x3特征分别沿着x和y放大(整数倍放大且保持黑白面积比例不变)，再平移，又产生了一系列大一点x3特征；然后继续放大和平移，重复此过程，直到放大后的x3和检测窗口一样大。这样x3就产生了完整的x3系列特征。

那么这些通过放大+平移的获得的子特征到底总共有多少个：
假设检测窗口大小为W*H，矩形特征大小为w*h，X和Y为表示矩形特征在水平和垂直方向的能放大的最大比例系数：

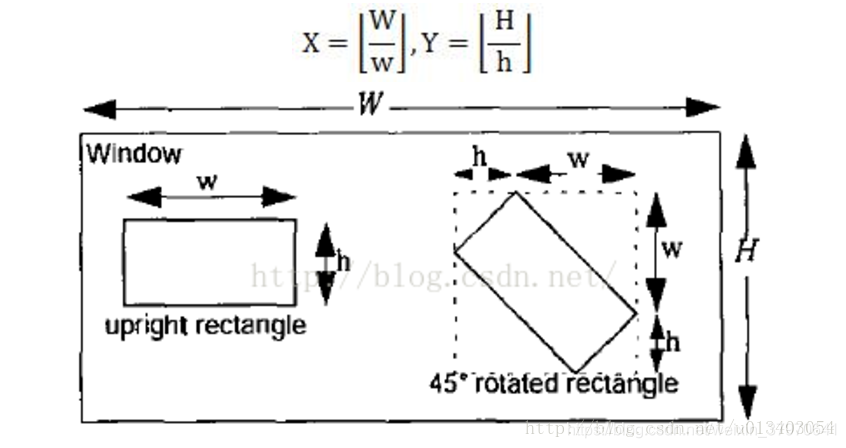
则总共可以获得的子特征数目为：

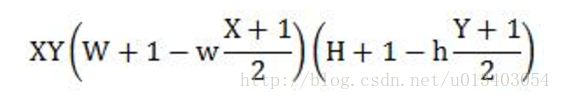
参数解释：
1、特征竖直方向方大1倍，即无放大，竖直方向有 $H-h+1$ 个特征;
2、特征竖直方向放大2倍，竖直方向有 $H-2h+1$ 个特征;
3、特征竖直方向放大3倍，竖直方向有 $H-3h+1$ 个特征;
4、特征竖直方向放大 $Y=floor(H/h)$ 倍，竖直方向有 $H-Y*h+1$ 个特征;
5、基于以上，竖直方向共有 $(H-h+1)+(H-2h+1)+(H-3h+1)+...+(H-Y*h+1)=Y[H+1-h(1+Y)/2]$ 个特征,同理水平方向： $X[W+1-w(1+X)/2]$ 个特征;

6、由于水平方向和垂直方向相互独立，所以子特征数目为：子特征数目 = 水平方向数目x垂直方向数目;

3、Haar特征值归一化(标准归一化也可以)

Haar特征计算出的特征值变化范围非常大，不利于量化评定特征值，所以需要进行“归一化”，压缩特征值范围。假设当前检测窗口中的图像像素为i(x,y),当前检测窗口为w*h大小，OpenCV采用如下方式归一化：
1、计算检测窗口中图像的灰度值和灰度值平方和：
$sum=\sum i(x,y)$
$sq_{sum}=\sum i^2(x,y)$
2、计算平均值：
$mean=\frac{sum}{w*h}$
$sq_{mean}=\frac{sq_{sum}}{w*h}$
3、计算归一化因子：
$varNormFactor=\sqrt{sq_{mean}-mean^2}$
4、归一化特征值：
$normValue=\frac{featureValue}{varNormFactor}$

4、Haar-like特征计算-积分图----滑窗默认步长为1

积分图就是只遍历一次图像就可以求出图像中所有区域像素和的快速算法，大大的提高了图像特征值计算的效率。对于一个灰度图像I而言，其积分图也是一张与I尺寸相同的图，只不过该图上任意一点(x,y)的值是指从灰度图像I的左上角与当前点所围成的举行区域内所有像素点灰度值之和,类似于图像直方图与图像累积直方图的关系，这里只不过是二维的图像。

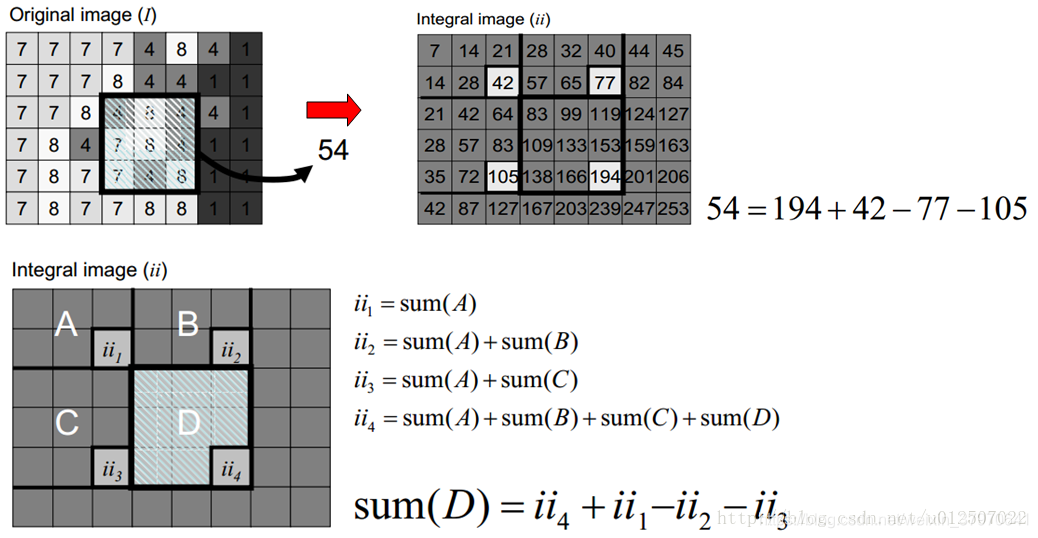
当把图像扫描一遍，到达图像右下角像素时，积分图像就构造好了。积分图构造好之后，图像中任何矩阵区域的像素累加和都可以通过简单运算得到如上图所示。而Haar-like特征值无非就是两个或三个矩阵像素和的差，同样可以在常数时间内完成。所以矩形特征的特征值计算，只与此特征矩形的端点的积分图有关，所以不管此特征矩形的尺度变换如何，特征值的计算所消耗的时间都是常量。这样只要遍历图像一次，就可以求得所有子窗口的特征值。

5、45°旋转积分图
基于点90°夹角的射线与原图左上角包围的像素和构成旋转积分图：

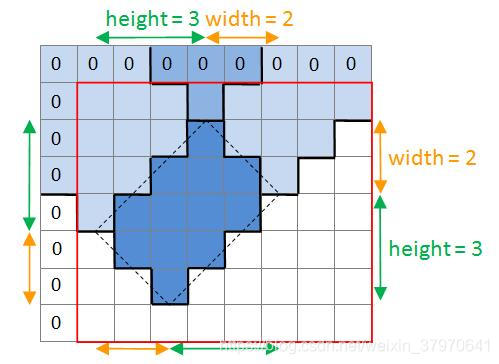
设有如下图红色方框大小的灰度图image，其计算出来的45°旋转灰度图为titled（第1行和第1列为0），虚线代表image中cv::Rect为<3 1 2 3>区域。显然虚线区域的灰度和为：titled(2,6) - titled(1,4) - titled(6,3) + titled(1,4):